二次函数
http://www.newdu.com 2025/12/10 09:12:18 中考网 佚名 参加讨论
1.如果自变量的取值是全体实数,那么二次函数在图象顶点处取到最大值(或最小值)。 这时有两种方法求最值:一种是利用顶点坐标公式,一种是利用配方计算。 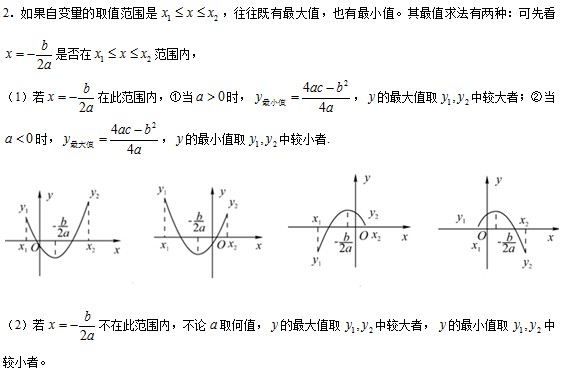 二、二次函数与一元二次方程、二次三项式的关系 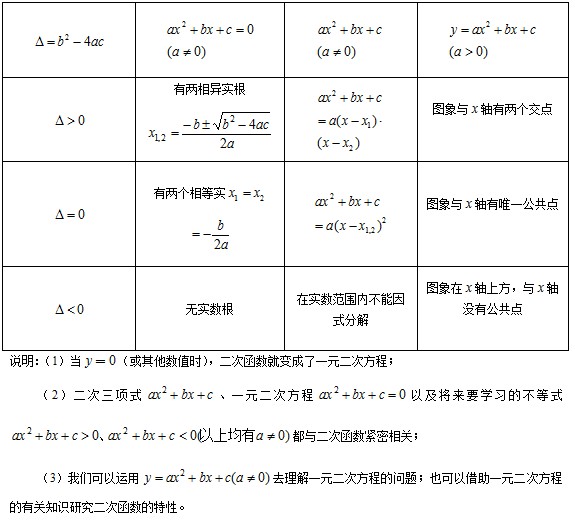 三、二次函数的实际应用 在公路、桥梁、隧道、城市建设等很多方面都有抛物线型;生产和生活中,有很多“利润最大”、“用料最少”、“开支最节约”、“线路最短”、“面积最大”等问题,它们都有可能用到二次函数关系,用到二次函数的最值。 那么解决这类问题的一般步骤是: 第一步:设自变量; 第二步:建立函数解析式; 第三步:确定自变量取值范围; 第四步:根据顶点坐标公式或配方法求出最值(在自变量的取值范围内)。 常见考法 (1)考查一些带约束条件的二次函数最值; (2)结合二次函数考查一些创新问题。 二次函数顶点式、交点市、两根式 一般地,自变量x和因变量y之间存在如下关系: (1)一般式:y=ax2+bx+c (a,b,c为常数,a≠0),则称y为x的二次函数。顶点坐标(-b/2a,(4ac-b^2)/4a) (2)顶点式:y=a(x-h)2+k或y=a(x+m)^2+k(a,h,k为常数,a≠0). (3)交点式(与x轴):y=a(x-x1)(x-x2) (4)两根式:y=a(x-x1)(x-x2),其中x1,x2是抛物线与x轴的交点的横坐标,即一元二次方程ax2+bx+c=0的两个根,a≠0. 说明: (1)任何一个二次函数通过配方都可以化为顶点式y=a(x-h)2+k,抛物线的顶点坐标是(h,k),h=0时,抛物线y=ax2+k的顶点在y轴上;当k=0时,抛物线a(x-h)2的顶点在x轴上;当h=0且k=0时,抛物线y=ax2的顶点在原点. (2)当抛物线y=ax2+bx+c与x轴有交点时,即对应二次方程ax2+bx+c=0有实数根x1和x2存在时,根据二次三项式的分解公式ax2+bx+c=a(x-x1)(x-x2),二次函数y=ax2+bx+c可转化为两根式y=a(x-x1)(x-x2). 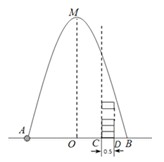 误区提醒 (1)忽略自变量的取值范围,所求最值不符合实际意义; (2)二次函数的坐标系建立的不恰当,给解题带来了困难。 新初三快扫码关注 中考网微信公众号 每日推送学习技巧,学科知识点 助你迎接2020年中考!  三、二次函数的实际应用 在公路、桥梁、隧道、城市建设等很多方面都有抛物线型;生产和生活中,有很多“利润最大”、“用料最少”、“开支最节约”、“线路最短”、“面积最大”等问题,它们都有可能用到二次函数关系,用到二次函数的最值。 那么解决这类问题的一般步骤是: 第一步:设自变量; 第二步:建立函数解析式; 第三步:确定自变量取值范围; 第四步:根据顶点坐标公式或配方法求出最值(在自变量的取值范围内)。 常见考法 (1)考查一些带约束条件的二次函数最值; (2)结合二次函数考查一些创新问题。 二次函数顶点式、交点市、两根式 一般地,自变量x和因变量y之间存在如下关系: (1)一般式:y=ax2+bx+c (a,b,c为常数,a≠0),则称y为x的二次函数。顶点坐标(-b/2a,(4ac-b^2)/4a) (2)顶点式:y=a(x-h)2+k或y=a(x+m)^2+k(a,h,k为常数,a≠0). (3)交点式(与x轴):y=a(x-x1)(x-x2) (4)两根式:y=a(x-x1)(x-x2),其中x1,x2是抛物线与x轴的交点的横坐标,即一元二次方程ax2+bx+c=0的两个根,a≠0. 说明: (1)任何一个二次函数通过配方都可以化为顶点式y=a(x-h)2+k,抛物线的顶点坐标是(h,k),h=0时,抛物线y=ax2+k的顶点在y轴上;当k=0时,抛物线a(x-h)2的顶点在x轴上;当h=0且k=0时,抛物线y=ax2的顶点在原点. (2)当抛物线y=ax2+bx+c与x轴有交点时,即对应二次方程ax2+bx+c=0有实数根x1和x2存在时,根据二次三项式的分解公式ax2+bx+c=a(x-x1)(x-x2),二次函数y=ax2+bx+c可转化为两根式y=a(x-x1)(x-x2). 二次5.jpg 误区提醒 (1)忽略自变量的取值范围,所求最值不符合实际意义; (2)二次函数的坐标系建立的不恰当,给解题带来了困难。 (责任编辑:admin) |
- 上一篇:二次函数与一元二次方程、二次三项式的关系
- 下一篇:初中数学二次函数知识点汇总(1)