2012年数学学习方法:四边形知识解读
http://www.newdu.com 2025/12/13 04:12:26 互联网 佚名 参加讨论
一、主要知识点 1、平行四边形的性质和判定 (1)平行四边形的性质:①对边平行;②对边相等;③对角相等、邻角互补;④对角线互相平分;⑤中心对称图形(两条对角线的交点是对称中心)。 (2)平行四边形的判定:①两组对边分别平行的四边形;②两组对边分别相等的四边形;③一级对边平行且相等的四边形;④两组对角分别相等的四边形;⑤对角线互相平分的四边形。 2、特殊平行四边形的性质和判定 表1
3、特殊平行四边形与平行四边形的关系 平行四边形、矩形、菱形、正方形之间的关系如图1所示。 二、例题讲解 例1 如图2,在ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB。 (1)试证明:四边形AFCE是平行四边形。 (2)若去掉条件“∠DAB=60°”,(1)的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由。 思路分析:(1)由条件可知EC∥AF,要证四边形AFCE是平行四边形,只需证明EC=AF即可。即只需证明ED=BF。而利用条件可证明△AED、△CFB都是等边三角形,从而命题得证。(2)要探讨四边形AFCE是否仍然是平行四边形,只需使用(1)中的解决办法,但在证明ED=BF时,必须证明它们所在的三角形全等。 解:(1)因为四边形ABCD是平行四边形,所以AB∥CD,∠DCB=∠DAB=60°,所以∠ADE=∠CBF=60°。 因AE=AD,CF=CB,故△AED和△CFB都是等边三角形。因EC=CD+DE=CD+AD,AF=AB+BF=AB+BC,故EC=AF。 又AB∥CD,故EC∥AF,所以四边形AFCE是平行四边形。 (2)上述结论依然成立,证明如下: ∵AE=AD,CF=CB,∴∠AED=∠ADE,∠CFB=∠CBF。 又∵∠ADE=∠DAB=∠BCD=∠CBF。 ∴∠AED=∠CFB。 又∵AD=BC,∴△ADE≌△CBF(AAS)。ED=FB。 下同(1),四边形AFCE是平行四边形。 方法规律:要证明一个四边形是平行四边形,方法有五种,要结合题设,做出恰当选择。本题中已有一组对边平行,那么只需要再证明这一组对边相等即可(证明另一组对边平行也可以,但难度较大)。 例2 如图3,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=DF。 (1)若四边形AECF是平行四边形,试证明:四边形ABCD是平行四边形. (2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么? (3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由。 思路分析:由于点E、F都在四边形ABCD的对角线上,且“BE=DF”这个条件也与对角线BD有关,故考虑从对角线的角度去判断四边形ABCD的形状。 解:(1)因为AO=CO,EO=FO,BE=DF,所以BE+EO=DF+FO,即BO=DO,所以四边形ABCD为平行四边形. (2)因为AECF是菱形,所以AC⊥BD. 又由(1)知,四边形ABCD是平行四边形,所以四边形ABCD是菱形. (3)四边形ABCD不是矩形(因为尽管四边形AECF的对角线相等,但四边形ABCD的对角线显然就不相等了). 方法规律:本题设置的三个小问题,考查了平行四边形、矩形、菱形的判定和性质.这些特殊四边形的判定方法和性质都可以从边、角、对角线考虑,因而证明方法也不唯一.比如,也可证明△AFD≌△CEB(SAS),△ABE≌△CDF(SAS)。 三、考题演练 1、下列命题中的假命题是。 A、一组邻边相等的平行四边形是菱形 B、一组邻边相等的矩形是正方形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边相等且有一个角是直角的四边形是矩形 2、如图4,已知正方形ABCD的边长为2,△BPC是等边三角形,则△CDP的面积是 ,△BPD的面积是 。 3、如图5,在四边形ABCD中,E、F、G、H分别是且AB、BD、CD、AC的中点.要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 。 4、如图6,在ABCD中,AE、BF分别平分∠DAB和∠ABC,且分别交CD于点E、F。AE、BF相交于点M。 (1)试说明AE⊥BF。 (2)判断线段DF与CE的大小关系,并予以说明。 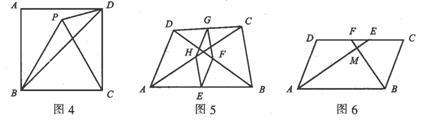 参考答案 |