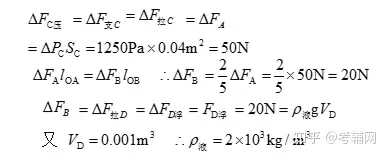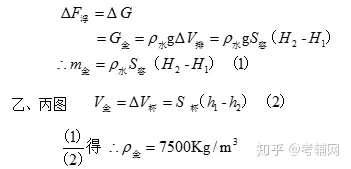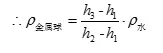一、浮体
浮体综合题的解题思路和方法:
(1)先明确物体在液体中的状态:漂浮。
(2)分析物体的受力情况:只受到重力G物和浮力F浮两个力的作用,并处于静止状态。
(3)列出二力平衡的方程:F浮 = G物 。
(4)展开求解:将求浮力的公式F浮 = ρ液 gV排、重力公式G物=m物g(或 G物=ρ物 V物g)求未知量。
1.漂浮体
例1一个木块浮在水面上,它浸入水中的体积是总体积的四分之三;将这个木块放在某种液体中,它也浮在液面上,并且露出液面的体积是总体积的五分之二。求:
(1)这个木块的密度;
(2)液体的密度。
提示:(1)利用木块漂浮,F浮 = G物 ,
ρ水V排g=ρ物V物g ,
ρ物 = (3 / 4)ρ水= 0.75×103kg / m3 。
(2)利用F液浮 = F水浮 = G物 ,
∴ρ液V液排g =ρ水V水排g
∴ ρ液 = (5 / 4)ρ水= 1.25×103kg / m3 。
答案:(1)木块的密度是 0.75×103kg / m3。
(2)液体的密度是 1.25×103kg/m3 。
http://weixin.qq.com/r/cyjp8RjE4kWdrVyS931h(二维码自动识别)

变式1一木块漂浮在水面上,它露出液面的体积是24cm3 。把木块露出液面的体积切去,将剩余部分再放入水中,静止时木块又有18cm3的体积露出液面。这个木块的密度是多大?
提示:根据浮沉条件利用两个等式F′=G+ G′,F浮=G展开解题。
答案:ρ木=0.75×103kg/ m3 。
例2边长为1dm的正立方体木块,漂浮在酒精液面上,有一半的体积露出液面,如图甲所示,将木块从底部去掉一部分,粘上体积相同的玻璃后,投入某种液体中,它仍漂浮,如图乙所示,此时液体对它竖直向上的压强为980Pa,酒精和玻璃的密度分别为ρ酒精=0.8×103kg/m3,ρ玻璃=2.4×103kg/m3,胶的质量和体积忽略不计,求:
(1)木块的密度
(2)玻璃的质量
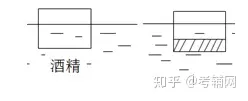
提示:(1)F浮=G木
ρ木=0.4×103kg/ m3 。
(2)F浮′= G剩木+ G玻
ρ液gV排= ρ木gV排剩木+ ρ玻gV玻
P下S下= ρ木g(V木-V玻)+ ρ玻gV玻
m玻= ρ玻V玻
m玻=0.72kg
例3欢欢利用小试管、螺母和细线制成一个“土密度计”,用如图所示的方法测量液体的密度。“土密度计”在酒精(ρ酒精=0.8×103kg/m3)中静止时露出液面的高度为2cm; “土密度计”在水中静止时露出液面的高度为3cm;“土密度计”在硫酸铜溶液中静止时露出液面的高度为3.8cm。则此硫酸铜溶液的密度为________kg/m3。
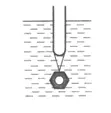
提示:利用F酒浮=F水浮 =F酸浮
答案:1.25×108
2.浮体载物问题
(1)浮体上压一物体;
(2)浮体下挂一物体;
(3)筒内载有物体。
方法:将整个装置看作一个整体,按浮体处理。
注意:物体受到的浮力情况,弄清物体的排液体积。
例1一木块放在水中静止时,有54cm3的体积露出水面,如图1所示。现将一体积为20cm3的金属块放在木块的上面,木块恰好全部浸在水中,如图2所示.求:金属块的密度。

分析:涉及到有两个状态的浮体浮力题。
第一个状态如图1:以木块为研究对象,木块漂浮,F浮 = G木;
第二个状态如图2:以木块和金属块整体为研究对象,漂浮在水面上,F浮’ = G木 +G金。
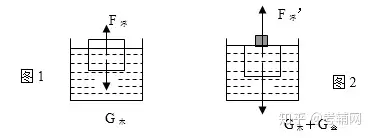
比较第二个状态和第一个状态,即: ΔF浮= G金 ,代入浮力和重力公式后:ρ水 g ΔV排=ρ金 g V金
ΔV排=V露 ,则:ρ金=ρ水V露/V金=(5.4×10—5m3 ×1.0×103 Kg / m3 )/(2×10—5m3)=2.7×103 Kg / m3 。
例2如图所示,装有石块的小船浮在水面上时所受的浮力为F1 ,把石块卸入水中后,石块受到的浮力为F2 ,池底对石块的支持力为N 。这时( )
A. 空船受到的浮力为F1—F2—N
B. 石块受到的重力为F1—F2
C. 石块受到的支持力N = F1—F2
D. 船排水体积减小了(N+F2)/ρ水g
答案:A D
练习:
1.一根均匀的木棍长度为L,密度为ρ1。下端挂一个质量为m的小金属块后,能如图所示漂浮在密度为ρ2的液体中。此时木棍露出液面的长度为h。用剪刀剪掉长度为L'=_________的木棍,剩余的木棍和金属块恰能悬浮在原来的液体中。
答案:ρ2h/(ρ2-ρ1)
2.如图所示,一个由均匀材料组成的实心圆柱体,底面积为S,将它放入水中,静止后呈竖直漂浮状态,其体积的1/2露出水面。若在圆柱体下底面帖一层厚度为d、面积也为S的均质塑料(胶的质量和厚度均不计),再把它放入水中,仍能竖直漂浮于水中面,但露出水面的高度减小了h,求塑料的密度。
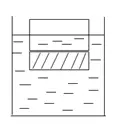
答案:ρ塑=(d+h)/d×ρ水
3.一个土密度计如图8所示,其刻度部分的A、B 、C三点,AB=2cm,AC=6cm。将密度计放在酒精(ρ酒精=0.8×103kg/m3)中时,液面位置恰好在A点,将密度计放在水中时,液面位置恰好在B点,当密度计放在某种液体中时,液面位置恰好在C点,则这种液体的密度是_______ kg/m3。
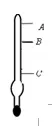
答案:2×103
二、三力平衡
例1如图所示,木块用细绳系在容器的底
部,向容器内注入水,当木块的一半体积浸在水中时,绳对木块的拉力是5N;当木块浸没在水中时,绳对木块的拉力是30N。求:
(1)木块的密度;
(2)木块的体积。(g = 10N / Kg)
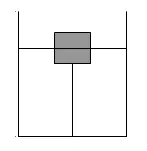
分析:木块在水中,它在两种情况下受力的示意图见下图所示。
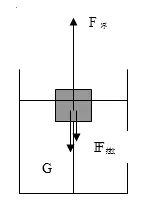
可以列出下面的两个方程:
F拉 = F浮 — G -------- (1)
F拉 ’= F浮 ’— G -------- (2)
木块的密度为:ρ木 = 0.4×103 kg / m3 。
木块的体积为:V木 = 5×10—3m3 。
解题技巧:
在列出两个力的平衡方程以后:
① 利用两式相减,可以约去相同项。
② 利用两式相比,可以约去相同量。简化计算过程
注意:提升水中的物体受力变化
ΔF拉=ΔF浮=ΔF液压底
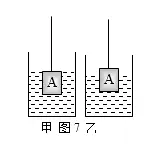
例2如图7甲所示,底面积为50cm2的圆柱形玻璃筒中装有一定量的水,放在水平台面上,底面积为10cm2的圆柱形物体A浸没在水中, 细绳对物体的拉力为F拉。如图7乙所示,当物体A有的体积露出水面时,作用在物体A上的竖直向上的拉力为4N,筒中水的深度比图7甲中水的深度下降了0.4 cm,此时,物体A所受的浮力为F浮,水在物体A底面处产生的压强为p。g取10N/kg,悬挂物体的细绳的质量忽略不计。
A. F拉的大小为4.8N B. F浮的大小为0.2N
C. ρA的大小为8g/cm3 D. p的大小为300Pa
提示:

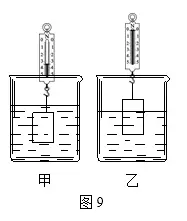
变式1底面积为100cm2的烧杯中装有适量水。当金属块浸没在水中静止时,如图9甲所示,弹簧测力计的示数F1=3.4N,水对杯底的压强为p1;当金属块总体积的1/4露出水面静止时,如图9乙所示,弹簧测力计的示数为F2,水对杯底的压强为p2;若p1、p2之差为50Pa,g取10N/kg,则
A.金属块的体积V金是2×10-3m3
B.弹簧测力计的示数F2是5.4N
C.金属块的密度是2.7×103kg/m3
D.金属块受到的重力是6.8 N
答案:C
三、浮力与杠杆、滑轮综合
杠杆两端受力的变化(力臂的比不变)
ΔF1·lOA=ΔF2·lOB
例3如图8所示,杠杆AB的A点挂边长为2dm、密度为ρ1=2kg/dm3的正方体C,B点挂边长为1dm正方体D,AO:OB=2:5,杠杆在水平位置平衡时,D静止在空中,C对水平地面的压强为p1=1000Pa;若将正方体D浸没在某种液体中(未接触到容器底),杠杆在水平位置平衡时,C对水平地面的压强增大了1250Pa,取g=10N/kg,可求得( )
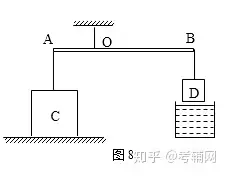
A.物块D的密度为5kg/dm3
B.液体的密度为2kg/dm3
C.当物体D浸没在液体中时A点所受竖直向下的拉力为95N
D.若物体D不浸入液体,要使物体C对地面的压强为零,则应对物体D施加竖直向下的64N的力
提示:
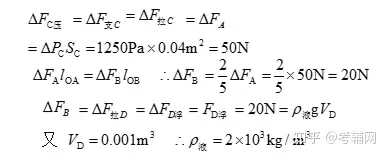
答案:B
例4如图8甲所示的装置处于静止状态,底面积为60cm2的圆柱形玻璃筒中装有适量的水,放在水平台面上,质量为800g的圆柱形物体B浸没在水中,此时水对容器底的压强是2500 Pa,物体A是体积为50cm3的圆柱体配重。如图8 乙所示,当用力F竖直向下拉物体A时,物体B有的体积露出水面且静止,此时滑轮组提升重物B的机械效率为80%,水对容器底的压强为2100 Pa。 g取10N/kg,悬挂物体的细绳的质量以及绳与轮间的摩擦忽略不计,物体A的密度是______kg/m3。
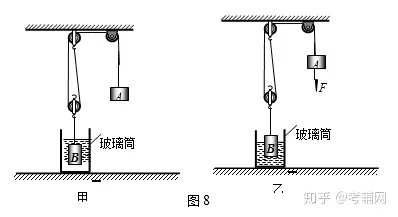
答案:3.1×103
练习:
1.如图所示的木块浸没在水中,细线对木块的拉力是2N。剪断细线,待木块静止后,将木块露出水面的部分切去,再在剩余的木块上加1N向下的压力时,木块有20cm3的体积露出水面,则木块的密度约为______kg/m3。(g取10N/kg)
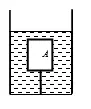
答案:0.6×103
2.底面积为50cm2的平底圆柱形容器内盛满某种液体后,放置于水平桌面的中央(容器壁厚度不计),已知液体的压强与深度的关系如图10所示。现用轻质细线提起一个质量为80g的实心球缓慢浸没于容器内的液体中,如图11所示,待球静止后,擦干容器外壁,已知细线给球的拉力为0.5N,剪断细线,实心球下沉到容器底部,此时容器对桌面的压强比只盛满液体容器对桌面的压强增大了_____pa.
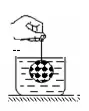
答案:100
3.如图10所示,顶面带有光滑凹槽的轻质杠杆AB可以绕支点O转动,杠杆的A端用细线沿竖直方向连接在地板上,OB=0.5m,在杠杆的B端悬挂一个密度为0.8×103kg/m3的圆柱体M。地板上有一个盛满水的容器。在圆柱体M体积的1/3浸入水中时,从容器内溢出0.4N的水,杠杆在水平位置平衡。此时让一个质量为200g的小球从B点沿凹槽向A端匀速运动,经过4s的时间,系在A端细线的拉力恰好等于0N。若整个过程中杠杆始终保持水平平衡,则小球的运动速度为________m/s。(g取10N/kg)
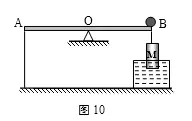
答案:0.16
4.如图所示,某圆柱形容器装有适量的水,底面积为20cm2,将物体B放入水中时,通过磅秤测得总质量150g;使用一个杠杆提起物体B,发现当杠杆C端挂钩码A时,杠杆在水平位置恰好平衡,物体B刚好有一半体积露出水面。此时天平示数为70g。测得容器内液面下降了1cm。则物体B的密度为___kg/m3。( g取10N/kg)
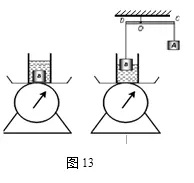
答案:2.5×103
四、液面变化、浮力与压强综合
“柱形”容器装液体时
ΔF液压底=ΔF浮= ΔPs
V球=S容器Δh容
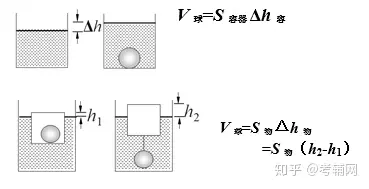
例1小阳想测出一块鹅卵石的密度。他在家中利用刻度尺、口大底小的塑料碗、大烧杯和适量的水进行实验,在烧杯内放入适量水,再将塑料碗轻轻放入水中漂浮,如图甲所示。用刻度尺测出此时水盆内水的深度为h1。将鹅卵石放在塑料碗中,装有鹅卵石的塑料碗仍在水中漂浮,如图乙所示。用刻度尺测出此时水盆内水的深度为h2,将塑料碗中的鹅卵石放入水盆中,如图丙所示。用刻度尺测出此时水盆内水的深度为h3,求ρ石=_______。
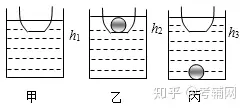
答案:(h2-h1)/( h3-h1)
例2圆柱形容器中装有适量的水,将一只装有配重的薄壁长烧杯放入圆柱形容器的水中,烧杯静止时容器中水的深度H1为20cm,如图15甲所示。将金属块A吊在烧杯底部,烧杯静止时露出水面的高度h1为5cm,容器中水的深度H2为35cm,如图15乙所示。将金属块A放在烧杯中,烧杯静止时露出水面的高度h2为1cm,如图15丙所示。已知圆柱形容器底面积为烧杯底面积的2倍。则金属块A的密度为____kg/m3。
提示:
甲 乙图
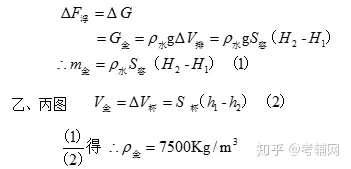
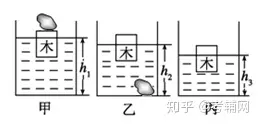
例3如图11甲所示;一个底面积为50 cm2的烧杯装有某种液体,把小石块放在木块上,静止时液体深h1=16cm;如图11乙所示;若将小石块放入液体中,液体深h2=12 cm,石块对杯底的压力F=1.6N;如图11丙所示,取出小石块后, 液体深h3=10cm。则小石块的密度ρ石为_____kg/m3。(g取10N/kg)
练习:
1.如图12所示,质量为540g的凹形铝槽,放入底面积为100cm2的圆柱形液体中,铝槽浮在液面上,槽口恰好与液面相平,这时液面上升了2.7cm,若使铝槽沉入液体中,则沉入前后液体对容器底部的压强变化△P=________Pa。(已知ρ铝=2.7×103 kg/m3 g=10N/kg)
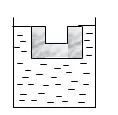
答案:140
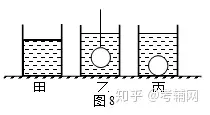
2.如图11所示,边长为L的正方体空心金属盒和实心金属球各一个。若把球放在盒内密封后,放入密度为ρ的液体中金属盒有h1的高度露出液面,如图8甲所示;若把球和盒用细绳相连放入液体中静止后,金属盒有h2的高度露出液面,如图8乙所示;若把球和盒分别放入液体中静止后,金属盒有h3的高度露出液面,金属球沉入液体底部,如图8丙所示。不计细线的重力和体积。金属球的密度 ρ球=_______。
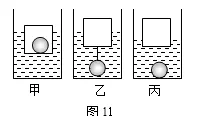
答案:
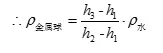
3.盛有液体的圆柱形容器置于水平桌面上,如图8甲所示,容器对桌面的压强为500Pa;用细线拴一金属球,将金属球浸没在液体中,如图8乙所示,容器对桌面的压强为600Pa;将细线剪断,金属球沉到容器底部,如图8丙所示,容器对桌面的压强为1500Pa。已知:容器的底面积为100cm2,金属球的密度为8g/cm3,g取10N/kg。则下列判断正确的是
A.金属球所受浮力是6N
B.金属球的体积是100cm3
C.液体的密度是0.8 g/cm3
D.金属球对容器底部的压力是10N
答案:C
(责任编辑:admin)
|