
典型例题
【例1】如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是( )
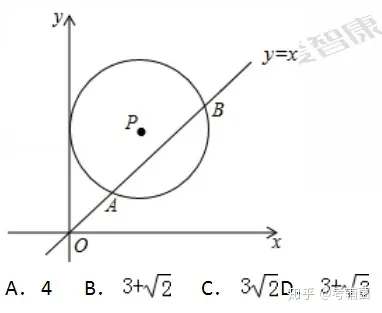
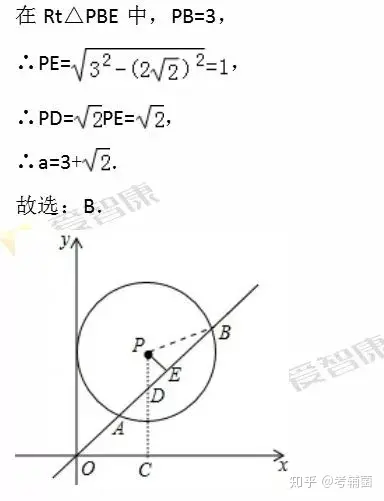
【分析】本题考查的是圆的垂径定理,同时也考查了勾股定理和等腰直角三角形的性质.我们可以做PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=3,PC=a,求得D点坐标,判断△OCD,△PED的形状.由PE⊥AB,根据垂径定理得AE=BE=AB=2,在Rt△PBE中,利用勾股定理可计算出结果。
答案

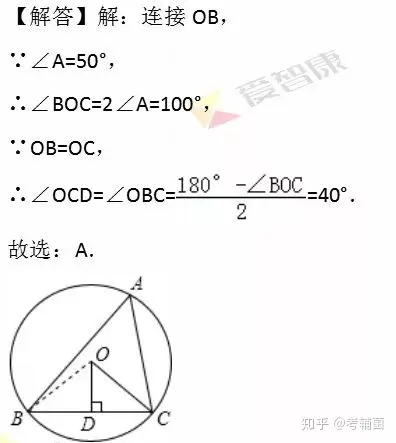
【例2】如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠OCD的度数是( )
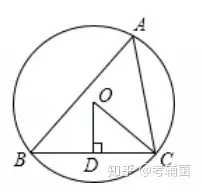
A.40° B.45° C.50° D.60°
【分析】此题考查了圆周角定理与等腰三角形的性质.难度不大,需要注意掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用。首先连接OB,由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BOC的度数,又由OB=OC,根据等边对等角的性质,即可求得∠OCD的度数.
答案
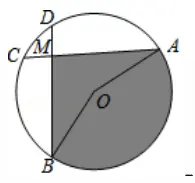
【例3】(2016秋•杭州期末)如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B
(1)求证:AC=BD;
(2)若OA=4,∠A=30°,当AC⊥BD时,求:
①弧CD的长;
②图中阴影部分面积.
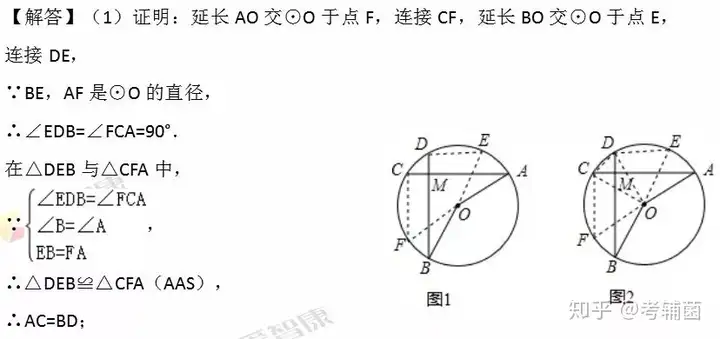
【分析】这道题目考查的是垂径定理,扇形面积的计算,以及全等三角形的判断和性质,我们需要根据题意作出辅助线,构造出直角三角形是解答此题的关键.第一问可以延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,根据圆周角定理得出∠EDB=∠FCA=90°,故可得出△DEB≌△CFA,由此得出结论;
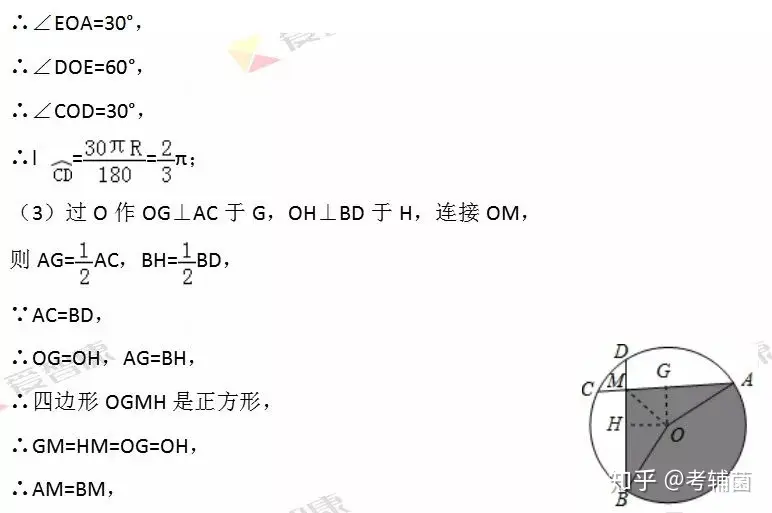
第二问第一小问延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,求出∠COA的度数,再由三角形外角的性质得出∠EOA的度数,由弧长公式即可得出结论;第二小问过O作OG⊥AC于G,OH⊥BD于H,连接OM,根据垂径定理得到AG=AC,BH=BD,推出四边形OGMH是正方形,根据正方形的性质得到GM=HM=OG=OH,得到AM=BM,解直角三角形得到相关长度,根据全等三角形的性质得到∠B,求得∠AOB度数,得到结果.
答案


变式练习
【练习1】如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E,GB=8cm,AG=1cm,DE=2cm,则EF= cm.
【练习2】如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD= 度.
【练习3】如图,CD是⊙O的直径,弦AB⊥CD,垂足为点M,AB=20,分别以CM、DM为直径作两个大小不同的⊙O1和⊙O2,则图中阴影部分的面积为 (结果保留π).
【练习4】如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=.
答案
【练习1】6
【练习2】38
【练习3】50π
(责任编辑:admin)
|