|
基于《课程标准》的数学学业考试要点剖析五 二、关于“数学思考”的考查 作为一个课程目标领域,“数学思考”的学习一直是结合知识、技能的学习进行的。对它的考查自然也是这样进行。具体内容包括: 在面临各种问题情境时,能够从数学的角度去思考问题,能够发现其中所存在的数学现象并运用数学的知识与方法去解决问题。我们应特别关注学生在数感、符号感、空间观念、统计观念、应用意识、推理能力等方面的发展情况,在考试中主要体现在以下方面: 1. 运用数学符号和图形描述现实世界,具有初步的数感、符号感和抽象思维能力。 这一目标主要包括能够在较复杂的层面上用数字和图表刻画现实生活中的现象,对一些数字信息作出合理解释与推断,并运用代数中的方程、不等式、函数等去刻画具体问题,建立合适的数学模型。 2. 对现实空间及图形有较丰富的认识,具有初步的空间观念和形象思维能力。 这一目标主要包括能够通过动手操作、图形变换等多种方式探索图形的形状、大小、位置关系、等量关系等,进行简单的图案设计、构建几何空间,并尝试用图形去从事推理活动。 3. 能运用数据描述信息,作出合理推断,具有统计的观念。 这一目标主要包括能够从事较为完整的统计活动,能针对现实情景中呈现的原始数据,并根据需要进行重新整理和分析,对数据作数学处理,按照处理的结果做出合理推断与决策。同时了解在现实情境中收集与表达数据的基本方法,能够运用计算器或计算机来处理较为复杂的数据。 4. 能够通过观察、实验、猜想、证明等数学活动过程,作出合情推理和演译推理,能有条理地、清晰地阐述自己的观点。 这一目标主要包括能够通过推理作出合理的判断与选择,尝试通过不同的方式去检验一个猜想的可信性,通过不同类型的推理活动形成一个合乎情理的猜想,并能够用比较规范的逻辑推理形式表达自己的演译推理过程。 例32 用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转. (1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图13—1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论; (2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13—2),你在(1)中得到的结论还成立吗?简要说明理由. 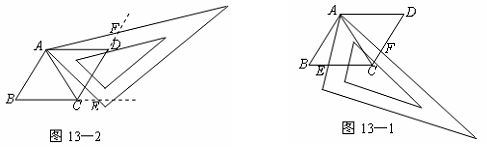 考查内容:观察动态变化过程中存在的恒定等量关系,并能够进行必要的归纳和验证。能否将前面经历的数学活动中蕴涵的知识和方法以类比的方式运用到新的情境中去,从而提出新猜想,解决新问题。 例33 为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验, 每人打10发子弹,下面是甲、乙两人各自的射击情况记录(其中乙的情况记录表上射中9、10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9、10环的子弹数均不为0发): 甲: 乙: 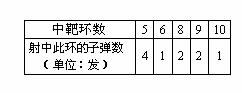 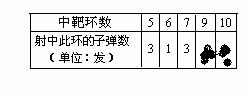 (1)求甲同学在这次测验中平均每次射中的环数; (2) 根据这次测验的情况,如果你是教练,你认为选谁参加比赛比较合适,并说明理由(结果保留到小数点后第1位). 考查内容:处理数据并根据结果形成自己的合理看法,作出相应的推断和决策。 例34 我们在学习勾股定理时构造了下面的模型:⊿ABC是直角三角形,其中∠C是直角,分别以Rt⊿ABC的三边为边向外作三个正方形,面积分别用S1,S2,S3表示,那么我们有:S1=S2+S3。 (1) 如果我们分别以Rt⊿ABC的三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明。 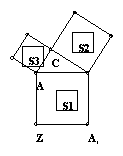 (2) 小明说,如果分别以Rt⊿ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为了使S1,S2,S3之间仍然具有上述关系,所作三角形应当具有相似的关系,你认为他的说法对吗? (3) 你能构造一个模型,即以Rt⊿ABC三边为边向外作三个图形,使得三个图形的面积具有上述关系吗?具体做一做。 考查内容:类比能力(第一问从题目中的正方形类比到正三角形,要求学生对结论进行类比);构造模型解释现象(在对第二问提供的信息“相似”有充分的理解基础上,回答第三问)。 例35 (1)用一条直线可以将一个正方形分成两个全等的部分,如下图。将正方形分成两个全等的图形的直线还有很多,试在图上另作出两条以上这样的直线。  (2)将圆分成两个全等图形的直线有多少条,试在图上作出几条这样的直线。 (3)将长方形分成两个全等图形的直线又有多少条呢?他们有什么共同的特征呢? (4)小明发现,上面的三个图形都是轴对称图形,而且将它们分成全等的两部分的直线都有两条以上。因此,他认为,对于平面的任何轴对称图形,都存在两条以上的直线,可以将这个轴对称图形分成全等的两个部分。你认为他的观点正确吗?说说你的理由。 考查内容:通过观察、实验、猜想、证明等数学活动过程,作出合情推理和演译推理, (责任编辑:admin) |
