转换视角,轻松学函数
甘肃省会宁县枝阳中学 禄文夫
2011年中考试题中,对于求二次函数的解析式和二次函数的图像与坐标轴围成的三角形面积问题时,我们可以从不同的角度去考虑同一问题时,一般要熟悉二次函数的形式:⑴一般式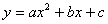 ;⑵交点式 ;⑵交点式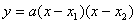 ,其中( ,其中(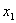 ,0),( ,0),(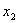 ,0)为抛物线与 ,0)为抛物线与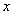 轴的交点坐标,并要理解其中的含义;⑵顶点式 轴的交点坐标,并要理解其中的含义;⑵顶点式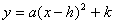 其中对称轴是 其中对称轴是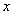 = =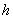 。解决这部分问题时,往往涉及一元二次方程根与系数关系相关计算;求直角三角形算面积时,往往与直角三角形相似问题相关或勾股定理的应用有直接的关系。因此,在平常学习二次函数的问题时,要善于从不同的角度思考,选择合理形式,寻找最佳的方法,与其它知识综合应用,以达到快速解题,使二次函数的一些问题便可迎刃而解。下面我们就以2011年广东肇庆第25题为例进行剖析. 。解决这部分问题时,往往涉及一元二次方程根与系数关系相关计算;求直角三角形算面积时,往往与直角三角形相似问题相关或勾股定理的应用有直接的关系。因此,在平常学习二次函数的问题时,要善于从不同的角度思考,选择合理形式,寻找最佳的方法,与其它知识综合应用,以达到快速解题,使二次函数的一些问题便可迎刃而解。下面我们就以2011年广东肇庆第25题为例进行剖析.
例(2011年广东肇庆)已知抛物线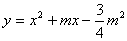 ( (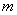 >0)与 >0)与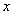 轴交于 轴交于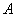 、 、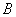 两点. 两点.
(1)求证:抛物线的对称轴在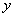 轴的左侧; 轴的左侧;
(2)若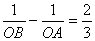 ( ( 是坐标原点),求抛物线的解析式; 是坐标原点),求抛物线的解析式;
(3)设抛物线与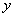 轴交于点 轴交于点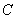 ,若D ,若D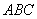 是直角三角形,求D 是直角三角形,求D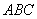 的面积. 的面积.
第一、二问:求证:抛物线的对称轴在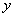 轴的左侧; 轴的左侧;
视角1(从对称轴的角度看)若二次函数的解析式是: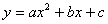 , 则二次函数的对称轴为: , 则二次函数的对称轴为: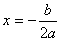 ,在解题时我们直接根据二次函数 ,在解题时我们直接根据二次函数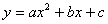 的对称轴 的对称轴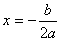 ,带入已知的相关信息便可求解. ,带入已知的相关信息便可求解.
解法1
(1)证明:∵对称轴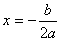 , ,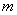 >0 ∴ >0 ∴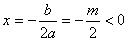 ∴抛物线的对称轴在 ∴抛物线的对称轴在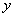 轴的左侧. 轴的左侧.
视角2(从与x轴交点的角度看)若二次函数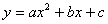 与x轴交点坐标为( 与x轴交点坐标为(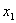 ,0),( ,0),(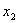 ,0),则 ,0),则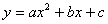 与x轴交点的横坐标实际上是一元二次方程 与x轴交点的横坐标实际上是一元二次方程 的两根 的两根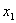 , ,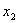 ,根据两根关系判断交点与原点的相对位置,一般利用一元二次方程根与系数的关系: ,根据两根关系判断交点与原点的相对位置,一般利用一元二次方程根与系数的关系: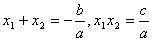 便可求解. 便可求解.
解法2(1)证明:设抛物线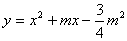 ( (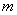 >0)与 >0)与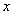 轴交点坐标为A( 轴交点坐标为A(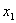 ,0),B( ,0),B(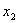 ,0),则 ,0),则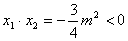 , ∴ , ∴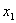 与 与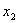 异号,由于 异号,由于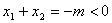 ,所以 ,所以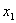 与 与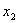 中绝对值大的一个为负数,∴抛物线的对称轴在 中绝对值大的一个为负数,∴抛物线的对称轴在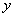 轴的左侧. 轴的左侧.
(2)设抛物线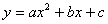 与 与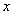 轴交点坐标为A( 轴交点坐标为A(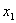 ,0),B( ,0),B(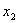 ,0),由于若 ,0),由于若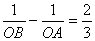 ,由于 ,由于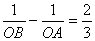 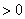 ∴ ∴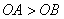 由(1)知:抛物线的对称轴在 由(1)知:抛物线的对称轴在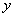 轴的左侧∴ 轴的左侧∴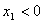 , ,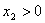 ∴ ∴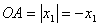 , ,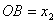 ∴由 ∴由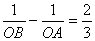 得: 得: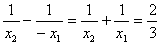 ,即 ,即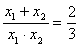 ,从而 ,从而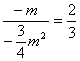 ,解得: ,解得: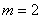
∴抛物线的解析式是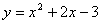
视角3(从顶点坐标的角度看)一般式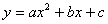 总可以化成 总可以化成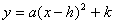 的形式,其中( 的形式,其中( )对称轴是 )对称轴是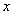 = =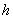 ,所以我们可以将二次函数的一般式转化成顶点式求解. ,所以我们可以将二次函数的一般式转化成顶点式求解.
解法3(1)∵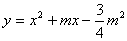 ( (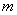 >0) >0)
∴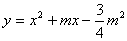 = =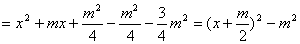
∴对称轴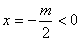 ∴抛物线的对称轴在 ∴抛物线的对称轴在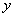 轴的左侧. 轴的左侧.
第三问:设抛物线与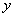 轴交于点 轴交于点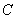 ,若D ,若D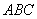 是直角三角形,求D 是直角三角形,求D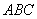 的面积. 的面积.
视角1(从三角形相似的角度看)直角三角形斜边上的高将直角三角形分成两个相似的直角三角形且与原直角三角形相似,由对应关系可得:斜边上高是高分斜边的两条线断的比例中项,依此代入相关信息便可求解。
解法1 如图: 当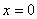 时, 时,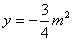
 
∴抛物线与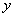 轴交点坐标为 轴交点坐标为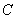 (0, (0, ) )
∵D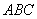 是直角三角形,且只能有AC⊥BC,又OC⊥AB, 是直角三角形,且只能有AC⊥BC,又OC⊥AB,
可得:Rt△AOC∽Rt△COB,
∴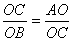 ,即 ,即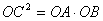 ∴ 即 ∴ 即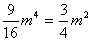 解得: 解得: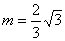 ∴ ∴ = =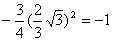 ,∴点 ,∴点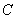 的坐标为(0,—1)∴OC=1 的坐标为(0,—1)∴OC=1
又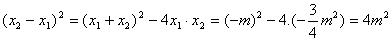
∵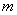 >0,∴ >0,∴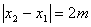 即AB= 即AB=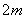
∴D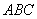 的面积= 的面积=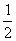 ×AB×OC= ×AB×OC=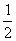 ? ?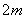 ?1= ?1=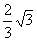
视角2(从勾股定理的角度看)直角三角形三边关系: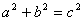 ,在解题过程中,我们找直角三角形三边的相关信息,应用勾股定理,代入已知信息便可转化成代数关系从而达到求解的目的. ,在解题过程中,我们找直角三角形三边的相关信息,应用勾股定理,代入已知信息便可转化成代数关系从而达到求解的目的.
解法2 如图:当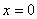 时, 时,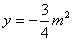 ∴点 ∴点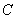 (0, (0, ) )
 
∵D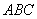 、D 、D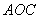 、D 、D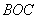 都是直角三角形 都是直角三角形
∴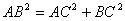
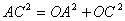 , ,
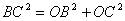
∴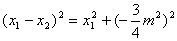 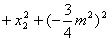
∴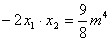 ∴ ∴ 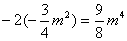
解得: 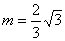
∴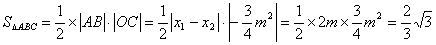
视角3(从三角函数的角度看)相同的角(或相等的角)的同一三角函数值相同,在直角三角形出现,特别是直角三角形斜边上的高为已知条件时,我们可以选择应用某同角或等角的同一三角函数来解决问题.
解法3 如图:当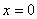 时, 时,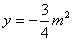
 
∴抛物线与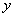 轴交点坐标为 轴交点坐标为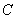 (0, (0, ) )
∵D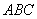 是直角三角形, 是直角三角形,
且只能有AC⊥BC,又OC⊥AB,
可得: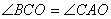 ∴Rt△AOC∽Rt△COB, ∴Rt△AOC∽Rt△COB,
∴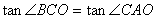 ∵ ∵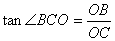 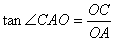
∴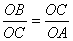 ,即 ,即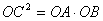 ∴ ∴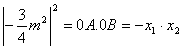
即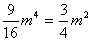 解得: 解得: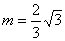 ∴ ∴ = =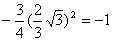
∴点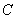 的坐标为(0,—1)∴OC=1 的坐标为(0,—1)∴OC=1
又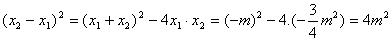
∵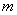 >0,∴ >0,∴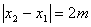 即AB= 即AB=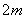
∴D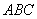 的面积= 的面积=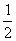 ×AB×OC= ×AB×OC=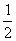 ? ?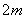 ?1= ?1=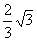
视角4(从面积的角度看)同一图形的面积是确定的,我们可以从不同的角度计算同一图形的面积,与勾股定理结合,使其系转化成代数关系达到求解的目的.
解法4 如图:当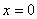 时, 时,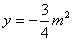 ∴点 ∴点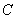 (0, (0, ) )
 
∵D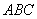 、D 、D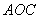 、D 、D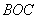 都是直角三角形 都是直角三角形
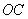 是 是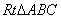 D D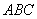 斜边上的高 斜边上的高
∴
∵ 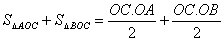
∴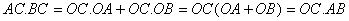
∴
∵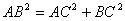 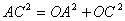 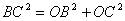
∴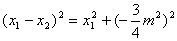 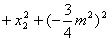
∴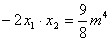 ∴ ∴ 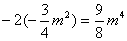 解得: 解得: 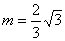
∴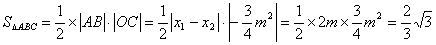 .
(责任编辑:admin) .
(责任编辑:admin) |
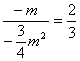 ,解得:
,解得:







