|
☆☆☆ 点击下载试题 ☆☆☆  各位同学在查看时请点击全屏查看 各位同学在查看时请点击全屏查看2018年晋城中考数学模拟试题 注意事项: 1.本试卷分为第I卷和第II卷两部分,考试时间为120分钟。 2.答选择题前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束后,试题和答题卡一并收回,每题选出答案后,必须用2B铅笔把答题卡上对应的答案标号【ABCD】涂黑,如需改动,先用橡皮擦干净,再改涂其他答案,答在试题卷上无效。 第I卷选择题(共20分) 一.数学模拟试题选择题(在每小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡将该项涂黑,本大题共10个小题,每小题2分,共20分) 1.下列各式正确的是() A. 2. 下面的图形中,是中心对称图形的是( )  3.用配方法解方程 A. C. 4.已知 A.1 B.3 C.-3 D.-1 5.为迎接北京奥运会,有十五位同学参加奥运知识竞赛,且他们的分数互不相同,取八位同学进入决赛,某人知道了自己的分数后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛 ( ) A.平均数 B.众数 C.最高分数 D.中位数 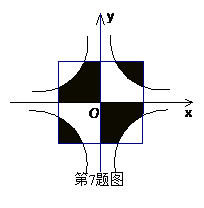 6.只用下列图形不能镶嵌的是( ) 6.只用下列图形不能镶嵌的是( )A.正三角形 B.四边形 C.正五边形 D.正六边形 7.如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴, 反比例函数 A.2 B.4 C.8 D.6 8.如图,一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是( ) A. 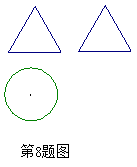 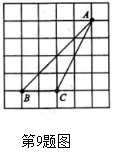 9.在正方形网格中,△ABC的位置如图所示,则tan∠A的值为() A. 10.抛物线 A.向左平移1个单位,再向下平移3个单位 B.向左平移1个单位,再向上平移3个单位 C.向右平移1个单位,再向下平移3个单位 D.向右平移1个单位,再向上平移3个单位 第II卷非选择题(共100分)
二.填空题(本大题共8小题,每小题3分,共24分.把答案填在题中横线上) 11. 12.当x=___________时,分式 13.在数轴上与表示 14.据市统计局初步核算,去年我市实现地区生产总值1583.45亿元.这个数据用科学记数法表示约为元(保留三位有效数字). 15.某篮球运动员投3分球的命中率为0.5,投2分球的命中率为0.8,一场比赛中据说他投了20次2分球, 投了6次3分球,估计他在这场比赛中得了 ______ 分. 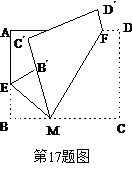 16.如图所示,某河堤的横断面是梯形 16.如图所示,某河堤的横断面是梯形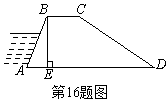 17.如图,把一张长方形的纸片按如图所示的方式折叠,EM、FM为折痕,折叠后的C点落在 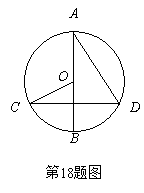 18.已知:AB是⊙O的直径,弦CD⊥AB,连结OC、AD, 18.已知:AB是⊙O的直径,弦CD⊥AB,连结OC、AD,∠OCD=32°,则∠A=_____.  三.解答题:(本大题共8小题,共76分.解答应写出必要的文字说明.证明过程或演算步骤.) 三.解答题:(本大题共8小题,共76分.解答应写出必要的文字说明.证明过程或演算步骤.) 19.解不等式(6分) 示出它的解集。
20.解方程(6分)
 21.(本题8分) 如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段EF与图中哪一条线段相等?先将你的猜想出的结论填写在下面的横线上,然后再加以证明. 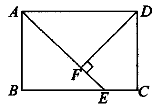 即EF=________. 即EF=________.
22.(本题9分)  如图,A,B,C,D四张卡片上分别写有 如图,A,B,C,D四张卡片上分别写有(1)从中任取一张卡片,求取到的数是无理数的概率. (2)从中任取两张卡片,求取到的两个数的和是无理数的概率.(利用树状图或列表法)
23.(本题9分) 在盘点北京2008年奥运会成绩单时,有这样的信息:第一次获得奥运奖牌的国家,多哥:布克佩蒂 皮划艇激流回旋 铜牌;塔吉克斯坦:拉苏尔·博基耶夫 柔道 铜牌;阿富汗:尼帕伊 跆拳道 铜牌;毛里求斯:布鲁诺·朱利 拳击 铜牌; 苏丹:艾哈迈德 男子800米 银牌。(1)请用一张统计表简洁地表示上述信息; (2)你从这些信息中发现了什么?
24.(本题12分)  如图,在△ABC中,AC=2,BC=3,AB=4.D是BC边上一点,直线DE∥AC交BC于D,交AB于E,CF∥AB交直线DE于F. 如图,在△ABC中,AC=2,BC=3,AB=4.D是BC边上一点,直线DE∥AC交BC于D,交AB于E,CF∥AB交直线DE于F. (1)求证:△CFD∽△BAC. (2)设CD=x,ED=y,求y与x的函数关系式. (3)若四边形EACF是菱形,求出DE的长.
25.(本题12分) 2008年以来随着金融危机的不断曼延,我市某县的返乡农民工逐渐增多,政府部门决定利用现有经过培训的349名男职工和295名女职工推荐到某企业生产A、B两种大型产品共50个。已知生产一个 请你根据所学知识为这家企业分析A、B两种大型产品如何调配,问符合题意的调配方案有几种?请你帮助设计出来;如果为了扩大就业,企业应选择哪种方案? 
26.(本题14分) 已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D.E,连结AD、BD、BE。 (1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形。 _____________________,______________________ 。 (2)直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系(如图2),若抛物线y=ax2-2ax-3a(a<0)经过点A.B.D,且B为抛物线的顶点。 ①写出顶点B的坐标(用a的代数式表示)___________。 ②求抛物线的解析式。 ③在x轴下方的抛物线上是否存在这样的点P:过点P做PN⊥x轴于N,使得△PAN与△OAD相似?若存在,求出点P的坐标;若不存在,说明理由。 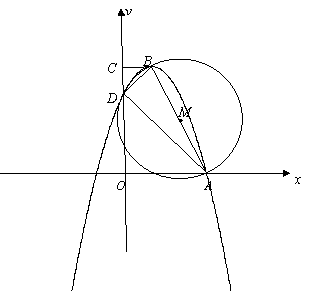 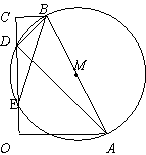 2018年晋城中考数学模拟试题参考答案 一.1~5.CDBAD 6~10.CCDCA 7.将 8.由题可知,这个几何体是底面直径为1.母线为1的圆锥体。它的侧面积= 9.由题意,∠B=45°,过C点作AB的垂线必过小正方形网格顶点, 可知tan∠A= 二.11. 三.19.解:移项得  数轴略。……6分 20.解:去分母,  检验:把x=2代入最简分母中6x-2≠0,x=2是方程的解 所以原方程的解为x=2.……6分 21.EF=EC,………2分 证明:在矩形ABCD中,AD=BC,AD∥BC……3分 在△ADE中,∠AFD=∠B,∠DAF=∠AEB ,AD=AE,………5分 ∴△ADF≌△EAB.……………6分 ∴AF=BE…………………………7分 又∵AE=AD=BC,∴EF=EC…………8分 22.(1)四张卡片中只有BD两张是无理数,所以P(无理数)= (2)列表:
……………6分 其中和为无理数的是(AB)(AD)(BA)(DA)(BC)(CD)(CB)(DC) 所以,P (和为无理数)= 23.(1)
……………6分 (2)奥运奖牌不是大国的专利,奥运精神已深入到世界各国人民心中,各国运动员的竞技水平不断提高。………9分 24.解:(1)∵EF∥AC,∴∠FDC=∠BCA……2分 ∵AE∥CF,∴∠FCD=∠B ∴△CFD∽△BAC.………4分 (2)∵EF∥AC,AE∥CF,∴四边形ACFE是平行四边形. ∴EF=AC…………5分 ∵△CFD∽△BAC,∴ ∴y=2- (3)四边形ACFE是菱形,∴CF=AC=2.……………9分 ∵△CFD~△BAC,∴ ∴DE=1…………………12分 25.解:设生产 依题意,得: 解这个不等式组,得: ① ② ③ 其中①需职工343+295=638人 ②需职工346+290=636人 ③需职工349+285=643人, 所以,如果为了扩大就业,企业应选择方案③。………12分 26.(1)△OAD∽△CDB. △ADB∽△ECB………4分 (2)①(1,-4a)……………5分 ②∵△OAD∽△CDB ∴ ∵ax2-2ax-3a=0,可得A(3,0)……………8分 又OC=-4a,OD=-3a,CD=-a,CB=1, ∴ 故抛物线的解析式为: ③存在,…………11分 设P(x,-x2+2x+3) ∵△PAN与△OAD相似,且△OAD为等腰三角形 ∴PN=AN 当x<0(x<-1)时,-x+3=-(-x2+2x+3),x1=-2,x2=3(舍去), ∴P(-2,-5)…13分 当x>0(x>3)时,x-3= -(-x2+2x+3), x1=0,x2=3(都不合题意舍去) 符合条件的点P为(-2,-5)…………14分 (责任编辑:admin) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
