|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看 2018年昆明中考数学冲刺试题 (全卷共三个大题,共23个小题,共4页;满分120分,考试时间120分钟) 一、数学冲刺试题填空题(本大题共6小题,每小题3分,共18分) 1.2017年我国约有9 400 000人参加高考,将9 400 000用科学记数法表示为__9.4×106__. 2.若代数式有意义,则x的取值范围是__x≥1__. 3.一个n边形的内角和是720°,则n=__6__. 4.如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM=__30__°. 5.如图,直线y=x+4与双曲线y=(k≠0)相交于A(-1,a),B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为____. 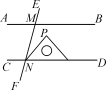 (第4题图) (第4题图)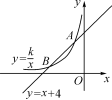 (第5题图) (第5题图)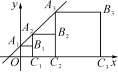 (第6题图) (第6题图)6.正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1,A2,A3…在直线y=x+1上,点C1,C2,C3…在x轴上,则An的坐标是__(2n-1-1,2n-1)__. 二、填空题(本大题共8小题,每小题只有一个正确答案,每小题4分,共32分) 7.-|-2|的倒数是( C ) A.2 B. C.- D.-2 8.下列运算正确的是( D ) A.(-2a3)2=-4a6 B.=±3 C.m2·m3=m6 D.x3+2x3=3x3 9.下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( C ) A B C D 10.某校九年级(1)班全体学生2017年初中毕业体育考试的成绩统计如表:
根据表中的信息判断,下列结论中错误的是( D ) A.该班一共有40名同学 B.该班学生这次考试成绩的众数是45分 C.该班学生这次考试成绩的中位数是45分 D.该班学生这次考试成绩的平均数是45分 11.已知点M(1-2m,m-1)在第四象限,则m的取值范围在数轴上表示正确的是( B ) A B C D 12.点A(a,4),点B(3,b)关于x轴对称,则(a+b)2 017的值为( B ) A.0 B.-1 C.1 D.72 017 13.如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2 m,另一边减少了3 m,剩余一块面积为20 m2的矩形空地,则原正方形空地的边长是( A ) A.7 m B.8 m C.9 m D.10 m 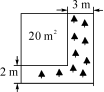 (第13题图) (第13题图)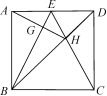 (第14题图) (第14题图)14.如图,正方形ABCD中,点E是AD边中点,BD,CE交于点H,BE,AH交于点G,则下列结论:①AG⊥BE;②BG=4GE;③S△BHE=S△CHD;④∠AHB=∠EHD. 其中正确的个数是( D ) A.1 B.2 C.3 D.4 三、解答题(本大题共9小题,共70分) 15.(5分)先化简,再求值:÷,其中x=-1. 解:原式=÷ =÷ =× =, 把x=-1代入,原式====. 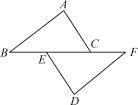 16.(6分)如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D. (1)求证:AC∥DE; (2)若BF=13,EC=5,求BC的长. 解:(1)在△ABC和△DFE中, ∴△ABC≌△DFE(SAS), ∴∠ACE=∠DEF, ∴AC∥DE; (2)∵△ABC≌△DFE, ∴BC=EF, ∴CB-EC=EF-EC, ∴EB=CF. ∵BF=13,EC=5, ∴EB==4, ∴CB=4+5=9. 17.(5分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(1,2),B(3,1)(每个方格的边长均为1个单位长度). (1)将△OAB向右平移1个单位长度后得到△O1A1B1,请画出△O1A1B1; (2)请以O为位似中心画出△O1A1B1的位似图形,使它与△O1A1B1的相似比为2∶1; (3)点P(a,b)为△OAB内一点,请直接写出位似变换后的对应点P′的坐标为________. 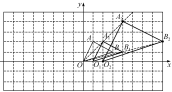 解:(1)如图,△O1A1B1即为所求作三角形; (2)如图,△O2A2B2即为所求作三角形; (3)(2a+2,2b). 18.(8分)某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: (1)这次被调查的学生共有________人; (2)请你将条形统计图补充完整; (3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率.(用树状图或列表法解答) 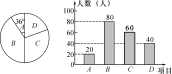 图① 图② 解:(1)200; (2)C项目对应人数为:200-20-80-40=60(人);补图如图; (3)列表如下:
∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种, ∴P(选中甲、乙)==. 19.(7分)如图,已知点E,F分别是▱ABCD的边BC,AD上的中点,且∠BAC=90°. 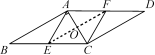 (1)求证:四边形AECF是菱形; (2)若∠B=30°,BC=10,求菱形AECF面积. 解:(1)∵四边形ABCD是平行四边形, ∴AD=BC. ∵E,F分别是BC,AD的中点,∴AF=AD=BC=EC. 在Rt△ABC中,∠BAC=90°,点E是BC边的中点, ∴AE=BC=CE, 同理,AF=AD=CF, ∴AE=CE=AF=CF, ∴四边形AECF是菱形; (2)连接EF交AC于点O. 在Rt△ABC中,∠BAC=90°,∠B=30°,BC=10, ∴AC=BC=5,AB=AC=5. ∵四边形AECF是菱形, ∴AC⊥EF,OA=OC, ∴OE是△ABC的中位线, ∴OE=AB=,∴EF=5, ∴S菱形AECF=AC·EF=×5×5=. 20.(7分)钟楼是云南大学的标志性建筑之一,某校数学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7 m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数)  解:∵在Rt△ACD中,∠ACD=∠CAD=45°, ∴AD=CD,设AD=CD=x m, ∵AD=AB+BD, ∴BD=AD-AB=(x-7)m. ∵在Rt△BCD中,∠BCD=90°-∠CBD=36°, tan∠BCD=, ∴tan36°=,∴x·tan36°=x-7, ∴x≈26.即CD≈26 m. 答:钟楼的高度CD约为26 m. 21.(10分)某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元. (1)求购进甲、乙两种花卉,每盆各需多少元; (2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式; (3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元? 解:(1)设购进甲种花卉每盆m元,乙种花卉每盆n元. 由题意得解得 即购进甲种花卉每盆16元,乙种花卉每盆8元; (2)由题意可得,W=6x+×1=4x+100, 即W与x之间的函数关系式是:W=4x+100; (3)由题意得解得10≤x≤12.5,且x为整数, 故有三种购买方案, 方案一:购进甲种花卉10盆,乙种花卉80盆; 方案二:购进甲种花卉11盆,乙种花卉78盆; 方案三:购进甲种花卉12盆,乙种花卉76盆. 由W=4x+100可知,W随x的增大而增大, 故方案三获利最大,此时W=4×12+100=148(元), 即最大利润是148元. 22.(10分)如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 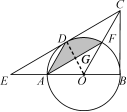 (1)求证:CB是⊙O的切线; (2)若∠ECB=60°,AB=6,求图中阴影部分的面积. 解:(1)连接OD,与AF相交于点G. ∵CE与⊙O相切于点D, ∴OD⊥CE, ∴∠CDO=90°. ∵AD∥OC, ∴∠ADO=∠DOC,∠DAO=∠BOC. ∵OA=OD,∴∠ADO=∠DAO, ∴∠DOC=∠BOC. 在△CDO和△CBO中, ∴△CDO≌△CBO, ∴∠CBO=∠CDO=90°,∴CB是⊙O的切线; (2)由(1)可知∠DCO=∠BCO,∠DOC=∠BOC, ∵∠ECB=60°, ∴∠DCO=∠BCO=∠ECB=30°, ∴∠DOC=∠BOC=60°, ∴∠DOA=60°. ∵OA=OD, ∴△OAD是等边三角形, ∴AD=OD=OF. ∵∠GOF=∠ADO, 在△ADG和△FOG中, ∴△ADG≌△FOG,∴S△ADG=S△FOG. ∵AB=6,∴⊙O的半径r=3, ∴S阴=S扇形ODF==π. 23.(12分)如图,在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC. (1)直接写出点A的坐标,并求直线l的函数解析式;(其中k,b用含a的式子表示) (2)点E是直线l上方的抛物线上一点,若△ACE的面积的最大值为,求a的值; (3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由. 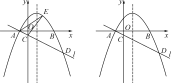 (备用图) 解:(1)A(-1,0). 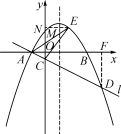 图① 如图①,作DF⊥x轴于F, ∴DF∥OC,∴=, ∵CD=4AC,∴==4. ∵OA=1,∴OF=4, ∴D点的横坐标为4, 代入y=ax2-2ax-3a,得y=5a, ∴D(4,5a), 把A,D坐标代入y=kx+b得 解得 ∴直线l的函数解析式为y=ax+a. (2)如图①,过点E作EN⊥y轴于点N.AE与y轴交于点M, 设点E[m,a(m+1)(m-3)],yAE=k1x+b1, 则 解得 ∴yAE=a(m-3)x+a(m-3),M[0,a(m-3)]. ∵MC=yM-yC=a(m-3)-a,NE=m, ∴S△ACE=S△ACM+S△CEM=·MC·|xA|+·MC·|xE|=MC·(xE-xC)=(m+1)[a(m-3)-a]=-a, ∴有最大值-a=,∴a=-; (3)令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0, 解得:x1=-1(舍去),x2=4,∴D(4,5a). ∵y=ax2-2ax-3a=a(x-1)2-4a, ∴抛物线的对称轴为直线x=1, 设P(1,m). 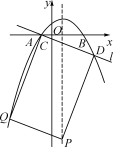 图② ①如图②,若AD是矩形的一条边, 由AQ∥DP知xD-xP=xA-xQ, 即4-1=-1-xQ,∴xQ=-4. 将x=-4代入抛物线方程得Q(-4,21a), m=yD+yQ=21a+5a=26a,则P(1,26a). ∵四边形ADPQ为矩形,∴∠ADP=90°, ∴AD2+PD2=AP2, ∴[4-(-1)]2+(5a)2+(1-4)2+(26a-5a)2=(-1-1)2+(26a)2, 即a2=,∵a<0,∴a=-, ∴P1; 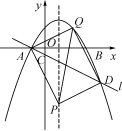 图③ ②如图③,若AD是矩形的一条对角线, (xA+xD)=(xQ+xP), ∴xQ=2,将xQ=2代入抛物线解析式得yQ=-3a,故Q(2,-3a), m=5a-(-3a)=8a,则P2(1,8a). ∵四边形ADPQ为矩形,∴∠APD=90°, ∴AP2+PD2=AD2. ∵AP2=[1-(-1)]2+(8a)2=22+(8a)2, PD2=(4-1)2+(5a-8a)2=32+(3a)2, AD2=[4-(-1)]2+(5a)2=52+(5a)2, ∴22+(8a)2+32+(3a)2=52+(5a)2, 解得a2=,∵a<0,∴a=-, ∴P2(1,-4). 综上可得,以点A,D,P,Q为顶点的四边形能成为矩形,P点的坐标为(1,-4)或. 第1页 (责任编辑:admin) |
