|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况,在查看时请点击右上角全屏查看 2017年永州市中考数学试题 一、选择题(每小题4分,共10小题,合计40分) 1.-8的绝对值是( ) A.8 B.-8 C. 2.x=1是关于x的方程2x-a=0的解,则a的值是( ) A.-2 B.2 C.-1 D.1 3.江永女书诞生于宋朝,是世界上唯一一种女性文字,主要书写在精制布面、扇面、布帕等物品上,是一种独特而神奇的文化现象.下列四个文字依次为某女书传人书写的“女书文化”四个字,基本是轴对称图形的是( )  4.下列运算正确的是( ) A.a·a2=a2 B.(ab)2=ab C. 5.下面是某一天永州市11个旅游景区最高气温(单位:℃)的统计表:
则下列说法正确的是( ) A.该组数据的方差为0 B.该组数据的平均数为25 C.该组数据的中位数为27 D.该组数据的众数为28 6.湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉  7.小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( ) A.AB,AC边上的中线的交点 B.AB,AC边  8.如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( ) A.1 B.2 C.3 D.4  9.在同一平面直角坐标系中,函数y=x+k与y=  10.已知从n个人中,选出m个人按照一定的顺序排成一行,所有不同的站位方法有n×(n-1)×…×(n-m+1)种.现某校九年级甲、乙、丙、丁4名同学和1位老师共5人在毕业前合影留念(站成一行),若老师站在中间,则不同的站位方法有( ) A.6种 B.20种 C.24种 D.120种 二、填空题:(每小题4分,共8小题,合计32分) 11.2017年端午小长假的第一天,永州市共接待旅客约275 000人次,请将275 000用科学记数法表示为___________________. 12.满足不等式组 13.某水果店搞促销活动,对某种水果打8折出售,若用60元钱买这种水果,可以比打折前多买3斤.设该种水果打折前的单价为x元,根据题意可列方程为_________ 14.把分别写有数字1,2,3,4,5的5张同样的小卡片放进不透明的盒子里,搅拌均匀后随机取出一张小卡片,则取出的卡片上的数字大于3的概率是________________. 15.(2017湖南永州)如图,已知反比例函数y=  16.如图,四边形ABCD是⊙O的内接四边形,点D是的中点,点E是上的一点,若∠CED=40°,则∠ADC=________度.  17.如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是_____________cm2(结果保留  18.一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下. (1)小球第3次着地时,经过的总路程为________________m; (2)小球第n次着地时,经过的总路程为________________m.  三、解答题:本大题共8个小题,满分78分. 19.(本小题满分8分)计算: 20.(本小题满分8分)先化简,再求值: 21.(本小题满分8分)某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图. 请结合图中的信息解答下列问题: (1)本次调查的人数为___________,其中防校园欺凌意识薄弱的人数占_________%; (2)补全条形统计图; (3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数; (4)请你根据题中的信息,给该校的安全教育提一个合理的建议. 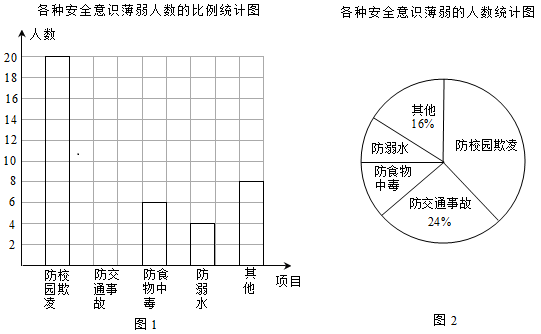 22.(本小题满分10分)如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E. (1)求证:AF=CE; (2)若DE=2, 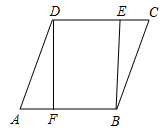 23.(本小题满分10分)永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
(1)请建立该水库水位y与日期x之间的函数模型; (2)请用求出的函数表达式预测该水库今年4月6日的水位; (3)你能用求出的函数表达式预测该水库今年12月1日的水位吗? 24.(本小题满分10分)如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC. (1)求证:PC是⊙O的切线; (2)若∠P=60°,PC=2,求PE的长. 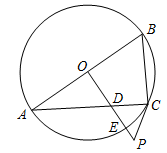 25.(本小题满分12分)如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点. (1)求该抛物线的解析式; (2)阅读理解: 在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数,且k1≠0),直线l2:y=k2x+b2(k2,b2为常数,且k2≠0),若l1⊥l2,则k1·k2=-1. 解决问题: ①若直线y=3x-1与直线y=mx+2互相垂直,求m的值; ②是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由; (3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值. 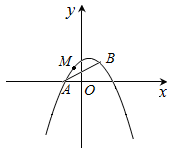 26.(本小题满分12分)已知点O是正方形ABCD对角线BD的中点. (1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N. ①∠AEM=∠FEM; ②点F是AB的中点; (2)如图2,若点E是OD上一点,点F是AB上一点,且使 (3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 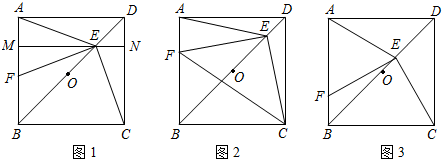 2017年湖南省永州市中考数学试卷(解析版) 一、选择题(每小题4分,共10小题,合计40分) 1.-8的绝对值是( ) A. 答案:A. 解析:负数的绝对值是它的相反数,所以-8的绝对值是8. 2.x=1是关于x的方程2x-a=0的解,则a的值是( ) A.-2 B.2 C.-1 D.1 答案:B, 解析:把x=1代入方程2x-a=0得2-a=0,解得a=2. 3.江永女书诞生于宋朝,是世界上唯一一种女性文字,主要书写在精制布面、扇面、布帕等物品上,是一种独特而神奇的文化现象.下列四个文字依次为某女书传人书写的“女书文化”四个字,基本是轴对称图形的是( )  答案:A, 解析:选项A是轴对称图形,选项B、C、D都不是轴对称图形,判断一个图形是不是轴对称图形,关键在于看是否存在一条直线,使得这个图形关于这条直线对称. 4.下列运算正确的是( ) A.a·a2=a2 B.(ab)2=ab C. 答案:C, 解析:选项A属于同底数幂相乘,底数不变,指数相加,所以a·a2=a3,选项A错误;选项B属于积的乘方,等于把积的各个因式分别乘方,所以(ab)2=a2b2,选项B错误;选项C考查负整数指数幂,根据 5.下面是某一天永州市11个旅游景区最高气温(单位:℃)的统计表:
则下列说法正确的是( ) A.该组数据的方差为0 B.该组数据的平均数为25 C.该组数据的中位数为27 D.该组数据的众数为28 答案:D, 解析:这组数据的平均数是 6.湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”的主视图,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )  答案:D, 解析:物体的主视图是由正面看到的图形,应选D. 7.小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( ) A.AB,AC边上的中线的交点 B.AB,AC边上的垂直平分线的交点 C.AB,AC边上的高所在直线的交点 D.∠BAC与∠ABC的角平分线的交点  [来源:学§科§网Z§X§X§K][来源:Zxxk.Com] [来源:学§科§网Z§X§X§K][来源:Zxxk.Com]答案:B, 解析:本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,故选B. 8.如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( ) A.1 B.2 C.3 D.4  答案:C, 解析:∵∠ACD=∠B,∠A=∠A,∴△ACD∽△ABC,∴ 9.在同一平面直角坐标系中,函数y=x+k与y=  答案:B, 解析:选项A中,由一次函数y=x+k的图象知k<0,由反比例函数y= 10.已知从n个人中,选出m个人按照一定的顺序排成一行,所有不同的站位方法有n×(n-1)×…×(n-m+1)种.现某校九年级甲、乙、丙、丁4名同学和1位老师共5人在毕业前合影留念(站成一行),若老师站在中间,则不同的站位方法有( ) A.6种 B.20种 C.24种 D.120种 答案:D, 解析:5个人中选出4个 二、填空题:(每小题4分,共8小题,合计32分) 11.2017年端午小长假的第一天,永州市共接待旅客约275 000人次,请将275 000用科学记数法表示为___________________. 答案:2.75×105, 解析:275 000=2.75×105. 12.满足不等式组 答案:0, 解析:解不等式①得x≤ 13.某水果店搞促销活动,对某种水果打8折出售,若用60元钱买这种水果,可以比打折前多买3斤.设该种水果打折前的单价为x元,根据题意可列方程为________________. 答案: 解析:本题的等量关系是:打折后买的水果数=打折前买的水果数+3,打折后买的水果数为 14.把分别写有数字1,2,3,4,5的5张同样的小卡片放进不透明的盒子里,搅拌均匀后随机取出一张小卡片,则取出的卡片上的数字大于3的概率是________________. 答案: 解析:大于3的有2张,卡片总数为5张,根据概率公式可得相应概率为 15.(2017湖南永州)如图,已知反比例函数y=  答案:-2, 解析:设点A的坐标为(m,n),因为点A在y= 16.如图,四边形ABCD是⊙O的内接四边形,点D是的中点,点E是上的一点,若∠CED=40°,则∠ADC=________度.  答案:100, 解析:连接AE,∵点D是的中点,∴∠AED=∠CED=40°,∴∠AEC=80°.∵∠AEC+∠ADC=180°,∴∠ADC=180°-∠AEC=180°-80°=100°. 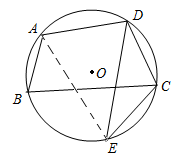 17.如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是_____________cm2(结果保留  答案: 解析:PB= 18.一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下. (1)小球第3次着地时,经过的总路程为________________m; (2)小球第n次着地时,经过的总路程为________________m.  答案:(1) 解析:小球第1次着地时,经过的总路程为1m;小球第2次着地时,经过的总路程为1+ 三、解答题:本大题共8个小题,满分78分. 19.(本小题满分8分)计算: 思路分析:根据特殊角的三角函数值、零指数幂、二次根式等各个知识点分别进行计算,然后根据实数的运算法则求得计算结果., 解:原式= 20.(本小题满分8分)先化简,再求值: 思路分析:先通分,同时把除法转化为乘法,再约分,化为最简分式;选择合适的数代入求值时,要注意使得分式的分母不能等于0,包括在分式化简过程中的分母都不能等于0. 解:原式= x不能取0,2,只能取x=1,原式= 21.(本小题满分8分)某校组织了一次防溺水、防交通事故、防食 请结合图中的信息解答下列问题: (1)本次调查的人数为___________,其中防校园欺凌意识薄弱的人数占_________%; (2)补全条形统计图; (3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数; (4)请你根据题中的信息,给该校的安全教育提一个合理的建议.  思路分析:(1)用“其他”的人数除以“其他”所占的百分比可得总人数,防校园欺凌意识薄弱的人数除以总人数即可该项目所占的百分比;(2)防交通事故的百分比乘总人数得到该项目的人数,再画图;(3)用样本估计总体,防溺水意识薄弱的人数的百分比乘总人数可得到总体中该项目的人数;(4)答案不唯一,合理即可. 解:(1)本次调查的人数为8÷16%=50,其中防校园欺凌意识薄弱的人数占20÷50×100%=40%,所以答案为50, 40; (2)防交通事故意识薄弱的人数为24%×50=12,补全图形如图; 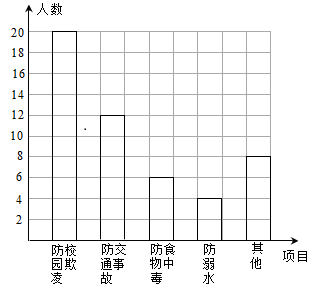 (3)1500× (4)答案不唯一,合理即可,如:应加强防校园欺凌的宣传力度,培养同学们的安全意识. 22.(本小题满分10分)如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E. (1)求证:AF=CE; (2)若DE=2,BE=4,求sin∠DAF的值.  思路分析:(1)根据AAS证明△ADF≌△CBE;(2)设BC=x,则CE=x-2,在Rt△BCE中,根据勾股定理得BE2+CE2=BC2列出关系x的方程,求出BC的长;在Rt△BCE中,可求得sin∠C的值,即为sin∠DAF的值. 解:(1)证明:∵四边形ABCD是菱形,∴AD=BC,∠A=∠C.又DF⊥AB,BE⊥CD,∴∠AFD=∠CEB=90°,在△ADF和△CBE中,∠AFD=∠CEB,∠A=∠C,AD=CB,∴△ADF≌△CBE.∴AF=CE. (2)解:设BC=x,则CE=x-2,在Rt△BCE中,BE2+CE2=BC2,∴42+(x-2)2=x2,∴x=5,∴sin∠DAF=sin∠C= 23.(本小题满分10分)永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
(1)请建立该水库水位y与日期x之间的函数模型; (2)请用求出的函数表达式预测该水库今年4月6日的水位; (3)你能用求出的函数表达式预测该水库今年12月1日的水位吗? 思路分析:(1)先判断是一次函数,再用待定系数法求得解析式;(2)把x=6代入(1)中求得的解析计算即可;(3)不能,因为用所建立的函数模型远离已知数据作预测是不可靠的. 解:(1)水库水位y随日期x的变化是均匀的,因此水库水位y与日期x之间是一次函数关系.设y=kx+b,把x=1,y=20.00和x=2,y=20.50代入得: (2)当x=6时,y=0.5×6+19.5=22.50. (3)不能,因为用所建立的函数模型远离已知数据作预测是不可靠的. 24.(本小题满分10分)如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC. (1)求证:PC是⊙O的切线; (2)若∠P=60°,PC=2,求PE的长.  思路分析:(1)连接OC,由OB=OC及已知可得∠PCA=∠OCB.由直径所对的圆周角为直角有∠ACB=90°,从而可得∠OCP=90°,所以PC是⊙O的切线;(2)在Rt△PCO中,利用∠P的正切和正弦分别求得OC、OP的长,再根据PE=OP-OE计算即可. 解:(1)连接OC. ∵OB=OC,∴∠ABC=∠OCB. 又∠PCA=∠ABC,∴∠PCA=∠OCB.∵AB为⊙O直径,∴∠ACB=90°. ∴∠ACO+∠OCB=90°,∴∠ACO+∠PCA=90°,即∠OCP=90°,∴PC是⊙O的切线; (2)在Rt△PCO中,tan∠P= 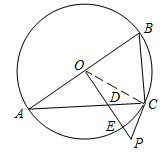 25.(本小题满分12分)如图,已知抛物线y=ax2+bx+1经过A(-1,0 (1)求该抛物线的解析式; (2)阅读理解: 在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数 解决问题: ①若直线y=3x-1与直线y=mx+2互相垂直,求m的值; ②是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由; (3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.  思路分析:(1)把A(-1,0),B(1,1)两点代入y=ax2+bx+1求解;(2)①根据k1·k2=-1计算;②先求出直线PA的表达式,从而可得与AB垂直的直线的k的值,然后分两种情况讨论:∠PAB=90°与∠PBA=90°,分别求出另一条直角边所在直线的表达式,与二次函数表达式联立方程组求解,得到点P的坐标;(3)△ABM的底边AB不变,当△ABM的面积取最大值时,点M到直线AB的距离有最大值,因此把问题转化为求△ABM的面积最大值问题,这样只要建立关于△ABM的面积的二次函数关系式,再化为顶点式即可. 解:(1)根据题意得: 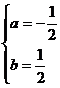 ∴y= ∴y=(2)①3m=-1,∴m= ②设PA的表达式为y=kx+c,过A(-1,0),B(1,1)两点的直线表达式为 若∠PAB=90°,把 A(-1,0)代入得0=-2×(-1)+c,解得c=-2,∴y=-2x-2,点P是直线PA与抛物线的交点,联立方程组: 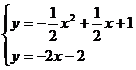 解得 解得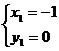 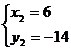 ∴P(6,-14); ∴P(6,-14);若∠PBA=90°,把B(1,1)代入y=-2x+c,得1=-2×1+c,解得c=3,∴y=-2x+3,点P是直线PB与抛物线的交点,联立方程组: 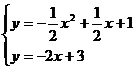 解得 解得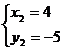 ∴P(4,-5). ∴P(4,-5).综上所述,存在点P(6,-14)或(4,-5),使得△PAB是以AB为直角边的直角三角形. (3)设M(n, ∴S△ABM= 26.(本小题满分12分)已知点O是正方形ABCD对角线BD的中点. (1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N. ①∠AEM=∠FEM; ②点F是AB的中点; (2)如图2,若点E是OD上一点,点F是AB上一点,且使 (3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当  思路分析:(1)①过点E作EG⊥BC,垂足为G,根据ASA证明△CEG≌△FEM得CE=FE,再根据SAS证明△ABE≌△CBE 得AE=CE,在△AEF中根据等腰三角形“三线合一”即可证明结论成立;②设AM=x,则AF=2x,在Rt△DEN中,∠EDN=45°,DE= 解:(1)①过点E作EG⊥BC,垂足为G,则四边形MBGE为正方形,ME=GE,∠MFG=90°,即∠MEF+∠FEG=90°,又∠CEG+∠FEG=90°,∴∠CEG=∠FEM.又GE=ME,∠EGC=∠EMF=90°,∴△CEG≌△FEM.∴CE=FE,∵四边形ABCD为正方形,∴AB=CB,∠ABE=∠CBE=45°,BE=BE,∴△ABE≌△CBE.∴AE=CE,又CE=FE,∴AE=FE,又EM⊥AB, ∴∠AEM=∠FEM. ②设AM=x (2)△EFC是等腰直角三角形.过点E作EM⊥AB,垂足为M,延长ME交CD于点N,过点E作EG⊥BC,垂足为G.则△AEM≌△CEG(HL),∴∠AEM=∠CEG,设AM=x,则DN=AM=x,DE = (3) 过点E作EM⊥AB,垂足为M,延长ME交CD于点N,过点E作EG⊥BC,垂足为G.则△AEM≌△CEG(HL),∴∠AEM=∠CEG. ∵EF⊥CE,∴∠FEC =90°,∴∠CEG+∠FEG=90°.又∠MEG =90°,∴∠MEF+∠FEG=90°,∴∠CEG=∠MEF,∵∠CEG =∠AEF,∴∠AEF=∠MEF,∴△AEM≌△FEM (ASA),∴AM=FM.设AM=x,则AF=2x,DN =x,DE= 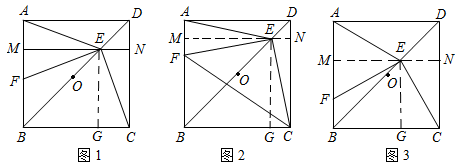 (责任编辑:admin) |
