|
☆☆☆ 点击下载试题 ☆☆☆  2018重庆重点中学数学模拟试题【精编Word版】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ （满分：150分，时间：120分钟） 一．选择题：（每小题4分，共48分） 1. 在0、﹣1、  、π四个实数中，最小的数是（ ）A．﹣1 B．0 C． D．π2. 下列瑜伽动作中，可以看成对称图形的是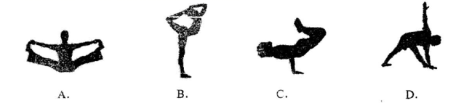（ ）  3. 列运算中正确的是（ ） A．（a2）3=a5 B．  C．a2+a2=a4 D．3x2﹣3x=x4. 下列调查中，最适合用普查方式的是（ ） 了解全市高三年级学生的睡眠质量 了解我校同学对国家设立雄安新区的看法 对端午节出游旅客上飞机前的安全检查 对电影“摔跤吧，爸爸”收视率的调查 5. 估算  的结果最接近的整数是（ ）A.3 B.4 C.5 D.6 6.若a2+b+5=0，则代数式3a2+3b+10的值为（ ） A．25 B．5 C．﹣5 D．0 7. 数y=  中，x的取值范围是（ ）x>2 B.x≠2 C. x≠0 D.x≠2且x≠0 8. △ADE~△ABC，且相似比为1:3，若△ADE的面积为5，则△ABC的面积为（ ） A.10 B.15 C.30 D.45 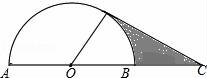 9. 如图，AB为半圆O的直径，点C在AB的延长线上，CD与半圆O相切于点D，且AB=2CD=8，则图中阴影部分的面积为（ ） A．  B．32﹣8π C．4﹣π D．8﹣2π在科幻电影中“银河护卫队”中，星球之间的穿梭往往靠宇宙飞船沿固定路径“空间跳跃”完成，如图所示：两个星球之间，它们的路径只有1条；三个星球之间的路径有3条，四个星球之间路径有6条，…，按此规律，则九个星球之间“空间跳跃”的路径有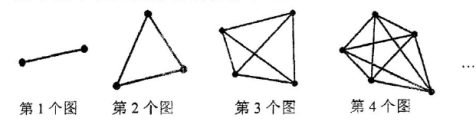（ ）  A.28条 B. 36条 C.45条 D.55条  11. 如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，斜坡AB的坡度  ，仰角 ，则山峰的高度CF约为（ ）米，（可用的参考数据： ）A.500 B. 518 C. 530 D. 580 12. 如果关于x的分式方程 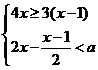 有整数解，且关于x的不等式组 有且只有四个整数解，那么符合条件的所有整数a的个数为（ ） A.0 B. 1 C. 2 D. 3二．填空题：(每小题4分,共24分) 13．中国首艘完全自主建造的航空母舰与近日正式下水，据悉这艘航母排水量将达到50000吨，直追伊丽莎白女王级航母，将50000这个数用科学记数法表示为 . 14．  = .15.如图，已知AB是⊙  的直径， ，则 的度数为 16、在学校演讲比赛中，十名选手的成绩统计图如图所示，则这10名选手成绩的平均分是 分。  17、甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地，乙车匀速前往A地，中途与甲车相遇后休息了一会儿，然后以原来的速度继续行驶直到A地。设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时）。y与x之间的函数图像如图所示，则乙车到达A地时甲车距B地的路程为______ 千米。  18、在正方形ABCD中，  ，E是边BC的中点，F是AB上一点，线段AE、CF交于点G，且CE=EG，将 沿CF翻折，使得点B落在点M，连接GM并延长交AD于点N，则 的面积为 。三．解答题：(每小题8分,共16分) 19．如图，△ABC与△DBE中，AC//DE，点B、C、E在同一直线上，AC，BD相交于点F.若∠BDE=85°，∠BAC=55°，∠ABD:∠DBE=3:4，求∠DBE的度数. 20．某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛，向学校学生征集书画作品，今年 3月份举行了“书画比赛”初赛，初赛成绩评定为A,B,C,D,E五个等级。该校七年级书法班全体学生参加了学校的比赛，并将比赛结果绘制成如下两幅不完整的统计图。请根据图中信息， 解答下列问题。 (1)该校七年级书法班共有 名学生; 扇形统计图中C等级所对应扇形的圆心角等于 度，并补全条形统计图; (2)A等级的4名学生中有2名男生，2名女生，现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛，请你用列表法或画树状图的方法，求出恰好选到1名男生和1名女生的概率。  四．解答题（每小题10分，共50分） 21.化简：（1）  （2）   22. 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数  的图像在第二象限交于点C, 轴 ,垂足为点E,  ， ， . （1）求反比例函数的解析式 （2）若点D是反比例函数图像在第四象限上的点，过点D作  轴，垂足为点F， 连接OD、BF，如果 ，求点D的坐标。23. 重庆某油脂公司生产销售菜籽油、花生油两种使用植物油. 已知花生的出油率为56%，是菜籽油的1.4倍，现有才子、花生共100吨，若想得到至少52吨植物油，则其中的菜籽至多有多少吨？ 在去年的销售中，菜籽油、花生油的售价分别为20元/升，30元/升，且销量相同.今年由于花生原材料价格上涨，花生油的售价比去年提高了a%，菜籽油的售价不变，总销量比去年降低a%，且菜籽油、花生油的销量均占今年总销量的  ，这样，预计今年的销售总额比去年下降 ，求a的值.24．如图，已知等腰Rt△ABC，∠ACB=90°，CA=CB，以BC为边向外作△CBD，连接AD，过点C作∠ACB的角平分线与AD交于点E，连接BE. 若AE=2，求CE的长度； 以AB为边向下作△AFB，∠AFB=60°，连接FE，求证：FA+FB=  . 25．一个形如  的五位自然数，（其中a表示该数的万位上的数字，b表示该数的千位上的数字，c表示该数的百位上的数字，d表示该位数的十位上的数字，e表示该数的个位上的数字，且 ，若有 且 ，则把该自然数叫做“对称数”，例如在自然数12321中，3=2+1，则12321是一个“对称数”.，同时规定，若该“对称数”的前两位数与后两位数的平方差是693的奇数倍，则称该“对称数”为“智慧对称数”.如在对称数43734中 则43734是一个“智慧对称数”。（1）将一个“对称数”的个位上与十位上的数字交换位置，同时，将千位上与万位上的数字交换位置，称交换前后的这两个“对称数”为一组“相关对称数”。例如：12321与21312为一组“相关对称数”，求证：任意的一组“相关对称数”之和是最小“对称数”的倍数; （2）求出所有的“智慧对称数”中的最大“智慧对称数”. 解答题（每小题12分，请按要求写出详细解答过程） 26．如图1，在平面直角坐标系中，抛物线  与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为点D.过点B作BC的垂线，交对称轴于点E.求证：点E与点D关于x轴对称； 点P为第四象限内的抛物线上的一动点，当△PAE的面积最大时，在对称轴上找一点M，在y轴上找一点N，使得OM+MN+NP最小，求此时点M的坐标及OM+MN+NP的最小值； 如图2，平移抛物线，使抛物线的顶点D在射线AD上移动，点D平移后的对应点为D′，点A的对应点为A′.设抛物线的对称轴于x轴交于点F，将△FBC沿BC翻折，使点F落在点F′处，在平面内找一点G，若以F′、G、D′、A′为顶点的四边形为菱形，求平移的距离. 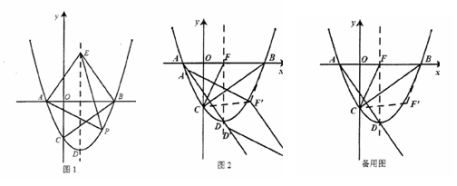 (责任编辑：admin) |