|
☆☆☆ 点击下载试题 ☆☆☆ 2018年抚州中考数学模拟试卷【word版 含答案详解】 由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看! 一、选择题(本大题共6小题,共18.0分) 下面几何体中,主视图与俯视图都是矩形的是 A. 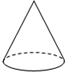 B. B. 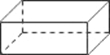 C. 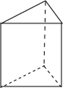 D. D. 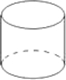 【答案】B 【解析】解:A、主视图是三角形,俯视图是圆及圆心,故此选项错误; B、主视图是矩形,俯视图是矩形,故此选项正确; C、主视图是矩形以及中间有一条虚线,俯视图是三角形,故此选项错误; D、主视图是矩形,俯视图是圆,故此选项错误; 故选B 主视图、俯视图是分别从物体正面、上面看,所得到的图形. 本题考查了几何体的三种视图,掌握定义是关键 菱形和矩形一定具备的性质是 A. 对角线互相平分 B. 对角线互相垂直 C. 对角线相等 D. 每条对角线平分一组对角 【答案】A 【解析】解:A、菱形和矩形的对角线都互相平分,所以A选项正确; B、菱形的对角线互相垂直平分,而矩形的对角线互相平分且相等,所以B选项错误; C、菱形的对角线互相垂直平分,而矩形的对角线互相平分且相等,所以C选项错误; D、菱形的对角线互相垂直平分且平分没组对角,而矩形的对角线互相平分且相等,所以D选项错误. 故选A. 根据菱形和矩形的性质对各选项分别进行判断. 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角 已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是 A. 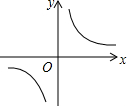 B. B. 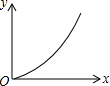 C.  D. D. 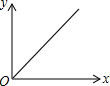 【答案】C 【解析】解: 故选:C. 由矩形的面积公式可得 本题主要考查反比例函数的图象,根据题意得出函数解析式及自变量的取值范围是确定函数图象的关键. 已知一元二次方程 A. 13 B. 11或13 C. 11 D. 12 【答案】B 【解析】解: 即 故选:B. 由一元二次方程 此题考查了因式分解法解一元二次方程、等腰三角形的性质以及三角形三边关系 如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形  A. 【答案】C 【解析】解:长为8cm、宽为4cm的矩形的面积是 留下的矩形 相似比是4: 因而面积的比是1:4, 因而留下矩形的面积是 故选:C. 利用相似多边形的对应边的比相等,对应角相等分析. 本题考查相似多边形的性质 已知二次函数 其中正确结论的个数是 A. 0 B. 1 C. 2 D. 3 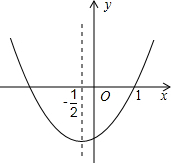 【答案】B 【解析】解: 得到: 又 故选:B. 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴确定b的符号,进而对所得结论进行判断. 主要考查二次函数图象与二次函数系数之间的关系,二次函数 二、填空题(本大题共1小题,共3.0分) 某地区为估计该地区黄羊的只数,先捕捉20只黄羊给它们分别作上标志,然后放回,待有标志的黄羊完全混合于黄羊群后,第二次捕捉60只黄羊,发现其中2只有标志 【答案】600 【解析】解: 故答案为600. 捕捉60只黄羊,发现其中2只有标志 本题考查了用样本估计总体的思想,统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体. 三、解答题(本大题共11小题,共88.0分) 计算: 【答案】解: 【解析】 本题考查的是实数的运算,熟记特殊角的三角函数值是解答此题的关键. 如图,矩形ABCD中, 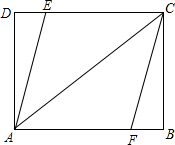 【答案】解; 设 则 则 解得: 则菱形的边长为: 周长为: 故菱形AFCE的周长为25. 【解析】 本题考查了矩形的性质和菱形的性质,解答本题的关键是则矩形对边平行且相等的性质以及菱形四条边相等的性质. 一个口袋中有4个完全相同的小球,把它们分别标号为 【答案】解: 它们的可能性相等 恰好摸到标号为2的小球的可能有1种
由上可知,随机摸取一个小球然后放回,再随机摸取一个小球,共16种可能性, 它们的可能性相等 两次摸取的小球标号的和为 【解析】 本题考查概率的求法;得到两次摸取的小球的标号的和为5的情况数是解决本题的关键;用到的知识点为:概率 关于x的一元二次方程 【答案】解: 解之得 答:m的值为 【解析】 本题考查了一元二次方程的求解,本题中代入 已知:如图,在 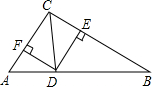 【答案】证明: 又 【解析】由题意可得,四边形CFDE是矩形,根据角平分线的性质得到 本题是考查正方形的判别方法,判别一个四边形为正方形主要根据正方形的概念,途经有两种: 如图,在 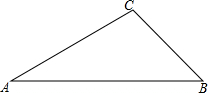 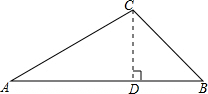 【答案】解:过点C作 【解析】过点C作 本题考查了解直角三角形,熟练应用三角函数的定义是解题的关键. 为打造“文化九中,书香校园”,阜阳九中积极开展“图书漂流”活动,旨在让全体师生共建共享,校团委学生处在对上学期学生借阅登记簿进行统计时发现,在4月份有1000名学生借阅了名著类书籍,5月份人数比4月份增加 【答案】解: 5月份借阅了名著类书籍的人数是: 则6月份借阅了名著类书籍的人数为: 解得: 答:从4月份到6月份全校借阅名著类书籍的学生人数的平均增长率为 【解析】 本题是一道数学应用题中的增长率问题的实际问题,考查了列一元二次方程解实际问题的运用及一元二次方程的解法的运用,解答中对结果验根是否符合题意是解答的关键. 如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得 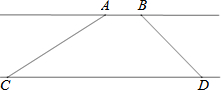  【答案】解:如图,分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为h. 在 在 答:两条河岸之间的距离约为18米. 【解析】分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为 本题考查了解直角三角形的应用,通过作辅助线构造直角三角形,用含h的代数式分别表示出CE与FD是解题的关键. 抛物线 【答案】解: 把点 【解析】 本题考查二次函数性质,解题的关键是灵活掌握待定系数法,学会利用方程组求函数图象交点坐标,属于中考常考题型. 如图,一次函数 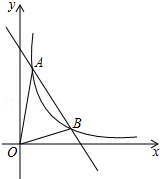 【答案】解: 把 【解析】 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式 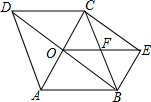 如图,点O是菱形ABCD对角线的交点, 【答案】  【解析】 本题考查了菱形的性质和勾股定理 (责任编辑:admin) |
||||||||||||||||||||||||||||||||||||||
