|
☆☆☆ 点击下载试题 ☆☆☆  2018临沧中考数学模拟真题【精编Word版含答案及解析】 由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、填空题（本大题共6小题，请将答案书写在答题卡相应题号位置，每小题3分，满分18分） 1．（3分）若x2=3，则x= ． 2．（3分）已知点A（﹣2，a）与点B（b，  3）关于原点对称，则a﹣b= 3．（3分）已知二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2）和（4，2），则此抛物线的对称轴是直线 4．（3分）一个不透明的袋子里装有3个白球和4个红球，小明任意摸一个，摸到红球的概率为 5．（3分）一个扇形的弧长是20πcm，面积是240πcm2，则这个扇形的圆心角是 度． 6．（3分）如图是小明用火柴搭的1条、2条、3条“金鱼”……，则搭50条“金鱼”需要火柴 根．  二、选择题（本大题共8小题，每小题只有一个正确选项，请将答案中书写在答题卡相应题号位置，每小题4分，满分32分） 7．（4  分）下列汽车标志中，既是轴对称图形，又是中心对称图形的是（ ）A．  B．  C． D． 8．（4分）二次函数y=﹣2x2+4x+3的图象的顶点坐标是（ ） A．（1，5） B．（﹣1，5） C．（1，3） D．（﹣1，3） 9．（4分）如图，在⊙O中，弦AB的长为16cm，圆心O到AB的距离为6cm，则⊙O的半径是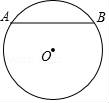（ ）  A．6cm B．10cm C．8cm D．20cm 10．（4分）二次函数y=ax2+bx+c的图象如图所示，则下列关系式错误的是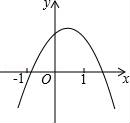（ ）  A．a＜0 B．b＞0 C．b2﹣4ac＞0 D．a+b+c＜0 11．（4分）下列事件中是必然事件的是（ ） A．随意掷两枚均匀的骰子，朝上面的点数之和是5 B．投掷一枚硬币，正面向上 C．打开电视，正在播放动画片 D．3个人分成两组，一定有2个人分在一组 12．（4分）向阳村2015年的人均收入为12000元，2017年的人均收入为14520元，设这两年向阳村的人均收入的年平均增长百分率为x，那么下面列出的方程正确的是（ ） A．12000x2=14520 B．12000（1+x）2=14520 C．12000（1+x2）=14520 D．12000（1+x%）=14520 13．（4分）如图，PA，PB分别与⊙O相切于A、B两点，∠P=80°，则∠C为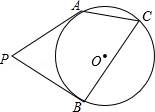（ ）  A．160° B．100° C．50° D．80° 14．（4分）把抛物线y=﹣2x2+4x+1的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是（ ） A．y=﹣2（x﹣1）2+6 B．y=﹣2（x﹣1）2﹣6 C．y=﹣2（x+1）2+6 D．y=﹣2（x+1）2﹣6 三、简答题（本大题共9小题，请将解答书写在答题卡相应题号位置，满分70分） 15．（10分）解方程： （1）5x2﹣3x=x+1 （2）x2﹣8x+1=0 16．（7分）如图，A、B是⊙O上的两点，∠AOB=120°，C是  的中点．求证：四边形AOBC是菱形． 17．（7分）如图，某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草．要使每一块花草的面积都为78m2，那么通道的宽应设计成多少m？  18．（6分）求证：无论p取何值，方程（x﹣3）（x﹣2）﹣p2=0总有两个不等的实数根 19．（7分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4） （1）请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1； （2）请画出△ABC关于原点O成中心对称的图形△A2B2C2； （3）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．  20．（8分）佳佳父母的服装店开业了，销售一种服装，进价40元/件，现每件以60元出售，一星期卖出300件，佳佳对父母的服装店很感兴趣，因此，她对市场作了调查．调查结果如下：如果涨价，每涨1元，每星期少卖出10件；请问：佳佳如何定价才能使利润最大？最大利润是多少？ 21．（8分）某校举办艺术节，其中A班和B班的节目总成绩并列第一，学校决定从A、B两班中选派一个班代表学校参加全省比赛，B班班长想法是：用八张扑克牌，将数字为1，2，3，5的四张牌给A班班长，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：A班班长和B班班长从各自的四张牌中随机抽出一张，然后将抽出的两张扑克牌数字相加，如果和为偶数，则A班去；如果和为奇数，则B班去． （1）请用树状图或列表的方法求A班去参赛的概率． （2）B班班长设计的游戏规则公平吗？若公平，请说明理由；若不公平，请你 设计一种公平的游戏规则．22．（8分）如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE． （1）求证：DE是⊙O的切线； （2）若AE=6，∠D=30°，求图中阴影部分的面积．  23．（9分）在直角坐标平面中，O为坐标原点，二次函数y=﹣x2+（k﹣1）x+4的图象与y轴交于点 A，与x轴的负半轴交于点B，且S△OAB=6．（1）求点A与点B的坐标； （2）求此二次函数的解析式； （3）如果点P在x轴上，且△ABP是等腰三角形，求点P的坐标．  2018临沧中考数学模拟真题参考答案与试题解析 一、填空题（本大题共6小题，请将答案书写在答题卡相应题号位置，每小题3分，满分18分） 1．（3分）若x2=3，则x=  ．【解答】解：∵x2=3， ∴x=±  ，故答案为：  ．2．（3分）已知点A（﹣2，a）与点B（b，3）关于原点对称，则a﹣b= ﹣5 【解答】解：由题意，得： a=﹣3，b=2， a﹣b=﹣3﹣2=﹣5， 故答案为：﹣5． 3．（3分）已知二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2）和（4，2），则此抛物线的对称轴是直线 x=  4．【解答】解： ∵抛物线y=ax2+bx+c（a≠0）经过点（﹣1，2）和（4，2）， ∴对称轴为x=  ，故答案为：x=  ．4．（3分）一个不透明的袋子里装有3个白球和4个红球，小明任意摸一个，摸到红球的概率为  【解答】解：∵共有3+4=7个球，红球有4个， ∴摸出的球是红球的概率是 ；故答案为： ．5．（3分）一个扇形的弧长是20πcm，面积是240πcm2，则这 个扇形的圆心角是 150 度．【解答】解：扇形的面积公式=  lr=240πcm2，解得：r=24cm， 又∵l=  =20πcm，∴n=150°． 故答案为：150． 6．（3分）如图是小明用火柴搭的1条、2条、3条“金鱼”……，则搭50条“金鱼”需要火柴 302 根．  【解答】解：第1条金鱼用了8根火柴； 第2条金鱼用了8+6=14根火柴； 第3条金鱼用了8+2×6=20根火柴； … 第n条金鱼用了8+6（n﹣1）=6n+2根火柴， 所以搭50条“金鱼”需要火柴6×50+2=302根， 故答案为：302． 二、选择题（本大题共8小题，每小题只有一个正确选项，请将答案中书写在答题卡相应题号位置，每小题4 分，满分32分）7．（4分）下列汽车标志中，既是轴对称图形，又是中心对称图形的是（ ） A．  B． C． D． 【解答】解：A、不是轴对称图形，也不是中心对称图形，故此选项错误； B、是轴对称图 形，也是中心对称图形，故此选项正确；C、C、是轴对称图形，不是中心对称图形，故此选项错误； D、是轴对称图形，不是中心对称图形，故此选项错误． 故选：B． 8．（4分）二次函数y=﹣2x2+4x+3的图象的顶点坐标是（ ） A．（1，5） B．（﹣1，5） C．（1，3） D．（﹣1，3） 【解答】解：y=﹣2x2+4x+3=﹣2（x﹣1）2+5， ∴该函数的顶点坐标是（1，5）， 故选：A． 9．（4分）如图，在⊙O中，弦AB的长为16cm，圆心O到AB的距离为6cm，则⊙O的半径是（ ）  A．6cm B．10cm C．8cm D．20cm 【解答】解：过点O作OE⊥AB于点E，连接OC， ∵弦AB的长为16cm，圆心O到AB的距离为6cm ∴OE=6cm，AE=  AB=8cm，在Rt△AOE中，根据勾股定理得，OA=  =10c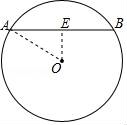m故选：B．  10．（4分）二次函数y=ax2+bx+c的图象如图所示，则下列关系式错误的是（ ）  A．a＜0 B．b＞0 C．b2﹣4ac＞0 D．a+b+c＜0 【解答】解：A、抛物线开口向下，则a＜0，所以A选项的关系式正确； B、抛物线的对称轴在y轴的右侧，a、b异号，则b＞0，所以B选项的关系式正确； C、抛物线与x轴有2个交点，则△=b2﹣4ac＞0，所以D选项的关系式正确； D、当x=1时，y＞0，则a+b+c＞0，所以D选项的关系式错误． 故选：D． 11．（4分）下列事件中是必然事件的是（ ） A．随意掷两枚均匀的骰子，朝上面的点数之和是5 B．投掷一枚硬币，正面向上 C．打开电视，正在播放动画片 D．3个人分成两组，一定有2个人分在一组 【解答】解：A、随意掷两枚均匀的骰子，朝上面的点数之和是5是随机事件，故本选项错误； B、投掷一枚硬币，正面向上是随机事件，故本选项错误； C、打开电视，正在播放动画片是随机事件，故本选项错误； D、3个人分成两组，一定有2个人分在一组是必然事件，故本选项正确； 故选：D． 12．（4分）向阳村2015年的人均收入为12000元，2017年的人均收入为14520元，设这两年向阳村的人均收入的年平均增长百分率为x，那么下面列出的方程正确的是（ ） A．12000x2=14520 B．12000（1+x）2=14520 C．12000（1+x2）=14520 D．12000（1+x%）=14520 【解答】解：设这两年向阳村的人均收入的年平均增长百分率为x， 由题意可得，12000（1+x）2=14520， 故选：B． 13．（4分）如图，PA，PB分别与⊙O相切于A、B两点，∠P=80°，则∠C为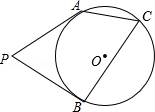（ ）  A．160° B．100° C．50° D．80° 【解答】解：连接OA、OB， ∵直线PA、PB分别与⊙O相切于点A、B， ∴OA⊥PA，OB⊥PB， ∵∠P=80°， ∴∠AOB=100°， ∵C是⊙O上一点， ∴∠ACB=50°． 故选：C 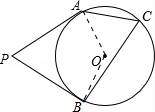． 14．（4分）把抛物线y=﹣2x2+4x+1的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是（ ） A．y=﹣2（x﹣1）2+6 B．y=﹣2（x﹣1）2﹣6 C．y=﹣2（x+1）2+6 D．y=﹣2（x+1）2﹣6 【解答】解：原抛物线  的顶点坐标为（1，3），向左平移2个单位，再向上平移3个单位得到新抛物线的顶点坐标为（﹣1，6）．可设新抛物线的解析式为：y=﹣2（x﹣h）2+k，代入得：y=﹣2（x+1）2+6．故选C．三、简答题（本大题共9小题，请将解答书写在答题卡相应题号位置，满分70分） 15．（10分）解方程： （1）5x2﹣3x=x+1 （2）x2﹣8x+1=0 【解答】解：（1）5x2﹣3x=x+1， 5x2﹣4x﹣1=0， （5x+1）（x﹣1）=0， 5x+1=0，x﹣1=0， x1=﹣  ，x2=1；（2）x2﹣8x+1=0 x2﹣8x=﹣1， x2﹣8x+16=﹣1+16， （x﹣4）2=15， x﹣4=  ，x1=4+  ，x2=4﹣．16．（7分）如图，A、B是⊙O上的两点，∠AOB=120°，C是 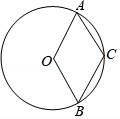 的中点．求证：四边形AOBC是菱形． 【解答】证明：连OC，如图， ∵C是 的中点，∠AOB=l20°∴∠AOC=∠BOC=60°， 又∵OA=OC=OB， ∴△OAC和△OBC都是等边三角形， ∴AC=OA=OB=BC， ∴四边形OACB是菱形．  17．（7分）如图，某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草．要使每一块花草的面积都为78m2，那么通道的宽应设计成多少m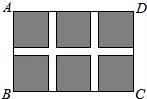？  【解答】解：设道路的宽为xm，由题意得： （30﹣2x）（20﹣x）=6×78， 整理得：（x﹣2）（x﹣33）=0， 解得x=2或x=33舍去）， 答：通道应设计成2米． 18．（6分）求证：无论p取何值，方程（x﹣3）（x﹣2）﹣p2=0总有两个不等的实数根 【解答】证明： ∵（x﹣3）（x﹣2）﹣p2=0， ∴x2﹣5x+6﹣p2=0， ∴△=（﹣5）2﹣4（6﹣p2）=25﹣24+4p2=4p2+1＞0恒成立， ∴无论p取何值，方程（x﹣3）（x﹣2）﹣p2=0总有两个不等的实数根． 19．（7分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4） （1）请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1； （2）请画出△ABC关于原点O成中心对称的图形△A2B2C2； （3）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标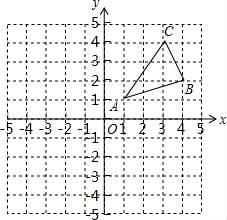．  【解答】解：（1）如图1所示： （2）如图2所示： （3）找出A的对称点A′（1，﹣1）， 连接BA′，与x轴交点即为P； 如图3所示：点P坐标为（2，0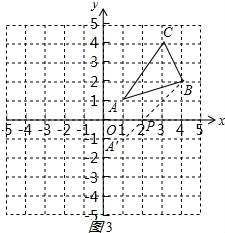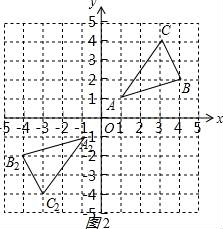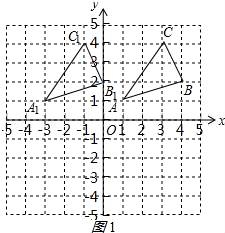）．    20．（8分）佳佳父母的服装店开业了，销售一种服装，进价40元/件，现每件以60元出售，一星期卖出300件，佳佳对父母的服装店很感兴趣，因此，她对市场作了调查．调查结果如下：如果涨价，每涨1元，每星期少卖出10件；请问：佳佳如何定价才能使利润最大？最大利润是多少？ 【解答】解：设每星期所获利润为y，若每件涨价x元，根据题意得， y= （60+x﹣40）（300﹣10x）=﹣10x2+100x+6000 =﹣10（x﹣5）2+6250（0≤x≤30）， ∵a=﹣10＜0， ∴x=5，y有最大值6250， 即定价为65元时，所获利润最大，最大利润为6250元． 21．（8分）某校举办艺术节，其中A班和B班的节目总成绩并列第一，学校决定从A、B两班中选派一个班代表学校参加全省比赛，B班班长想法是：用八张扑克牌，将数字为1，2，3，5的四张牌给A班班长，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：A班班长和B班班长从各自的四张牌中随机抽出一张，然后将抽出的两张扑克牌数字相加，如果和为偶数，则A班去；如果和为奇数，则B班去． （1）请用树状图或列表的方法求A班去参赛的概率． （2）B班班长设计的游戏规则公平吗？若公平，请说明理由；若不公平，请你设计一种公平的游戏规则． 【解答】解：（1）所有可能的结果如下表：
一共16种结果，每各结果出现的可能性相同 P和为偶数的概率=  = ；所以A班去参赛的概率为： ；（2）游戏不公平， 理由：由（1）列表的结果可知：A班去的概率为 ，B班去的概率为 ，所以游戏不公平，对B班有利．游戏规则改为：若和为偶数则A班得5分，若和为奇数则B班得3分，抽取8次后看总得分，分数高的去，则游戏是公平的． （注：第（2）小题  规则修改不惟一，只要使得A、B两班的概率相等，即可得满分）22．（8分）如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE． （1）求证：DE是⊙O的切线； （2）若AE=6，∠D=30°，求图中阴影部分的面积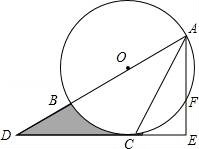．  【解答】（1）证明：连接OC， ∵OA=OC， ∴ ∠OAC=∠OCA，∵AC平分∠BAE， ∴∠OAC=∠CAE， ∴∠OCA=∠CAE， ∴OC∥AE， ∴∠OCD=∠E， ∵AE⊥DE， ∴∠E=90°， ∴∠OCD=90°， ∴OC⊥CD， ∵点C在圆O上，OC为圆O的半径， ∴CD是圆O的切线； （2） ∵在Rt△AED中，∠D=30°，AE=6， ∴AD=2AE=12， 在Rt△AED中，∵∠D=30°， ∴DO=2OC=DB+OB=DB+OC， ∴DB=OB=OC=  AD=4，DO=8，∴CD=  ，∴S△OCD=  ，∵∠D=30°，∠OCD=90°， ∴∠DOC=60°， ∴S扇形OBC=  ×π×OC2= ，∵S阴影=S△COD﹣S扇形OBC ∴S阴影=8  ﹣ ，∴阴影部分的面积为8 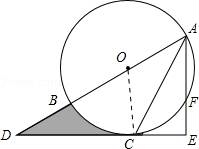 ﹣ ． 23．（9分）在直角坐标平面中，O为坐标原点，二次函数y=﹣x2+（k﹣1）x+4的图象与y轴交于点A，与x轴的负半轴交于点B，且S△OAB=6． （1）求点A与点B的坐标； （2）求此二次函数的解析式； （3）如果点P在x轴上，且△ABP是等腰三角形，求点P的坐标．  【解答】解：（1）由解析式可知，点A的坐标为（0，4）．（1分） ∵S△OAB=  ×BO×4=6BO=3．所以B（3，0）或（﹣3，0）， ∵二次函数与x轴的负半轴交于点B， ∴点B的坐标为（﹣3，0）；（2分） （2）把点B的坐标（﹣3，0）代入y=﹣x2+（k﹣1）x+4， 得﹣（﹣3）2+（k﹣1）×（﹣3）+4=0． 解得k﹣1=﹣  ．（4分）∴所求二次函数的解析式为y=﹣x2﹣ x+4．（5分）（3）因为△ABP是等腰三角形， 所以：①如图1，当AB=AP时，点P的坐标为（3，0）（6分） ②如图2，当AB=BP时，点P的坐标为（2，0）或（﹣8，0）（8分） ③如图，3，当AP=BP时，设点P的坐标为（x，0） 根据题意，得 =|x+3|．解得x=  ．∴点P的坐标为（  ，0）（10分）综上所述，点P的坐标为（3，0），（2，0），（﹣8，0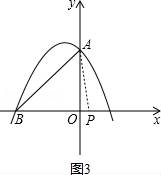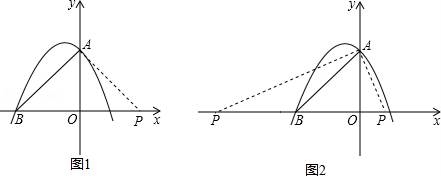），（ ，0）．  (责任编辑：admin) |