|
☆☆☆ 点击下载试题 ☆☆☆  2018北京101中学中考数学冲刺试卷【word版 含答案】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题：本大题共8小题，共40分. 1. 在复平面内，复数  对应的点位于（ ）A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2. 执行如图所示的程序框图，输出的结果为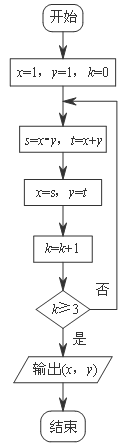（ ）  A.  B.  C.  D.  3. 一位母亲记录了自己儿子3～9岁的身高数据（略），由此建立的身高与年龄的回归模型为y=7.19x＋73.93，用这个模型预测这个孩子10岁时的身高，则正确的叙述是（ ） A. 身高一定是145.83cm B. 身高在145.83cm以上 C. 身高在145.83cm左右 D. 身高在145.83cm以下 4. 用反证法证明命题“设a，b为实数，则方程x3＋ax＋b=0至少有一个实根”时，要做的假设是（ ） A. 方程x3＋ax＋b=0没有实根 B. 方程x3＋ax＋b=0至多有一个实根 C. 方程x3＋ax＋b=0至多有两个实根 D. 方程x3＋ax＋b=0恰好有两个实根 5. 若  ， ， ，则（ ）A. b＞c＞a B. b＞a＞c C. a＞b＞c D. c＞a＞b 6. 下列函数中既是奇函数又在区间（0，+∞）上单调递减的是（ ） A.  B. y=ln（-x） C. y=x3 D.  7. 下面四个条件中，使a>b成立的充分不必要的条件是（ ） A. a>b＋1 B. a>b－1 C. a2>b2 D. a3>b3 8. 观察下列各式：a＋b＝1，a2＋b2＝3，a3＋b3＝4，a4＋b4＝7，a5＋b5＝11，…，则a10＋b10＝（ ） A. 28 B. 76 C. 123 D. 199 二、填空题：本大题共6小题，共30分. 9. 命题“∀x∈R，|x－2|＋|x－4|>3”的否定是__________________________________. 10. 设复数z＝1＋2i（i是虚数单位），则|z|＝________. 11. 设  的导函数为 ，则 的值为__________. 12. 若对任意m∈R，直线x＋y＋m＝0都不是曲线f（x）＝x3－ax的切线，则实数a的取值范围是________. 13. 已知函数f（＋2）＝x＋2，则函数f（x）的值域为________. 14. 如图，在平面直角坐标系的格点（横、纵坐标均为整数的点）处：点（1，0）处标b1，点（1，-1）处标b2，点（0，-1）处标b3，点（-1，-1）处标b4，点（-1，0）处标b5，点（-1，1）处标b6，点（0，1）处标b7，…，以此类推，则b2017处的格点的坐标为________. 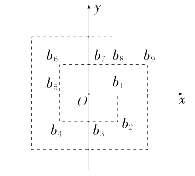 三、解答题：本大题共5题，共50分. 15. 已知P＝{x|x2－8x－20≤0}，S＝{x|1－m≤x≤1＋m}. （1）是否存在实数m，使x∈P是x∈S的充要条件，若存在，求出m的范围； （2）是否存在实数m，使x∈P是x∈S的必要条件，若存在，求出m的范围. 16. 若复数  满足 ，其中 为虚数单位，求复数 .17. 设函数f（x）＝x3＋ax2＋bx＋1的导数  满足 ， ，其中常数a，b∈R.（1）求曲线y＝f（x）在点（1，f（1））处的切线方程； （2）设  ，求函数g（x）的极值. 18. 已知函数  ，x∈[－1,1]，函数 ,a∈R的最小值为h（a）. （1）求h（a）的解析式； （2）是否存在实数m，n同时满足下列两个条件：①m>n>3；②当h（a）的定义域为[n，m]时，值域为[n2，m2]？若存在，求出m，n的值；若不存在，请说明理由. 19. 如图，在平面直角坐标系内从点P1（0,0）作x轴的垂线交曲线y＝ex于点Q1（0,1），曲线在Q1点处的切线与x轴交于点P2.再从P2作x轴的垂线交曲线于点Q2，依次重复上述过程得到一系列点：P1，Q1；P2，Q2；…；Pn，Qn，记 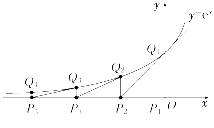 点的坐标为（ ,0）（k＝1,2，…，n）.  （1）试求 与 的关系（k＝2，…，n）；（2）求|P1Q1|＋|P2Q2|＋|P3Q3|＋…＋|PnQn|. 2018北京101中学中考数学冲刺试卷参考答案 一、选择题：本大题共8小题，共40分.
二、填空题：本大题共6小题，共30分. 9. ∃x∈R，|x－2|＋|x－4|≤3 10. __________________ 11. _________  __________ 12. _______（－∞，1）________13. ______[0，＋∞）_________ 14. ______（15，22 ） __________ 三、解答题：本大题共5题，共50分. 15. （1）由x2－8x－20≤0得－2≤x≤10，∴P＝{x|－2≤x≤10}， ∵x∈P是x∈S的充要条件，∴P＝S， ∴∴这样的m不存在； （2）由题意x∈P是x∈S的必要条件，则S⊆P， ∴∴m≤3. 综上，可知m≤3时，x∈P是x∈S的必要条件. 16. 解:设  ，则 17. 解：（1）∵f（x）＝x3＋ax2＋bx＋1，∴f′（x）＝3x2＋2ax＋b， 则解得 ∴f（x）＝x3－x2－3x＋1，∴f（1）＝－，f′（1）＝－3， ∴y＝f（x）在（1，f（1））处的切线方程为 y－＝－3（x－1），即6x＋2y－1＝0； （2）由（1）知g（x）＝（3x2－3x－3）e－x， ∴g′（x）＝（－3x2＋9x）e－x， 令g′（x）＝0，即（－3x2＋9x）e－x＝0，得x＝0或x＝3， 当x∈（－∞，0）时，g′（x）<0， 故g（x）在（－∞，0）上单调递减. 当x∈（0,3）时，g′（x）>0，故g（x）在（0,3）上单调递增. 当x∈（3，＋∞）时，g′（x）<0， 故g（x）在（3，＋∞）上单调递减. 从而函数g（x）在x＝0处取得极小值g（0）＝－3， 在x＝3处取得极大值g（3）＝15e－3. 18. 解：（1）h（a）＝ （2）当a≥3时，h（a）＝－6a＋12，故m>n>3时，h（a）在[n，m]上为减函数， 所以h（a）在[n，m]上的值域为[h（m），h（n）]. 由题意，则有⇒，两式相减得6n－6m＝n2－m2，又m≠n，所以m＋n＝6，这与m>n>3矛盾，故不存在满足题中条件的m，n的值. 19. 解：（1）设点Pk－1的坐标是（xk－1,0）， ∵y＝ex，∴y′＝ex， ∴Qk－1（xk－1，exk－1），在点Qk－1（xk－1，exk－1）处的切线方程是y－exk－1＝exk－1（x－xk－1），令y＝0，则 xk＝xk－1－1（k＝2，…，n）； （2）∵x1＝0，xk－xk－1＝－1， ∴xk＝－（k－1）， ∴|PkQk|＝exk＝e－（k－1）， 于是有|P1Q1|＋|P2Q2|＋|P3Q3|＋…＋|PnQn| ＝1＋e－1＋e－2＋…＋e－（n－1） ＝＝， 即|P1Q1|＋|P2Q2|＋|P3Q3|＋…＋|PnQn|＝.  (责任编辑：admin) |