2020中考数学知识点：分式_中考网-中考真题答案下载-中考试题库-中考成绩查询-知识点学习方法与技巧补课解题技巧学习计划表总结-中考查分网-中考网-中考资源网-中学学科网

(3)约分时，分子与分母不是乘积形式，不能约分.
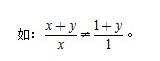分式12.jpg

    3.求最简公分母的方法是：
    (1)将各个分母分解因式;
    (2)找各分母系数的最小公倍数;
    (3)找出各分母中不同的因式，相同因式中取次数较高的，满足(2)(3)的因式之积即为各分式的最简公分母(求最简公分母在分式的加减运算和解分式方程时起非常重要的作用)。
    二、分式的运算：
    1.分式的加减法法则：
    (1)同分母的分式相加减，分母不变，把分子相加;
    (2)异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法则进行计算。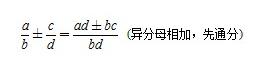
     分式13.jpg

2.分式的乘除法法则：两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母;两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘。
QQ截图20180813105836.jpg

    4.分式的混合运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的。
    5.对于分式化简求值的题型要注意解题格式，要先化简，再代人字母的值求值。
    可化为一元一次方程的分式方程知识点总结
    一.列分式方程解应用题的步骤：
    列分式方程解应用题的一般步骤为：
    (1)设未知数：若把题目中要求的未知数直接用字母表示出来，则称为直接设未知数，否则称间接设未知数;
    (2)列代数式：用含未知数的代数式把题目中有关的量表示出来，必要时作出示意图或列成表格，帮助理顺各个量之间的关系;
    (3)列出方程：根据题目中明显的或者隐含的相等关系列出方程;
    (4)解方程并检验;
    (5)写出答案。
    二.列分式方程解应用题的注意事项：
    由于列方程解应用题是对实际问题的解答，所以检验时除从数学方面进行检验外，还应考虑题目中的实际情况，凡不符合实际的，应舍去。
    常见考法
    列分式方程解应用题是中考命题的热点，命题广泛联系实际，题型新颖开放，但只要把握列分式方程解应用题的几个步骤，解决起来仍不困难。
    误区提醒
    (1)单位不统一;
    (2)解完分式方程后忽略“双检”。
     新初三快扫码关注



     中考网微信公众号



     每日推送学习技巧，学科知识点



     助你迎接2020年中考！

    一、约分与通分：
    1.约分：把一个分式的分子和分母的公因式约去，这种变形称为分式的约分;
    分式约分：将分子、分母中的公因式约去，叫做分式的约分。分式约分的根据是分式的基本性质，即分式的分子、分母都除以同一个不等于零的整式，分式的值不变。
    约分的方法和步骤包括：
    (1)当分子、分母是单项式时，公因式是相同因式的最低次幂与系数的最大公约数的积;
    (2)当分子、分母是多项式时，应先将多项式分解因式，约去公因式。
    2.通分：根据分式的基本性质，异分母的分式可以化为同分母的分式，这一过程称为分式的通。
    分式通分：将几个异分母的分式化成同分母的分式，这种变形叫分式的通分。
    (1)当几个分式的分母是单项式时，各分式的最简公分母是系数的最小公倍数、相同字母的较高次幂的所有不同字母的积;
    (2)如果各分母都是多项式，应先把各个分母按某一字母降幂或升幂排列，再分解因式，找出最简公分母;
    (3)通分后的各分式的分母相同，通分后的各分式分别与原来的分式相等;
    (4)通分和约分是两种截然不同的变形.约分是针对一个分式而言，通分是针对多个分式而言;约分是将一个分式化简，而通分是将一个分式化繁。
    注意：
    (1)分式的约分和通分都是依据分式的基本性质;
    (2)分式的变号法则：分式的分子、分母和分式本身的符号，改变其中的任何两个，分式的值不变。
    分式11.jpg
    (3)约分时，分子与分母不是乘积形式，不能约分.
    分式12.jpg
    3.求最简公分母的方法是：
    (1)将各个分母分解因式;
    (2)找各分母系数的最小公倍数;
    (3)找出各分母中不同的因式，相同因式中取次数较高的，满足(2)(3)的因式之积即为各分式的最简公分母(求最简公分母在分式的加减运算和解分式方程时起非常重要的作用)。
    二、分式的运算：
    1.分式的加减法法则：
    (1)同分母的分式相加减，分母不变，把分子相加;
    (2)异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法则进行计算。
    分式13.jpg
    2.分式的乘除法法则：两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母;两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘。
    QQ截图20180813105836.jpg
    4.分式的混合运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的。
    5.对于分式化简求值的题型要注意解题格式，要先化简，再代人字母的值求值。
    可化为一元一次方程的分式方程知识点总结
    一.列分式方程解应用题的步骤：
    列分式方程解应用题的一般步骤为：
    (1)设未知数：若把题目中要求的未知数直接用字母表示出来，则称为直接设未知数，否则称间接设未知数;
    (2)列代数式：用含未知数的代数式把题目中有关的量表示出来，必要时作出示意图或列成表格，帮助理顺各个量之间的关系;
    (3)列出方程：根据题目中明显的或者隐含的相等关系列出方程;
    (4)解方程并检验;
    (5)写出答案。
    二.列分式方程解应用题的注意事项：
    由于列方程解应用题是对实际问题的解答，所以检验时除从数学方面进行检验外，还应考虑题目中的实际情况，凡不符合实际的，应舍去。
    常见考法
    列分式方程解应用题是中考命题的热点，命题广泛联系实际，题型新颖开放，但只要把握列分式方程解应用题的几个步骤，解决起来仍不困难。
    误区提醒
    (1)单位不统一;
    (2)解完分式方程后忽略“双检”。
     (责任编辑：admin)

搜索

热门标签:

2020中考数学知识点：分式