|
从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线。角平分线是在角的型内及形上,到角两边距离相等的点的轨迹。  作法 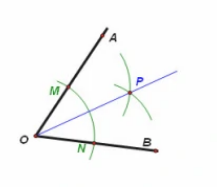 方法一:1.以点O为圆心,以任意长为半径画弧,两弧交角AOB两边 于点M,N。 2.分别以点M,N为圆心,以大于1/2MN的长度为半径画弧, 两弧交于点P。 3.作射线OP。 射线OP即为所求。 证明:连接PM,PN 在△POM和△PON中 ∵OM=ON,PM=PN,PO=PO ∴△POM≌△PON(SSS) ∴∠POM=∠PON,即射线OP为角AOB的角平分线 当然,角平分线的作法有很多种。下面再提供一种尺规作图的方法供参考。 方法二:1.在两边OA、OB上分别截取OM、OC和ON、OD,使OM=ON,OC=OD; 2.连接CN与DM,相交于P; 3.作射线OP。 射线OP即为所求。 (责任编辑:admin) |
