|
给定不在一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最短的点的位置。△ABC三条边的张角都等于120°,即满足∠APB=∠BPC=∠CPA=120°的点P就是到点A,B,C的距离之和最小的点。  费马问题 费马问题有多种不同的解法,最简单快捷的还是纯几何解法。 几何方法解决费马问题,一种思想是把问题中的三条线段PA,PB,PC“加”在一起或者说拼接在一起,最好是把它们拼接成连接两个定点的一条折线。因为两点之间线段最短,就能很快地确定PA+PB+PC的最小值。利用旋转变换能成功地把费马问题中的三条线段以一种非常自然的方式“加到一起”。 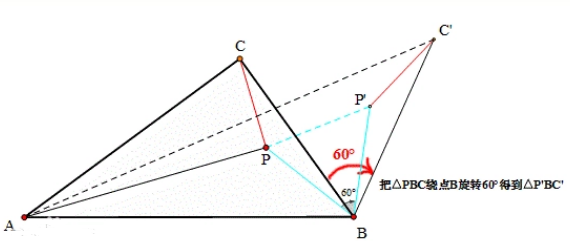 只要把△BPC绕点B旋转60°(如上图所示),设点P转到了点P',点C转到了点C',于是就有 PC=P'C',PB=PP'(因为△PBP'是等边三角形) 因此就有 PA+PB+PC=PA+PP'+P'C' 上式的右边是连接点A和点C'的一段折线的距离,它一定大于或等于线段AC'的长度,所以我们就得到了不等式: PA+PB+PC=PA+PP'+P'C'≥AC' 显然,如果上面的不等式能取到等号,那么这时候的点P就是到点A,B,C距离之和最小的点,也就是费马点。 (责任编辑:admin) |
