|
取AC的中点E,连接DE。取BC的中点D。∵AD是斜边BC的中线,∴BD=CD=1/2BC,∵E是AC的中点,∴DE是△ABC的中位线,∴DE//AB(三角形的中位线平行于底边)∴∠DEC=∠BAC=90°(两直线平行,同位角相等)∴DE垂直平分AC,∴AD=CD=1/2BC(垂直平分线上的点到线段两端距离相等)。  证明直角三角形斜边中线等于斜边一半 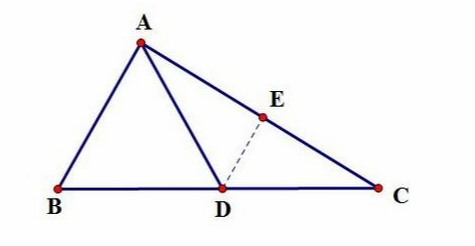 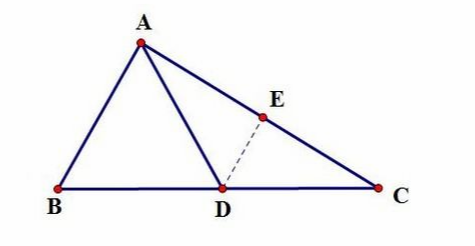 取AC的中点E,连接DE。取BC的中点D ∵AD是斜边BC的中线, ∴BD=CD=1/2BC, ∵E是AC的中点, ∴DE是△ABC的中位线, ∴DE//AB(三角形的中位线平行于底边) ∴∠DEC=∠BAC=90°(两直线平行,同位角相等) ∴DE垂直平分AC, ∴AD=CD=1/2BC(垂直平分线上的点到线段两端距离相等)。 直角三角形的特殊性质 1、直角三角形两直角边的平方和等于斜边的平方。如图,∠BAC=90°,则AB²+AC²=BC²(勾股定理) 2、在直角三角形中,两个锐角互余。如图,若∠BAC=90°,则∠B+∠C=90° 3、直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。该性质称为直角三角形斜边中线定理。 4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。 (责任编辑:admin) |
