|
把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数。  有理数和无理数的区别 1、两者概念不同。 有理数是整数和分数的统称,正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因此有理数的数集可分为正有理数、负有理数和零。 无理数,也称为无限不循环小数。简单来说,无理数就是10进制下的无限不循环小数,如圆周率、根号2等。 2、两者性质不同。 有理数的性质是一个整数a和一个正整数b的比,例如3比8,通常为a比b。 无理数的性质是由整数的比率或分数构成的数字。 3、两者范围不同。 有理数集是整数集的扩张,在有理数集内,加法、减法、乘法、除法4种运算均可进行。 而无理数是指实数范围内,不能表示成两个整数之比的数。 有理数(Q) 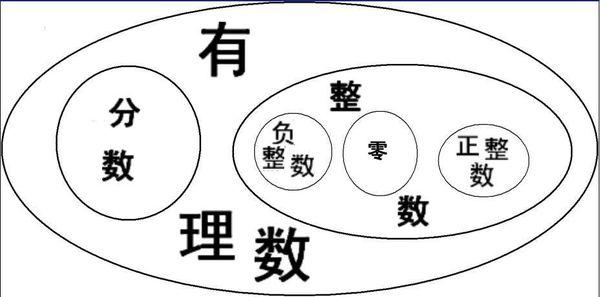 无理数(R-Q) 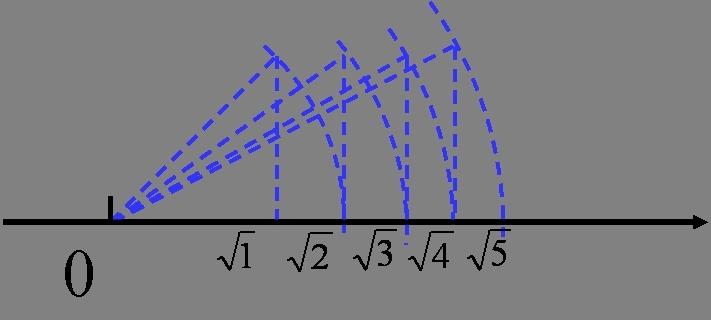 无理数也称为无限不循环小数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。 常见的无理数有非完全平方数的平方根、π和e(其中后两者均为超越数)等。 (责任编辑:admin) |
