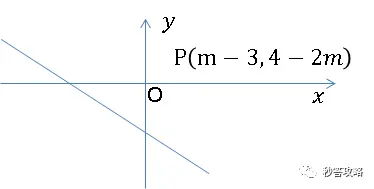|
');
(window.slotbydup=window.slotbydup || []).push({
id: '8096091',
container: s,
size: '580,90',
display: 'inlay-fix'
});
})();
我们今天采用函数图象法秒解一道平面直角坐标系点坐标题目,例题本身比较简单,常规解法也不算太麻烦,因此秒解的意义只有一个,那就是“快!稳!”,题目如下: 无论m为何值,P(m-3,4-2m)不可能在第_________象限。 [常规思路解析] ①若点P在第一象限,则有m-3>0 且 4-2m>0,连立,m无解; ②若点P在第二象限,则有m-3<0 且 4-m>0,连立解得m<3; ③若点P在第三象限,则有m-3<0 且 4-2m<0,连立解得2 ④若点P在第四象限,则有m-3>0 且 4-2m<0,连立解得m>3; ∴无论m为何值,P(m-3,4-2m)不可能在第一象限。 没毛病,根据已知的坐标代数式,按照四个象限分情况讨论,连立解不等式组,即可得到正确答案。这也是我在网上找到的本题的唯一解法。But... ...对于本题,秒答君想说,换个思路,海阔天空,请看秒答解析。 [解析] 1. 由题可知,点P的横、纵坐标均为m的函数,如果我们连立两个函数式,则可以求得点P的纵横坐标之间的关系。 也就是说,设P点坐标为(x,y),由题意,有 x=m-3,y=4-2m,连立消m,可得 y=-2x-2。 2. 可见,无论m为何值,点P都要满足这个关系式。即点P一定在直线 y=-2x-2上, 这是一条斜率为负、截距为负的直线,过二、三、四象限。因此,点P不可能在第一象限。
|