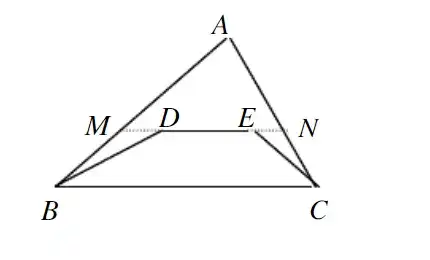
02三角形外角定理证题
    遇到三角形的外角大于任何和它不相邻的内角性质证题时，如果不能直接证明其关系，可以连接两点，或者延长某边与其余两边构成新三角形。
    但是，一定要保证求证的大角在某个三角形的外角位置上，小角在内角的位置上。
    

    辅助线添加后，可以得到新的三角形，再利用三角形的外角定理进行论证。
    这里需要注意的是三角形的外角是等于与它不相邻的两个内角之和的，可以利用这一点进行论证。
    例如下图中的辅助线添加方法：延长BD交AC于E，让∠BDC成为外角。
    

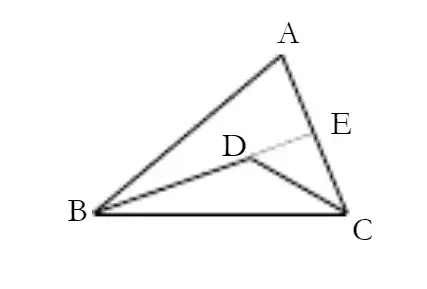
    03全等三角形题
    添加辅助线构建全等三角形一般有三种情况：
    ①题目中有角平分线时，一般会在角的两边截取相等的线段，构建全等三角形。
    ②题目中有以线段中点为端点的线段时，一般会延长该线段，构建全等三角形。
    ③题目中的三角形有中线时，一般会延长中线至两个线段相等，构建全等三角形。
    添加辅助线之后，再利用全等三角形中的相等关系进行解题。
    例如下图中的辅助线添加方法：在DA上截取DN=DB，连接NE和NF，形成两个全等三角形△DBE和△DNE。
    

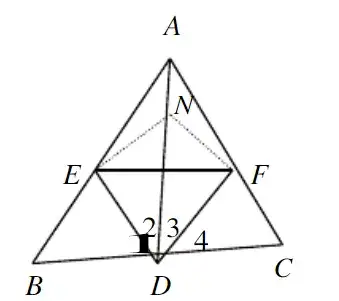
    04三角形截长补短法作辅助线
    如果三角形中的a、b、c、d中的线段有出现以下这三种情况，那么一般就会采取截长补短的方法：
    ① a>b
    ② a±b=c
    ③ a±b=c±d
    截长法就是在较长的线段上截取一段线段，使其和较短线段相等的方法;补短法就是将较短的线段进行延长，使其和较长线段相等的方法。
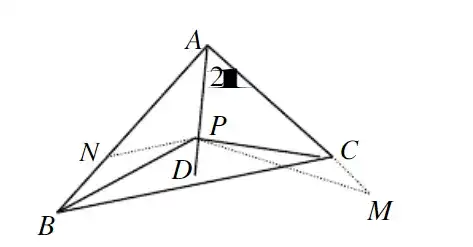
    例如下图中的辅助线添加方法：延长AC至M，使AM=AB，接PM，这样可以形成两个全等三角形：△ABP和△AMP，再运用全等三角形的理论去论证题目。
    

    05延长已知边
    当我们答题时遇到已知条件不足以拿来论证的时候，可以添加辅助线，创建一些新的条件，来为论证服务。
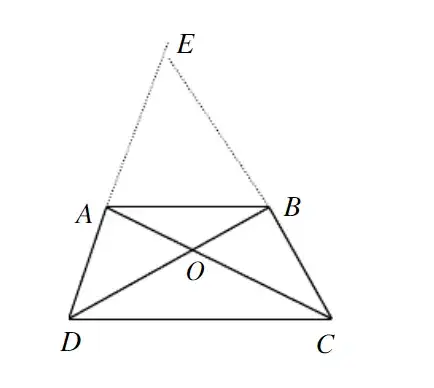
    例如下图中的辅助线添加方法：分别延长DA和CB，交于E点，形成新的三角形。
    

     (责任编辑：admin)