|
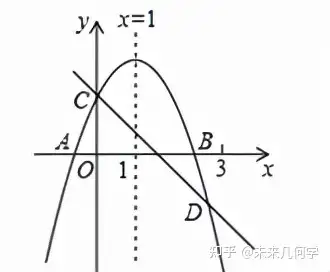
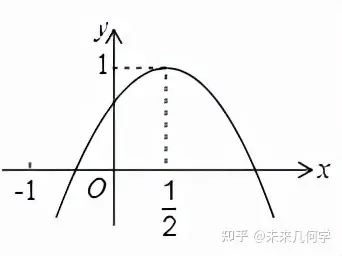
利用二次函数图像判断各系数之间的关系,是中考数学的常考题型,因为综合性较高,题目较难,通常放在选择题或者填空题最后一题,作为小题的压轴题。因此,需要各位同学认真熟悉此种题型的解题方法和技巧。 数学学习 一、基本原理:抛物线与系数之间的关系 已知二次函数y=ax2+bx+c,(a≠0, a、b、c为各项系数) 1、a与抛物线的开口方向及大小之间的关系 抛物线开口向上 a>0, 抛物线开口向下 a<0, |a|越大,抛物线的开口越小 |a|越小,抛物线的开口越大 2、a、b决定抛物线的对称轴 以及 二次函数的最大最小值 1)抛物线对称轴的表达式:x= - b/2a ① b=0时,对称轴为x=0,即y轴; ②当a、b同号时,对称轴<0,即对称轴在y轴左侧; ③当a、b异号时,对称轴>0,即对称轴在y轴右侧; 2)二次函数的最值 ① 当a>0时,二次函数在x= - b/2a处,取最小值(4ac - b²)/4a ② 当a<0时,二次函数在x= - b/2a处,取最大值(4ac - b²)/4a 3、c即抛物线与y轴的交点 因为对于二次函数y=ax2+bx+c,当x=0时,y=c; C>0 、C=0、C<0 ,抛物线与坐标轴分别交于y轴正半轴、原点、y轴负半轴。 4、△ = b²- 4ac 决定抛物线与x轴的交点个数 ① 当△ > 0时,抛物线与x轴有两个交点 ② 当△ = 0时,抛物线与x轴有一个交点 ③ 当△ <0时,抛物线与x轴无交点 二、数形结合:代入特殊值 在确定了抛物线的开口方向、对称轴、最值,以及与坐标轴的交点后,往往只能解决前面一些较为简单的问题。我们还需要依据图形,代入特殊值,才能解决题目中较难的问题。 代入的特殊值一般有x= -1, x= 1, x= -2 ,x=2,x=对称轴 等,以及图形中标出的特殊数值,将这些特殊值代入二次函数解析式中,求出函数值,然后结合图像 (1)与0作比较; (2)与函数最值作比较; (3)如果有一次函数,与一次函数值作比较; (4)或者代入特殊值后,将得到的关于a、b、c表达式进行加减乘除运算等。 下面我们结合例题进行详细讲解: 三、例题解析 例1、如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0; ②a﹣b+c<0; ③x(ax+b)≤a+b; ④a<﹣1.其中正确的是( )
|