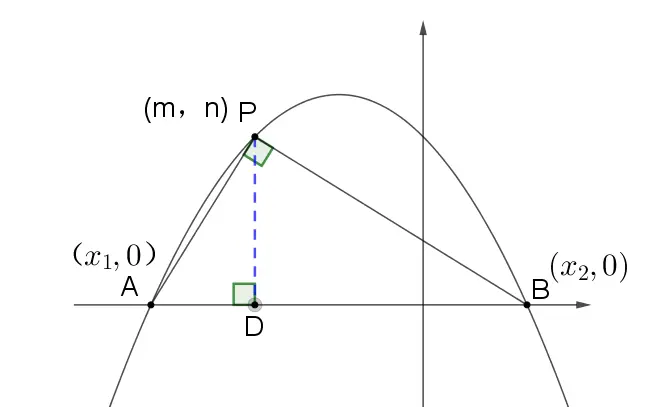
根据射影定理，PD²=AD×DB，可以得n²=(m-x1)(x2-m);
    再结合抛物线两根式，y=a(x-x1)(x-x2)，代入点P坐标，n=a(m-x1)(m-x2)联立之后，即可得出n=-1/a;
    这个结论同学们要掌握好，可以秒杀很多同类的压轴题。
    例题：
    如图，直角三角形ABG的三个顶点均在抛物线y=x²上，并且斜边AB平行于X轴，AG⊥GB，若斜边上的高为h，则( )(视频讲解在文末)
    A. h<1 B. h=1
    C.1
    

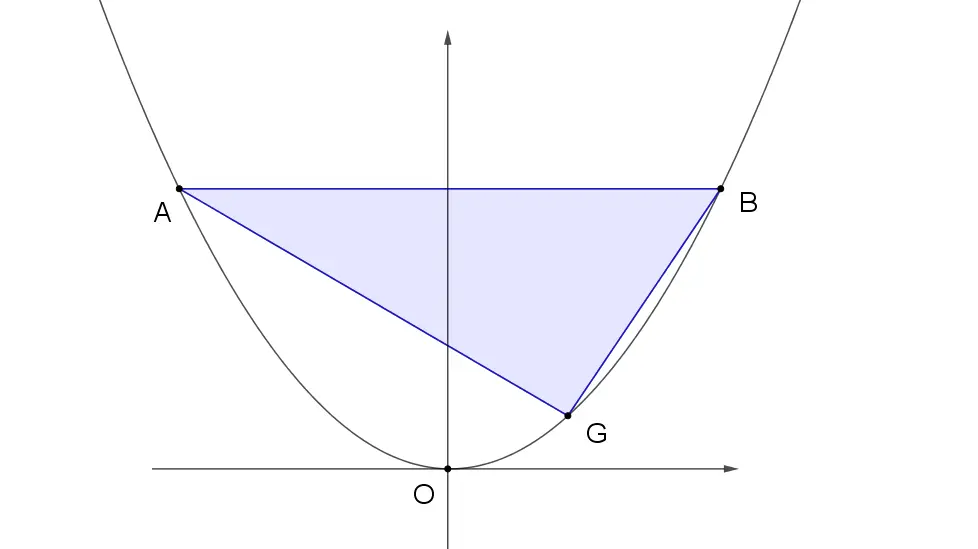
    这个题目让求的是G到AB的距离，我们就可以把函数通过平移符合上面结论的模型来计算。
    假设AB与x轴距离为c，把y=x²向下平移c个单位，得到新的函数y=x²-c，直线AB就相当于x轴了，新函数与x轴的两个交点A、B，点G在抛物线上，且AG⊥GB，求的h不就是点G的纵坐标绝对值吗?
    二次项系数a=1，
    所以h=丨-1/a丨=1
     (责任编辑：admin)