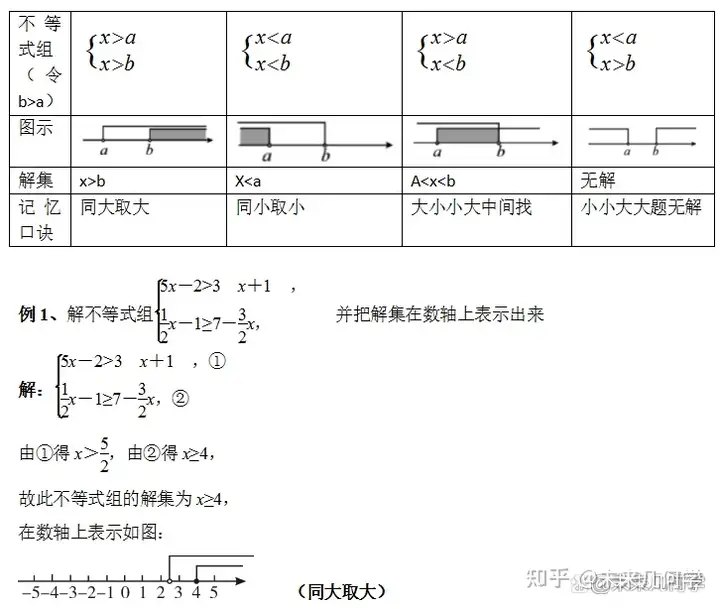
一、解一元一次不等式组的一般步骤:
(1)首先求出各个不等式的解集;
(2)利用数轴确定它们的公共部分;
(3)根据公共部分表示出不等式组的解集。
例2、如图,直线l1的解析式为y=2x-2,直线l1与x轴交于点D,直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求m的值;
(2)求直线l2的解析式;
(3)根据图象,直接写出1

二、求解不等式应用题的一般步骤:
(1)设:合理设未知数
(2)找:根据条件找出已知的或隐含的不等关系
(3)列:列出含有未知数的不等式(组),
(4)解:解不等式(组)
(5)检:最后验证解的合理性并作答(注意此处通常要根据不等式组的解分类讨论)
例4、为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每名老师带队14名学生,则还剩10名学生没老师带;若每名老师带队15名学生,就有1名老师少带6名学生.现有甲、乙两种大型客车,它们的载客量和租金如下表所示:

例5、某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?

(责任编辑:admin) |