|
2005全国课程改革实验区初中毕业学业考试数学学科试题评价报告五 例20 (河北省)图15-1至15-7中的网格图均是20×20的等距网格图(每个小方格的边长均为1个单位长).侦察兵王凯在P点观察区域MNCD内的活动情况.当5个单位长的列车(图中的 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒). ⑴在区域MNCD内,请你针对图15-1,图15-2,图15-3,图15-4中列车位于不同位置的情形分别画出相应的盲区,并在盲区内涂上阴影. ⑵只考虑在区域ABCD内开成的盲区.设在这个区域内的盲区面积是y(平方单位). ①如图15-5,当5≤t≤10时,请你求出用t表示y的函数关系式; ②如图15-6,当10≤t≤15时,请你求出用t表示y的函数关系式; ③如图15-7,当15≤t≤20时,请你求出用t表示y的函数关系式; ④根据①-③中得到的结论,请你简单概括y随t的变化而变化的情况. ⑶根据上述研究过程,请你按不同的时段,就列车行驶过程中在区域MNCD内所形成盲区的面积大小的变化情况提出一个综合的猜想(问题⑶是额外加分题,加分幅度为1-4分). 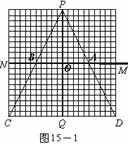 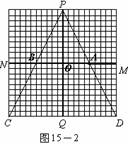  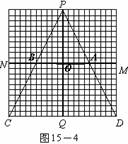  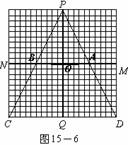 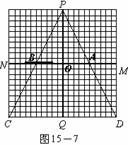 解:(1)相应的盲区如图2~图5所示. (2)①如图6,当 而梯形 ②如图7,当 易知 又  梯形 梯形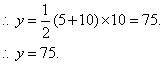 ③如图8,当 且 又  梯形 梯形④当 当 当 (3)通过上述研究可知,列车从 ①在 ②在 ③在 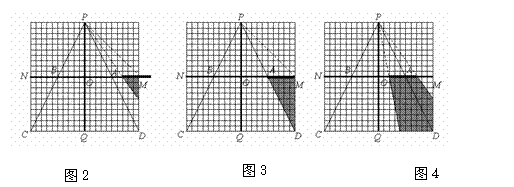 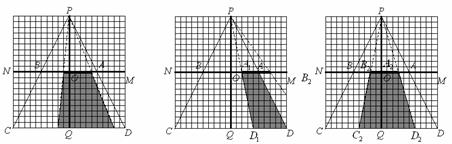 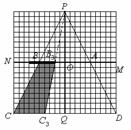 图5 图6 图7 图8 评析 本题是一道压轴题,试题将新课程中视点、视角及盲区的概念放置在侦察兵观察情况这样一个生动的情境中,将几何的面积计算与代数一次函数有机结合在一起,具有较大信息容量和较强的综合性,考查了学生探究能力和综合利用数学知识解决问题的能力,试题难度并不很大.另外第(3)小题是一道“奖优型”的附加题,给数学尖子生一个展示自我的机会,但第(3)小题的要求与第(2)小题第④问的要求似乎有所重复. (责任编辑:admin) |
