|
基于《课程标准》的数学学业考试要点剖析七 四、 关于“数学活动过程”的考查 《课程标准》中有多处明确指出要关注学生的数学学习过程，而不仅仅是数学学习的结果。这一个要求是否可以在数学学业考试中得以体现，一直是广大师生极为关心的事情，事实上，若此目标无法实现，则根据我国的数学教学现状，实践中就很难对此有足够的重视。为此，这一课程目标必将在数学学业考试中有所体现。 具体说来，主要考查学生在数学活动过程中所表现出来的思维方式、思维水平，对活动对象、相关知识与方法的理解深度；从事探究与交流的意识、能力和信心等；能否通过观察、实验、归纳、类比等活动获得数学猜想，并寻求证明猜想的合理性；能否使用恰当的数学语言有条理地表达自己的数学思考过程。通常，这样的考查目标可以通过让学生经历某种形式的数学活动（包括动手操作、思想实验、推理与交流等），以表露自己的思维过程。 例42 下图是由黑点组成的5行5列点阵，任意左右（或上下）相邻的两点间距离是1。  （1） 请以点阵中的点为顶点画面积最小的正方形和面积最大的正方形各一个。 （2） 请再以点阵中的点为顶点画面积次小的正方形和面积次大的正方形各一个。 （3） 若以点阵中的任意点为顶点画正方形，共能画出多少个面积互不相等的正方形？它们的面积分别是多少？ 考查内容：借助“纸笔作图”这种简单的数学活动，考查学生能否在活动中从“无序的试误”走向“有序的操作”，即从开始略带盲目的尝试上升为最终能够把握决定正方形面积大小的核心要素。在这个过程中显然需要进行观察分析、动手验证、归纳总结等多种合情推理活动。 例43 在数学活动课上，老师要求同学们先做下面的“循环分割”操作，然后再探索规律： 如图1，是一等腰梯形纸片，其腰长与上底长相等，且底角分别为60°和120°，按要求开始操作（每次分割，纸片均不得留有剩余）：  第1次分割：先将原等腰梯形纸片分割成3个全等的正三角形，然后将分割出的一个正三角形分割成3个全等的等腰三角形； 第2次分割：先将上次分割出的3个等腰梯形中的一个分割成3个全等的正三角形；然后将刚分割出的一个正三角形分割成3个全等的等腰三角形； 以后按第2次分割的方法进行下去…… （1） 请你在图2中画出第一次分割的方案图。 （2） 若原等腰梯形的面积为a，请你通过操作，观察，将第2次，第3次分割后所得的一个最小等腰梯形面积分别填入下表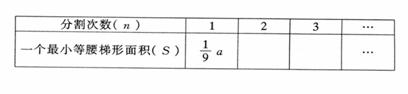：  （3） 请你猜想，分割所得的一个最小等腰梯形面积S与分割次数n有何关系?（请直接用含a的式子表示，不需写推理过程） 考查内容：以“循环分割”的操作活动为问题情境，让学生经历动手操作、观察、思考、归纳、猜想的过程，以考查他在求解问题的过程中中所表现出来的思维水平，对活动对象、相关知识与方法的理解深度；以及从事探究与交流的能力。 例44 还记得完全平方公式：（a+b）2=a2+2ab+b2吗？当a,b>0时，完全平方公式可以用下图1来说明. 对下图2进行适当的分割，猜想出（a+b+c）2的展开形式，并给出其推导过程。  图1 图2 考查内容：对完全平方公式推导过程以及几何图示的理解水平；在理解的基础上进行方法的迁移运用，从而获得有关猜想，并对猜想进行适当的推导证明的活动能力。 例45 图3是一个经过改造的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球可以经过多反射），那么该球最后将落入的球袋是 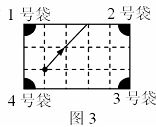 A．1 号袋 B．2 号袋 C．3 号袋 D．4 号袋 评析：本题需要学生经历一定的实验操作过程（也可以将纸上的操作活动转化为脑中的思维活动）获得问题的最终解决，因而，本题通过结果的选择考查了学生的数学活动过程。 例46 扑克牌游戏：小明背对小亮，让小亮按下列四个步骤操作： 第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌现有的张数相同； 第二步 从左边一堆拿出两张，放入中间一堆； 第三步 从右边一堆拿出一张，放入中间一堆； 第四步 左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 . 考查内容：考查了整式的加减问题，展示了用数或式来表达和交流信息，从而为解决问题而选择适当的算法的过程，也关注了对“探索具体问题中的数量关系和变化规律”目标的考查。 最后，出于对新课程关注学生个性评价这一理念的贯彻，数学学业考试中还将突出对学生思维“个性化”做出评价的思路。 具体的方式包括： ● 设置自主选择试题──在试卷上设立可以选做的试题，让学生根据自己的数学学习状况、认知特征，选择恰当的试题做答，以充分表现自己数学学习才能； ● 提供开放性试题──在试卷上设立了开放性试题，力图使得每一个学生都能够根据自己的思考角度、对试题背景的理解程度，提出一个问题、给出一个结论（猜想）、或提供一种结论之所以成立的解释（证明），等等； ● 制订个性化评分标准──对于某些具有个性化的试题求解过程，例如提出问题、给出开放性试题的答案等，制订一个开放的、不同类型、不同层次的评分标准，使得所有对试题提供了实质性解答的学生都能够获得相应的分数，而不是简单地将学生的解答套入事先预定的“标准解答”体系之中。 例47 已知抛物线 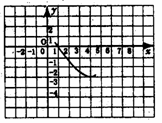 的部分图象（如图），图象再次与x轴相交时，交点的坐标是（ ） （A）（5，0） （B）（6，0） （C）（7，0） （D）（8，0） 点评：本题所考查的对象是有关函数的一个基本特性。试题采用数形结合的方法给出部分信息，既给擅长不同思维方式的学生提供了不同的思路，又有效地考查了相关的重要内容。学生可以利用函数与方程的关联通过解一元二次方程  求出图象与x轴的另一交点坐标，也可以利用抛物线的几何性质的学生也可利用抛物线的轴对称性来确定另一点的坐标，两种方法都是数学中的重要内容。例48 如图，在20×20的等距网络（每格的宽和高均是1个单位长）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动，设运动时间为x秒，△QAC的面积为y 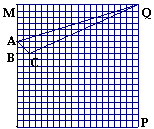 （1） 如图，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中 画出Rt△A1B1C1关于直线QN成轴对称的图形； （2） 在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？ （3）在Rt△ABC向右平移的过程中，请你说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？为什么？ （说明：在（3）中，将视你解答方法的创新程度，给予1—4分的加分） 点评：本题以一个动态的几何变化过程及其相应的面积函数为背景，有利于让具有不同认知风格的学生从不同角度看待变化过程，不同水平的学生都能以自己的方式理解题意，从事探索性数学活动。 例49（本题有3小题，第（1）小题为必答题，满分5分；第（2）、（3）小题为选答题，其中第（2）小题满分3分，第（3）小题满分6分，请从中任选1小题作答，如两题都答，以第（2）小题评分.） 在△ABC中，∠ACB = 90，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E. 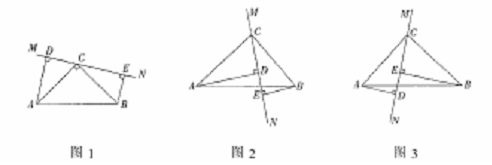 （1）当直线MN绕点C旋转到图1的位置时，求证： ① △ADC≌△CEB； ② DE=AD+BE； （2）当直线MN绕点C旋转到图2的位置时，求证：DE = AD-BE； （3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明. 注意：第（2）、（3）小题你选答的是第 小题. 点评：本题通过直线的MN的旋转构造问题，蕴含了对观察、动手操作、猜测、合理推断、合理推理论证等数学活动的考查。试题的要求层次分明──其区别的实质在于对题中蕴涵的“对称”现象的领悟，使学习水平层次不同的学生在考试中有发挥的机会和余地，本题的第（2）、（3）小题可任选一题，这样既能尊重学生的数学差异、能保障不同层次的学生得到不同的评价，又有利于激发学生的思维激情和潜能。 (责任编辑：admin) |