|
突出课标理念、寻求有价值的试题难度 ──2010年遵义市中考试题27题解读 贵州省道真县玉溪镇中心学校 胡 军 题目：如图，已知抛物线  的顶点坐标为Q ，且与 轴交于点C ，与 轴交于A、B两点（点A在点B的右侧），点P是该抛物线上一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥ 轴，交AC于点D． (1)求该抛物线的函数关系式； (2)当△ADP是直角三角形时，求点P的坐标； (3)在问题(2)的结论下，若点E在 轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．一、试题特点分析： 1.试题的综合性设置： 此题以平面直角坐标系为载体，综合考查了一次函数、二次函数、一元一次方程、一元二次方程、二元一次方程组、二次根式、轴对称、三角形与四边形等初中数学的主干知识；在能力上考查了学生对数学知识的分析、观察与计算、灵活运用数学知识的能力；在思想方法上考查了转化思想、分类讨论思想、数学建模思想、函数思想、数形结合思想等。本题将二次函数、二次方程、特殊四边形及对称性等知识综合于一题，在知识的交汇处做文章，达到了考查学生综合解决问题的能力。是一道综合性较强的题目。 2.试题的难度考查： 试题共设置了3道小题。第（1）小题为基础题，即已知项点坐标和抛物线上一点求解析式。考查了二次函数的解析式、一元一次方程等知识，多数学生能正确解答，是解决第（2）小题的基础. 第（2）问给出△ADP是直角三角形这一条件，求P点坐标，需要分两种情况进行讨论，①是点P为△APD直角顶点，②是点A为△APD的直角顶点，考查学生在动态背景下几何关系的认识能力与函数知识的应用能力，动中有静，静中有动，变与不变相互转换为后面作好铺垫。考查了一元二次方程，等腰直角三角形的三线合一，轴对称、一次函数、二元一次方程组，一元二次方程，二次函数的有关知识。有一定的难度。第（3）问化动为静，在（2）问确定P点位置后，探究存在以A、P、E、F为顶点的平行四边形的可能性，此问新颖地将平行四边形的考查与平面直角坐标系、二次方程等代数学知识的考查有机地结合在了一起。对F点的存在性讨论，既要考虑对P点两种不同位置进行分类判析，又要利用F点既是抛物线上点又是平行四边形顶点这两个条件，对问题进行建模，提升了对数学本质的思考，综合考查了平移、平行四边形、一元二次方程等初中阶段主要的核心知识和数学思想，学生的运算能力及运用所学知识分析问题的能力也得以充分考查，为筛选优秀学生提供了很好的素材。属于中上难度的问题和能力考查的范围。 3.试题的背景选择： 试题以平面直角坐标为载体，渗透运动变化的背景，“点P是该抛物线上一动点，从点C沿抛物线向点A运动 ……”。运动变化使题目的各种关系变得复杂，学生要用运动的观点来分析图形在运动过程中的相互关系，从而考查学生的思维能力。 4.试题的条件隐蔽 此题作为压轴题，对命题有较高要求。对学生的数学思维能力同样要求高，学生要正确解出此题，有三道坎：一是求该抛物线的函数关系式；此坎多数学生能迈过；二是当△ADP是直角三角形时，求点P的坐标，要用分类讨论；学生在解题过程中往往会丢掉第二种情况，即：点A为△APD的直角顶点。如果没有考虑到这一种情况，就会失去对此题完整解答的机会。三是探究“是否存在以A、P、E、F为顶点的平行四边形”？要求学生具有较强的观察力与分析力。在试题中，有的条件是明了的，有的则是隐蔽的。如第（2）问中要分P、A为直角三角形的顶点进行讨论。 二、试题的解法 解法一：（1）∵抛物线的顶点为Q（2，-1）,∴设  ，将C（0，3）代入上式解得  ， ∴  ， 即 ,⑵分两种情况： ①当点P1为直角顶点时,点P1与点B重合(如图)  令 =0, 得 解之得 ,  ，∵点A在点B的右边, ∴B(1,0), A(3,0)，∴P1(1,0). ②当点A为△APD2的直角顶点是(如图)  ∵OA=OC, ∠AOC=  , ∴∠OAD2= ,当∠D2AP2=时, ∠OAP2=,∴AO平分∠D2AP2又∵P2D2∥轴, ∴P2D2⊥AO, ∴P2、D2关于 轴对称.设直线AC的函数关系式为 ,将A(3,0), C(0,3)代入上式得  , ∴ ∴  ,∵D2在 上, P2在上,∴设D2( , ), P2(, )∴( )+()=0, , ∴ , (舍), ∴当 =2时, = =-1,∴P2的坐标为P2(2,-1)(即为抛物线顶点) ∴P点坐标为P1(1,0), P2(2,-1). (3)由题(2)知,当点P的坐标为P1(1,0)时,不能构成平行四边形； 当点P的坐标为P2(2,-1)(即顶点Q)时,平移直线AP(如图)交 轴于点E,交抛物线于点F.当AP=FE时,四边形PAFE是平行四边形.∵P(2,-1), ∴可令F( ,1)，∴  解之得:  ,  ∴F点有两点,即F1(  ,1), F2( ,1)下面我们再研究第二问的不同解法。 解法二：①显然，当P与点B重合时P的坐标为P1（2，-1）；  ②又AB=2，∠OAD2=  ,Q(2，-1)，作QH⊥AB于H，∴QH=1，QH=1/2AB=AH=1,∴∠QAD=  ,∴当点P与点Q重合时△PAD是直角三角形，∴P的坐标为P2（2，-1） 解法三：①显然，当P与点B重合时P的坐标为P1（2，-1）； ②连接CQ、AQ，可得  , ∵  ,∴∠CAQ=,(勾股定理逆定理)，即当点P移动到点Q（顶点）时，有∠CAP(Q)= ,∴△PAD是直角三角形，∴P的坐标为P2（2，-1） 解法四：①显然，当P与点B重合时P的坐标为P1（2，-1）； ②若∠DAP= ，设DP与OA交于点H，∵∠OAD=，∴∠OAP=,设AH=HP=x，∴OH=3-x，则P（3-x,-x）,点P在抛物线  上，∴有  ，解之得 当  时，P（3，0），与点A重合（舍）；当  时，P2（2，-1），与Q重合.解法五：①显然，当P与点B重合时 P的坐标为P1（2，-1）； ②过点A作AP⊥CA，交抛物线于点P， 作 PD∥ 轴,交OA于H，设HB= ,AH= ,显然，DH=AH=PH=  ，OH= ，∴P（  ， ），将点P坐标代入，得 ，解之得， 当  时，P2（2，-1）与Q重合；当  时，P（3，0）与A重合（舍） 解法六：（利用相似求解） 直线AC:  , D(x,-x+3),DP=-x+3-(x2-4x+3)=-x2+3x,延长DP交OA于点E，∵A（3,0），E（x,0）∴AE=DE=OA-OE=3-x,AD=  ,①当∠DPA=∠COA= 时，∵PD∥轴,∴△PAD∽△COA,  即  ，解之得 ∴P（1，0）与B重合，P（3，0）与A重合（舍） ②当∠DAP=∠COA= 时, △PAD∽△COA, ,即  ，解之得， ，∴P（2，-1）与Q点(顶点)重合，∴P1（1，0），P2（2，-1）.三、同类试题展示 1.（2010年毕节）如图，在平面直角坐标系中，抛物线y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2，0)、B(4，0)，与y轴交于点C(0，4)，直线l是抛物线的对称轴，与x轴交于 点D，点P是直线l上一动点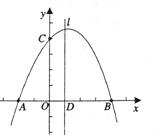．  (1)求此抛物线的表达式； (2)当AP+CP的值最小时，求点P的坐标；再以点A为圆心，AP的长为半径作⊙ A求证BP与⊙A相切； (3)点P在直线l上运动时是否存在等腰△ACP?若存在，请写出所有符合条件的点P坐标；若不存在，请说明理由． 2.如图，（2010年甘肃定西）抛物线与x轴交于A（－1，0）、B（3，0）两点，与y轴交于点C（0，－3），设抛物线的顶点为D． ⑴求该抛物线的解析式与顶点D的坐标； ⑵以B、C、D为顶点的三角形是直角三角形吗？为什么？ ⑶探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请指出符合条件的点P的位置，并直接写出点P的坐标；若不存在，请说明理由． 3.（2010年河南）在平面直角坐标系中，已知抛物线经过A 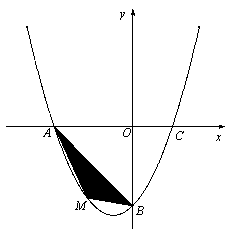 ，B ，C 三点． ⑴求抛物线的解析式； ⑵若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值． ⑶若点P是抛物线上的动点，点Q是直线  上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．4.已知：（2010年荆门）如图一次函数y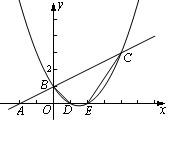＝  x＋1的图象与x轴交于点A，与y轴交于点B；二次函数y＝x2＋bx＋c的图象与一次函数y＝x＋1的图象交于B、C两点，与x轴交于D、E两点且D点坐标为(1，0) (1)求二次函数的解析式； (2)求四边形BDEC的面积S； (3)在x轴上是否存在点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由． (责任编辑：admin) |