聚焦中考阅读理解题
江苏省东台市实验中学教育集团 周礼寅
试题首先提供一定的材料,或介绍一个概念,或给出一种解法等,让你在理解材料的基础上,获得探索解决问题的方法,从而加以运用,解决实际问题,这类问题就是数学的阅读理解题.通过这类问题考查阅读理解、分析转化、范例运用、探索归纳等多方面的素质和能力.
解答阅读理解问题首先应仔细阅读信息,弄清信息所提供的数量关系,然后将信息转化为数学问题,就其本质进行归纳加工、猜想、类比和联想,作出合情判断和推理.
一、新知识型阅读理解题
命题者给定一个陌生的定义或公式或方法,并要求解决新问题,这类考题能考查自学能力和阅读理解能力,接收、加工和利用信息的能力.
例1 (2010年辽宁沈阳)阅读下列材料,并解决后面的问题:
阅读材料:
(1) 等高线概念:在地图上,我们把地面上海拔高度相同的点连成的闭合曲线叫等高线.例如,如图1,把海拔高度是50米、100米、150米的点分别连接起来,就分别形成50米、100米、150米三条等高线.
(2) 利用等高线地形图求坡度的步骤如下:(如图2)
步骤一:根据两点A、B所在的等高线地形图,分别读出点A、B的高度;A、B两点的铅直距离=点A、B的高度差;
步骤二:量出AB在等高线地形图上的距离为d个单位,若等高线地形图的比例尺为1:n,则A、B两点的水平距离=dn;
步骤三:AB的坡度= ; ;

请按照下列求解过程完成填空,并把所得结果直接写在答题卡上.
某中学学生小明和小丁生活在山城,如图3(示意图),小明每天上学从家A经过B沿着公路AB、BP到学校P,小丁每天上学从家C沿着公路CP到学校P.该山城等高线地形图的比例尺为1:50000,在等高线地形图上量得AB=1.8厘米,BP=3.6厘米,CP=4.2厘米.
(1) 分别求出AB、BP、CP的坡度(同一段路中间坡度的微小变化忽略不计);
(2) 若他们早晨7点同时步行从家出发,中途不停留,谁先到学校?(假设当坡度在 到 到 之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在 之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在 到 到 之间时,小明和小丁步行的平均速度均约为1米/秒) 之间时,小明和小丁步行的平均速度均约为1米/秒)
解:(1) AB的水平距离=1.8?50000=90000(厘米)=900(米),AB的坡度= = = ; ;
BP的水平距离=3.6?50000=180000(厘米)=1800(米),BP的坡度= = = ; ;
CP的水平距离=4.2?50000=210000(厘米)=2100(米),CP的坡度= j ;
(2) 因为 < < < < ,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒. ,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒.
因为 k ,所以小丁在路段CP上步行的平均速度约为 l 米/秒,斜坡AB的距离= ?906(米),斜坡BP的距离= ?906(米),斜坡BP的距离= ?1811(米),斜坡CP的距离= ?1811(米),斜坡CP的距离= ?2121(米),所以小明从家到学校的时间= ?2121(米),所以小明从家到学校的时间= =2090(秒) .小丁从家到学校的时间约为 m 秒.因此, n 先到学校. =2090(秒) .小丁从家到学校的时间约为 m 秒.因此, n 先到学校.
分析:对于(1),CP的坡度= ,对于(2),因为 ,对于(2),因为 ,所以小丁在路段CP上步行的平均速度约为1米/秒,小丁从家到学校的距离= ,所以小丁在路段CP上步行的平均速度约为1米/秒,小丁从家到学校的距离= (米),因此所用时间为2121秒. (米),因此所用时间为2121秒.
答案:① ,② ,② ,③1,④2121, ⑤小明 ,③1,④2121, ⑤小明
评注:本题以填空题的形式巧妙利用地理中的等高线设置问题情境,考查了阅读理解能力.用数学知识解决跨学科问题,也是中考数学命题的一种趋势.
例2 (2010年江苏镇江)
深化理解
对非负实数x“四舍五入”到个位的值记为<x>,即:
当n为非负整数时,如果 则<x>=n 则<x>=n
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①<π>= (π为圆周率);
②如果<2x-1>=3,则实数x的取值范围为 ;
(2)①当 ; ;
②举例说明 不恒成立; 不恒成立;
(3)求满足 的所有非负实数x的值; 的所有非负实数x的值;
(4)设n为常数,且为正整数,函数y=x2-x+ 的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足 的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足 的所有整数k的个数记为b. 求证:a=b=2n. 的所有整数k的个数记为b. 求证:a=b=2n.
分析:(1)<π>=3;根据定义得3- ≤2x-1<3+ ≤2x-1<3+ ,可解得x的取值范围;(2)①分别表示出<x+m>和<x>,即可得到所求不等式;②举出反例说明即可,如稍超过0.5的两个数相加;(3) ,可解得x的取值范围;(2)①分别表示出<x+m>和<x>,即可得到所求不等式;②举出反例说明即可,如稍超过0.5的两个数相加;(3) 为整数,设这个整数为k,易得这个整数应在应在k- 为整数,设这个整数为k,易得这个整数应在应在k- 和k+ 和k+ 之间,包括k- 之间,包括k- ,不包括k+ ,不包括k+ ,求得整数k的值即可求得x的非负实数值;(4)易得二次函数的对称轴,可求得二次函数的函数值在相应的自变量的范围内取值,进而求得相应的a的个数;利用所给关系式易得 ,求得整数k的值即可求得x的非负实数值;(4)易得二次函数的对称轴,可求得二次函数的函数值在相应的自变量的范围内取值,进而求得相应的a的个数;利用所给关系式易得 的整数个数为2n,由此得证. 的整数个数为2n,由此得证.
答案:(1)①3;② ;(2)①证明:设<x>=n,则n- ;(2)①证明:设<x>=n,则n- ≤x<n+ ≤x<n+ ,n为非负整数;又(n+m)- ,n为非负整数;又(n+m)- ≤x+m<(n+m)+ ≤x+m<(n+m)+ ,且m+n为非负整数, ,且m+n为非负整数,
∴<x+m>=n+m=m+<x>
②举反例:<0.6>+<0.7>=1+1=2,而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>,∴<x>+<y>= <x+y>不一定成立.
(3)∵x≥0,  为整数,设 为整数,设 =k,k为整数 =k,k为整数
则x= ,∴< ,∴< >=k,∴ >=k,∴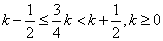
∵0≤k≤2,∴k=0,1,2 ∴x=0,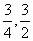
(4)∵函数y=x2-x+ =(x- =(x- )2,n为整数, )2,n为整数,
当n≤x<n+1时,y随x的增大而增大,
∴(n- )2≤y<(n+1- )2≤y<(n+1- )2即(n- )2即(n- )2≤y<(n+ )2≤y<(n+ )2, ① )2, ①
∴n2-n+ ≤y<n2 +n+ ≤y<n2 +n+ ,∵y为整数 ,∵y为整数
∴y= n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y.
∴a =2n ② (8分)
则 ③ ③
比较①,②,③得:a=b=2n
评注:这是一道创新题,要求读懂定义,能用定义解决简单的实际问题,然后能更进一步地结合已经学过的知识进行拓展,是一道不易的压轴题,要在短时间解决此问题,要求平时的学习要有一定的创新思维,特别是自学习能力的培养显得尤为重要.就这题而言,对不等式组,及不等式组的整数解的应用要掌握得非常熟练,对二次函数式的变形能力要求也较高.
二、新方法型阅读理解题
在已有知识的基础上,设计一个陌生的数学情景,通过阅读相关信息,引入新方法进行猜想解答的一类新题型.解题关键是理解材料中所提供的解题途径和方法,运用归纳与类比的方法去探索新的解题方法.
例3(2010广东东莞)阅读下列材料:
1×2= (1×2×3-0×1×2), (1×2×3-0×1×2),
2×3= (2×3×4-1×2×3), (2×3×4-1×2×3),
3×4= (3×4×5-2×3×4), (3×4×5-2×3×4),
由以上三个等式相加,可得
1×2+2×3+3×4= ×3×4×5=20. ×3×4×5=20.
读完以上材料,请你计算下各题:
⑴1×2+2×3+3×4+…+10×11(写出过程);
⑵1×2+2×3+3×4+…+n×(n+1)= ;
⑶1×2×3+2×3×4+3×4×5+…+7×8×9= .
分析: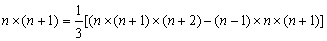
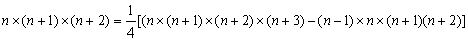
答案:⑴1×2+2×3+3×4+…+10×11
= ×(1×2×3-0×1×2+…+10×11×12-9×10×11) ×(1×2×3-0×1×2+…+10×11×12-9×10×11)
= ×10×11×12 ×10×11×12
=440
⑵1×2+2×3+3×4+…+n×(n+1)
= ×[1×2×3-0×1×2+…+ ×[1×2×3-0×1×2+…+ ] ]
=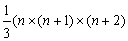
⑶1×2×3+2×3×4+3×4×5+…+7×8×9
= ×[1×2×3×4-0×1×2×3×4+…+7×8×9×10-6×7×8×9] ×[1×2×3×4-0×1×2×3×4+…+7×8×9×10-6×7×8×9]
= ×7×8×9×10 ×7×8×9×10
=1260
评注:本题通过材料来探索有规律的数列求和公式,并应用此公式进行相关计算.本题系初、高中知识衔接的过渡题,对考查探究学习、创新能力及综合运用知识的能力都有较高的要求.这些数列的求和公式的探索,需要认真阅读材料,寻找材料中提供的解题方法与技巧,第(3)问是在第(2)问的基础上通过类比得到的.
例4(2010年北京)阅读下列材料:
小贝遇到一个有趣的问题:在矩形ABCD中,AD=8cm,AB=6cm.现有一动点P按下列方式在矩形内运动:它从A点出发,沿着AB边夹角为45°的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45°的方向作直线运动,并且它一直按照这种方式不停地运动,即当P点碰到BC边,沿着BC边夹角为45°的方向作直线运动,当P点碰到CD边,再沿着与CD边夹角为45°的方向作直线运动,…,如图4所示,问P点第一次与D点重合前与边相碰几次,P点第一次与D点重合时所经过的路线的总长是多少.小贝的思考是这样开始的:如图5,将矩形ABCD沿直线CD折迭,得到矩形A1B1CD,由轴对称的知识,发现P2P3=P2E,P1A=P1E.
请你参考小贝的思路解决下列问题:
(1) P点第一次与D点重合前与边相碰 次;P点从A点出发到第一次与D点重合时所经过的路径的总长是 cm;
(2) 近一步探究:改变矩形ABCD中AD、AB的长,且满足AD>AB,动点P从A点出发, 按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上.若P点第一次与B点重合前与边相碰7次,则AB:AD的值为 .
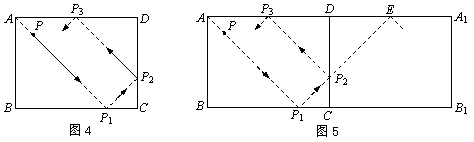 
分析:(1)画出如图6所示的草图分析易知,相碰5次(P1~P5),路径的总长均是等腰直角三角形的斜边长之和;(2)解题思路如图7:
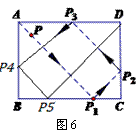 
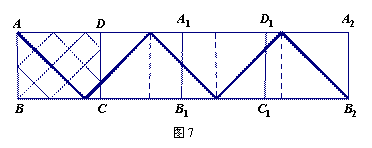 
答案:(1)5,24;(2)4∶5.
评注:这是2010年一道亮点试题,有效考查了对称变换、转化思想.作为一道阅读理解试题,小贝提供的解法思路对于问题的获解有很好启示,需要认真解读、理解.这也是“方法”阅读问题的解答关键.
三、新技巧型阅读理解题
例5 (2010年湖南永州)探究问题
(1)阅读理解:
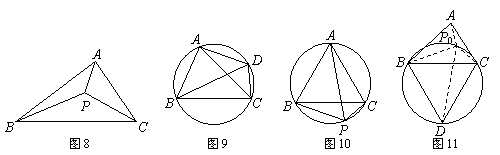
①如图8,在△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
②如图9,若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+BC·AD=AC·BD.此为托勒密定理.
(2)知识迁移:
①请你利用托勒密定理,解决如下问题:
如图10,已知点P为等边△ABC外接圆的上任意一点.求证:PB+PC=PA.
②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120?)的费马点和费马距离的方法:
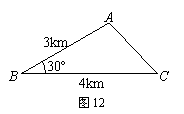
第一步:如图11,在△ABC的外部以BC为边长作等边△BCD及其外接圆;
第二步:在上取一点P0,连接P0A、P0B、P0C、P0D.
易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+ ;
第三步:请你根据(1)①中定义,在图11中找出△ABC的费马点P,线段 的长度即为△ABC的费马距离.
(3)知识应用:
2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难.为解决老百姓饮水问题,解放军某部到云南某地打井取水.已知三村庄A、B、C构成了如图12所示的△ABC(其中∠A、∠B、∠C均小于120?),现选取一点P打水井,使水井P到三村庄A、B、C所铺设的输水管总长度最小.求输水管总长度的最小值.
分析:(2)第①问,只需按照题意套用托勒密定理,再利用等边三角形三边相等,将所得等式两边都除以等边三角形的边长,即可获证. 第②问,借用①问结论,及“两点之间线段最短” 的性质容易获解.(3)在(2)的基础上先画出图形,再求解.
答案:(2)①证明:由托勒密定理可知PB·AC+PC·AB=PA·BC
∵△ABC是等边三角形
∴ AB=AC=BC
∴PB+PC=PA
②P′D AD
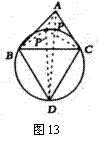 
(3)解:如图,以BC为边长在△ABC的外部作等边△BCD,连接AD,则知线段AD的长即为△ABC的费马距离.
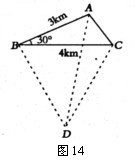 
∵△BCD为等边三角形,BC=4,
∴∠CBD=60°,BD=BC=4.
∵∠ABC=30°, ∴∠ABD=90°.
在Rt△ABD中,∵AB=3,BD=4
∴AD= = = =5(km) =5(km)
∴从水井P到三村庄A、B、C所铺设的输水管总长度的最小值为5km.。
评注:此题集阅读理解、创新探究、实际应用于一体,题型新颖别致,综合考查自主探究、创新应用能力,是一道不可多得的好题. 此题环环相扣,解题关键是理解阅读材料,从中获取新知,能够灵活应用新知解决数学问题,并进一步构建数学模型解决实际问题. 此题难度中等,只要平时养成自主学习的习惯,并善于将所学知识融会贯通,便可顺利解决问题.
(责任编辑:admin) |















