|
中考最值问题探究 江西省安福县城关中学 曹经富 中考压轴题中频繁出现有关最值问题，常让很多同学束手无策，望而生畏，其实解这类试题关键是要结合题意，借助相关的概念、图形的性质，将最值问题化归与转化为相应的数学模型（函数增减性、线段公理、三角形三边关系等）进行分析与突破，现结合近年各地试题的特点进行剖析，希望能给同学一定的启示与帮助。 一、在线段之和的最值问题中酝酿与构建，借用线段公理求解 例1（湖北荆门）如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为( )  A 2  B C 1 D 2解析：PA+PB的线段之和最小值求法的依据是“平面几何中，两点之间线段最短”的数学模型与原理，故可作B 关于MN的对称点是H，连接AH交MN于点P，AH的长就是PA+PB的线段之和的最小值，借助圆圆周角定理，可知根据∠AOH＝90°，巧妙构造Rt△OAH，根据题意运用勾股定理可求出AH=  ，所以PA+PB的最小值为故选B。点评：本题是课本著名原题“泵站问题”的变形与应用，解决本题的关键做出点B或A关于MN的对称点，然后利用线段垂直平分线的性质和两点之间线段最短,并借助圆心角和圆周角的关系，构造直角三角形运用勾股定理计算最小值来解决问题．不管在什么背景图中，有关线段之和的最短问题，常化归与转化为线段公理“两点之间，线段最短”。而化归与转化的方法大都是借助于“轴对称点”。 例2 圆锥底面半径为10cm，高为10 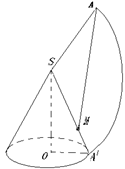 cm， （1） 求圆锥的表面积； （2） 若一只蚂蚁从底面一点A出发绕圆锥一周回到SA上一点M处，且SM=3AM，求它所走的最短距离。 思路点拨：利用底面半径、高及母线组成的直角三角形构造勾股定理求出母线长，进而借助扇形面积公式求出表面积；蚂蚁在圆锥表面上行走一圈，而圆锥侧面展开后为扇形，故可在展开图（扇形）上求点A到M的最短距离（即AM的长）。 解析：（1）圆锥的母线长SA=  ，圆锥侧面展开图扇形的弧长 ， 侧  ，S底= ，∴S表= S底+ S侧=  。（2）沿母线SA将圆锥的侧面展开，得圆锥的侧面展开图，则线段AM的长就是蚂蚁所走的最短距离，由（1）知  ，弧AA′=  ， ，又SA′= AS= ，SM=3A′M，∴SM= ，∴在Rt⊿ASM中，  ，所以蚂蚁所走的最短距离是50cm.点评：对于立体图形中要计算圆锥曲面上两点之间的最短距离，一般把立体的圆锥的侧面展开成扇形，转化为平面图形借助线段公理计算。将立体图形转化为平面图形是初中阶段常用的基本方法与思想。 二、在具体情境中最值问题，借用函数图象的增减性求解 例3（山东济南）如图，已知抛物线 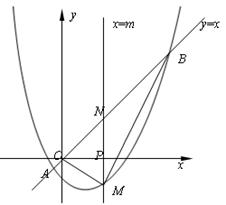 经过点（1，-5）和（-2，4） （1）求这条抛物线的解析式． （2）设此抛物线与直线y=x相交于点A，B（点B在点A的右侧），平行于  轴的直线 与抛物线交于点M，与直线 交于点N，交 轴于点P，求线段MN的长（用含 的代数式表示）．（3）在条件（2）的情况下，连接OM、BM，是否存在 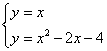的值，使△BOM的面积S最大？若存在，请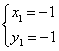求出的值，若不存在，请说明理由．解析：（1）由题意得  ，解得b=—2，c=—4，故抛物线解析式为y=x2—2x—4（2）由题意得  ，解得 ， ，∴B点坐标为（4，4）将x=m代入y=x得y=m，点N的坐标为（m，m），同理点M的坐标为（m，m2—2m—4）∴MN= m－（m2—2m—4）＝—m2+3m+4 （3）作BC⊥MN于点C，则BC=4—m，OP=m，S=  MN·OP+MN·BC=2（—m2+3m+4）=—2（m— ）2+ ，∵—2＜0，∴当m=时，S有最大值点评：由具体情境酝酿与构建最值问题，通常有两种形式，一是在商品经营活动中，经常会遇到求最大利润、最大销量等问题，解此类问题的关键是通过题意及现实数量关系，确定出相关函数的表达式，另一类是在几何图形中有关面积的最值问题，解这类问题关键是要掌握图形面积的求解与表示，构建相应的函数关系式，进而根据函数图象的增减性确定其最值，并注意问题的实际意义。本题涉及两函数间的距离计算，距离可能是平行于x轴的AB两点间的距离：ABx=︳Ax-Bx︱；也可能是平行于y轴的AB两点间的距离：ABy=︳Ay-By︱,在本题中还可进一步设问，求线段MN长度的最大值，这种问题在近几年各地中考中频繁出现，解这类题往往是通过用变量表示MN的长度，进而构建相应的函数模型，借助函数图象的增减性进行求解最值。 三 在线段之差的最值问题，借用三角形三边关系求解。 例4：（贺州）如图，抛物线 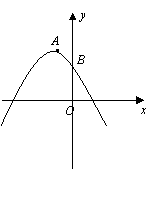 的顶点为A，与y 轴交于点B． （1）求点A、点B的坐标． （2）若点P是x轴上任意一点，求证：  ．（3）当  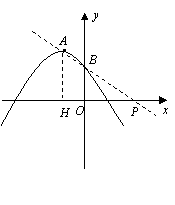最大时，求点P的坐标． 解析：（1）抛物线  与y轴的交于点B，令x=0得y=2．∴B（0，2）， ∵  ，∴A（—2，3） （2）当点P是 AB的延长线与x轴交点时，  ． 当点P在x轴上又异于AB的延长线与x轴的交点时， 在点P、A、B构成的三角形中，  ．综合上述： （3）作直线AB交x轴于点P，由（2）可知：当PA—PB最大时，点P是所求的点 作AH⊥OP于H．∵BO⊥OP，∴△BOP∽△AHP，∴  由（1）可知：AH=3、OH=2、OB=2，∴OP=4，故P（4，0） 点评：点P为任意一点时，要探究PA－PB的最大值，可数形结合，将其转化为相关图形（三角形），三边关系始终满足两边之差小于第三边（︳PA－PB︱<AB），而当点A、B、P在同一直线上时存在PA－PB＝AB，此时AB为最大值，今后有关两线段之差的最大值问题，常借助“三角形两边之差小于第三边”，将其最大值转化为一条特殊（三点共线）线段的长。 作者简介：曹经富，男，中学高级教师，数学教研组长，立足课堂教学，潜心钻研中考及解题研究，发表文章百余篇，主编书稿4本。 (责任编辑：admin) |