|
☆☆☆ 点击下载试题 ☆☆☆ 2018大庆市中考数学模拟试题 一、选择题：（每题3分，共30分） 1．下列运算正确的是（ ） A．a6÷a2=a3B．a6+a2=a8C．（a2）3=a6D．2a×3a=6a 2．已知地球上七大洲的总面积约为150000000km2，则数字150000000用科学记数法可以表示为（ ） A．1.5×106B．1.5×107C．1.5×108D．1.5×109 3．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ） A．  B． C． D． 4．若将函数y=2x2的图象向右平行移动1个单位，再向上平移5个单位，可得到的抛物线是（ ） A．y=2（x﹣1）2﹣5B．y=2（x﹣1）2+5C．y=2（x+1）2﹣5D．y=2（x+1）2+5 5．双曲线y=  （k≠0）经过（1，﹣4），下列各点在此双曲线上的是（ ）A．（﹣1，﹣4）B．（4，1）C．（﹣2，﹣2）D．（  ，﹣4 ）6．如图，点A、B、C是⊙O上的点，若∠ACB=35°，则∠AOB的度数为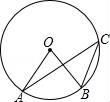（ ）  A．35°B．70°C．105°D．150° 7．如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向点C处测得AC=a，∠ACB=α，那么AB等于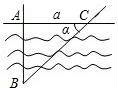（ ）  A．a•sinαB．a•tanαC．a•cosαD．  8．如图，△ABC中，∠ACB=70°，将△ABC绕点B按逆时针方向旋转得到△BDE（点D与点A是对应点，点E与点C是对应点），且边DE恰好经过点C，则∠ABD的度数为（ ）  A．30°B．40°C．45°D．50° 9．如图，直线l和双曲线  （k＞0）交于A、B两点，P是线段AB上的点（不与A、B重合），过点A、B、P分别向x轴作垂线，垂足分别是C、D、E，连接OA、OB、OP，设△AOC面积是S1，△BOD面积是S2，△POE面积是S3，则（ ） A．S1＜S2＜S3B．S1＞S2＞S3C．S1=S2＞S3D．S1=S2＜S3 10．某油箱容量为60L的汽车，加满汽油后行驶了100km时，油箱中的汽油大约消耗了  ，如果加满汽油后汽车行驶的路程为xkm，油箱中剩油量为yL，则y与x之间的函数解析式和自变量取值范围分别是（ ）A．y=0.12x，x＞0B．y=60﹣0.12x，x＞0 C．y=0.12x，0≤x≤500D．y=60﹣0.12x，0≤x≤500 二、填空题：（每题3分，共30分） 11．在Rt△ABC中，∠C=90°，AC=4，AB=5，则sinB的值是 ． 12．计算：  + ﹣3 = ．13．把多项式2x2y﹣8xy2+8y3分解因式的结果是 ． 14．不等式组  的解集是 ．15．已知二次函数y=﹣x2+mx+2的对称轴为直线x=  ，则m= ．16．已知扇形的圆心角为45°，弧长为3π，则此扇形的半径为 ． 17．如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则BC= ．  18．点A是反比例函数y=  第二象限内图象上一点，它到原点的距离为10，到x轴的距离为8，则k= ．19．已知：正方形ABCD的边长为2，点P是直线CD上一点，若DP=1，则tan∠BPC的值是 ． 20．如图，四边形ABCD中，对角线AC⊥BD于点O，且AO=BO=4，CO=8，∠ADB=2∠ACB，则四边形ABCD的面积为 ．  三、解答题：（21、22题7分，23题、24题8分，25-27题各10分） 21．先化简，再求代数式的值：  ，其中a=tan60°﹣2sin30°．22．如图，在小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上． （1）在图1中画一个以线段AB为一边的平行四边形ABCD，点C、D均在小正方形的顶点上，且平行四边形ABCD的面积为10； （2）在图2中画一个钝角三角形ABE，点E在小正方形的顶点上，且三角形ABE的面积为4，tan∠AEB=  ．请直接写出BE的长． 23．如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF． （1）判断四边形ABDF是怎样的四边形，并说明理由； （2）若AB=6，BD=2DC，求四边形ABEF的面积．  24．如图，在平面直角坐标系中，点O为坐标原点，△OAB的顶点B在x轴负半轴上，OA=OB=5，tan∠AOB=  ，点P与点A关于y轴对称，点P在反比例函数y= 的图象上．（1）求反比例函数的解析式； （2）点D在反比例函数y= 第一象限的图象上，且△APD的面积为4，求点D的坐标． 25．工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等． （1）该工艺品每件的进价、标价分别是多少元？ （2）若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件．若每件工艺品降价1元，则每天可多售出该工艺品4件．问每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元？ 26．如图，⊙O中弦AB⊥弦CD于E，延长AC、DB交于点P，连接AO、DO、AD、BC． （1）求证：∠AOD=90°+∠P； （2）若AB平分∠CAO，求证：AD=AB； （3）在（2）的条件下，若⊙O的半径为5，PB=  ，求弦BC的长． 27．如图所示，平面直角坐标系中，O为原点，抛物线y=﹣x2+2k（k≠0）顶点为C点，抛物线交x轴于A、B两点，且AB=CO； （1）求此抛物线解析式； （2）点P为第一象限内抛物线上一点，连接PA交y轴于点D，连接PC，设点P的横坐标为t，△PCD的面积为S，求S与t的函数关系式，并直接写出t的取值范围； （3）在（2）的条件下，连接AC，过点D作DE⊥y轴交AC于E，连接PE，交y轴于F，若5CF=3OF，求P点坐标．  2018大庆市中考数学模拟试题参考答案 一、选择题：（每题3分，共30分） 1．下列运算正确的是（ ） A．a6÷a2=a3B．a6+a2=a8C．（a2）3=a6D．2a×3a=6a 【考点】单项式乘单项式；合并同类项；幂的乘方与积的乘方；同底数幂的除法． 【分析】原式利用单项式乘以单项式法则，合并同类项法则，幂的乘方运算法则，以及同底数幂的乘法法则计算得到结果，即可作出判断． 【解答】解：A、原式=a4，错误； B、原式不能合并，错误； C、原式=a6，正确； D、原式=6a2，错误， 故选C 2．已知地球上七大洲的总面积约为150000000km2，则数字150000000用科学记数法可以表示为（ ） A．1.5×106B．1.5×107C．1.5×108D．1.5×109 【考点】科学记数法—表示较大的数． 【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数． 【解答】解：将150000000用科学记数法表示为1.5×108． 故选：C． 3．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ） A．  B． C． D． 【考点】中心对称图形；轴对称图形． 【分析】根据轴对称图形与中心对称图形的概念分别分析求解． 【解答】解：A、不是轴对称图形，是中心对称图形，故此选项错误； B、是轴对称图形，不是中心对称图形，故此选项错误； C、是轴对称图形，也是中心对称图形，故此选项正确； D、不是轴对称图形，也不是中心对称图形，故此选项错误． 故选：C． 4．若将函数y=2x2的图象向右平行移动1个单位，再向上平移5个单位，可得到的抛物线是（ ） A．y=2（x﹣1）2﹣5B．y=2（x﹣1）2+5C．y=2（x+1）2﹣5D．y=2（x+1）2+5 【考点】二次函数图象与几何变换． 【分析】抛物线平移不改变a的值． 【解答】解：原抛物线的顶点为（0，0），向右平行移动1个单位，再向上平移5个单位，那么新抛物线的顶点为（1，5）．可设新抛物线的解析式为y=2（x﹣h）2+k，代入人得：y=2（x﹣1）2﹣5． 故选B． 5．双曲线y=  （k≠0）经过（1，﹣4），下列各点在此双曲线上的是（ ）A．（﹣1，﹣4）B．（4，1）C．（﹣2，﹣2）D．（  ，﹣4 ）【考点】反比例函数图象上点的坐标特征． 【分析】将（1，﹣4）代入y= 即可求出k的值，再根据k=xy解答即可．【解答】解：∵双曲线y= （k≠0）经过（1，﹣4），∴k=1×（﹣4）=﹣4 四个选项中只有D  =﹣4符合，故选：D． 6．如图，点A、B、C是⊙O上的点，若∠ACB=35°，则∠AOB的度数为（ ）  A．35°B．70°C．105°D．150° 【考点】圆周角定理． 【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半． 【解答】解：由圆周角定理可得：∠AOB=2∠ACB=70°． 故选B． 7．如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向点C处测得AC=a，∠ACB=α，那么AB等于（ ）  A．a•sinαB．a•tanαC．a•cosαD．  【考点】解直角三角形的应用﹣方向角问题． 【分析】根据题意，可得Rt△ABC，同时可知AC与∠ACB．根据三角函数的定义解答． 【解答】解：根据题意，在Rt△ABC，有AC=a，∠ACB=α，且tanα=  ，则AB=AC×tanα=a•tanα， 故选B． 8．如图，△ABC中，∠ACB=70°，将△ABC绕点B按逆时针方向旋转得到△BDE（点D与点A是对应点，点E与点C是对应点），且边DE恰好经过点C，则∠ABD的度数为（ ）  A．30°B．40°C．45°D．50° 【考点】旋转的性质． 【分析】先根据旋转的性质得∠ABD=∠CBE，∠E=∠ACB=70°，BC=BE，则根据等腰三角形的性质得∠BCE=∠E=70°，再利用三角形内角和计算出∠CBE，从而得到∠ABD的度数． 【解答】解：∵△ABC绕点B按逆时针方向旋转得到△BDE（点D与点A是对应点，点E与点C是对应点）， ∴∠ABD=∠CBE，∠E=∠ACB=70°，BC=BE， ∴∠BCE=∠E=70°， ∴∠CBE=180°﹣70°﹣70°=40°， ∴∠ABD=40°． 故选B． 9．如图，直线l和双曲线  （k＞0）交于A、B两点，P是线段AB上的点（不与A、B重合），过点A、B、P分别向x轴作垂线，垂足分别是C、D、E，连接OA、OB、OP，设△AOC面积是S1，△BOD面积是S2，△POE面积是S3，则（ ） A．S1＜S2＜S3B．S1＞S2＞S3C．S1=S2＞S3D．S1=S2＜S3 【考点】反比例函数系数k的几何意义． 【分析】由于点A在y= 上，可知S△AOC= k，又由于点P在双曲线的上方，可知S△POE＞k，而点B在y=上，可知S△BOD=k，进而可比较三个三角形面积的大小【解答】解：如右图， ∵点A在y= 上，∴S△AOC= k，∵点P在双曲线的上方， ∴S△POE＞ k，∵点B在y= 上，∴S△BOD= k，∴S1=S2＜S3． 故选；D．  10．某油箱容量为60L的汽车，加满汽油后行驶了100km时，油箱中的汽油大约消耗了  ，如果加满汽油后汽车行驶的路程为xkm，油箱中剩油量为yL，则y与x之间的函数解析式和自变量取值范围分别是（ ）A．y=0.12x，x＞0B．y=60﹣0.12x，x＞0 C．y=0.12x，0≤x≤500D．y=60﹣0.12x，0≤x≤500 【考点】根据实际问题列一次函数关系式． 【分析】根据题意列出一次函数解析式，即可求得答案． 【解答】解：因为油箱容量为60L的汽车，加满汽油后行驶了100km时，油箱中的汽油大约消耗了 ，可得：  L/km，60÷0.12=500（km），所以y与x之间的函数解析式和自变量取值范围是：y=60﹣0.12x，（0≤x≤500）， 故选D． 二、填空题：（每题3分，共30分） 11．在Rt△ABC中，∠C=90°，AC=4，AB=5，则sinB的值是  ．【考点】锐角三角函数的定义． 【分析】根据正弦的定义计算即可． 【解答】解：∵∠C=90°，AC=4，AB=5， ∴sinB=  =，故答案为： ．12．计算：  + ﹣3 = 3 ．【考点】二次根式的加减法． 【分析】首先把二次根式化成最简二次根式，然后再合并即可． 【解答】解：原式=4  +2﹣3=3，故答案为：3 ．13．把多项式2x2y﹣8xy2+8y3分解因式的结果是 2y（x﹣2y）2 ． 【考点】提公因式法与公式法的综合运用． 【分析】根据提公因式法，可得完全平方公式，根据完全平方公式，可得答案． 【解答】解：原式=2y（x2﹣4xy+4y2） =2y（x﹣2y）2， 故答案为：2y（x﹣2y）2． 14．不等式组  的解集是 3≤x＜4 ．【考点】解一元一次不等式组． 【分析】分别求出不等式组中两不等式的解集，找出解集的公共部分即可． 【解答】解：  ，由①得：x＜4； 由②得：x≥3， 则不等式组的解集为3≤x＜4． 故答案为：3≤x＜4 15．已知二次函数y=﹣x2+mx+2的对称轴为直线x=  ，则m=  ．【考点】二次函数的性质． 【分析】把二次函数解析式化为顶点式可用m表示出其对称轴，再由条件可得到关于m的方程，可求得m的值． 【解答】解：∵y=﹣x2+mx+2=﹣（x﹣  ）2+ +2，∴二次函数对称轴为直线x= ，∵二次函数的对称轴为直线x= ，∴ =，解得m= ，故答案为： ．16．已知扇形的圆心角为45°，弧长为3π，则此扇形的半径为 12 ． 【考点】弧长的计算． 【分析】根据弧长公式l=  代入求解即可．【解答】解：∵l= ，∴r=  =12．故答案为12． 17．如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则BC= 6 ． 【考点】圆周角定理；解直角三角形． 【分析】由已知可证∠BDA=30°；根据BD为⊙O的直径，可证∠BAD=90°，得∠DBC=30°，即∠DBA=60°，所以BC=AD=6． 【解答】解：连接CD． ∵△ABC内接于⊙O，∠BAC=120°，AB=AC， ∴∠CBA=∠BCA=30°． ∴∠BDA=∠ACB=30°． ∵BD为⊙O的直径， ∴∠BAD=90°，∠BDA=30°， ∴∠DBC=90°﹣30°﹣30°=30°， ∴∠DBA=60°，∠BDC=60°， ∴BC=AD=6． 18．点A是反比例函数y= 第二象限内图象上一点，它到原点的距离为10，到x轴的距离为8，则k= ±48 ．【考点】反比例函数图象上点的坐标特征． 【分析】由题意点A是反比例函数图象上一点，它到原点的距离为10，到x轴的距离为8，根据勾股定理可得其道y轴的距离为6，用待定系数法求出函数的表达式． 【解答】解：设反比例函数的解析式为：y= ，设A点为（a，b）， ∵点A是反比例函数图象上一点，它到原点的距离为10， ∴a2+b2=100①， ∵点A到x轴的距离为8， ∴|b|=8，把b值代入①得， ∴|a|=6， ∴A（6，8）或（﹣6，﹣8）或（﹣6，8）或（6，﹣8）， 把A点代入函数解析式y= ，得k=±48， 故答案为：±48． 19．已知：正方形ABCD的边长为2，点P是直线CD上一点，若DP=1，则tan∠BPC的值是 2或  ．【考点】锐角三角函数的定义；勾股定理；正方形的性质． 【分析】本题可以利用锐角三角函数的定义、勾股定理以及正方形的性质求解． 【解答】解：此题有两种可能： （1）∵BC=2，DP=1， ∠C=90°， ∴tan∠BPC=  =2；（2）∵DP=1，DC=2， ∴PC=3， 又∵BC=2，∠C=90°， ∴tan∠BPC=  = ．故答案为：2或 ．  20．如图，四边形ABCD中，对角线AC⊥BD于点O，且AO=BO=4，CO=8，∠ADB=2∠ACB，则四边形ABCD的面积为 42 ．  【考点】相似三角形的判定与性质． 【分析】如图，作∠ADO的平分线DP交AC于P，作PE⊥AD于E．由△POD∽△BOC，得  = ，设OP=x，推出OD=2x，由PE⊥AD，PO⊥DO，∠PDE=∠PDO，推出PE=OP，由 = = ，推出 = ，推出AD=2（4﹣x），在Rt△ADO中，根据AD2=AO2+DO2，可得4（4﹣x）2=4x2+42，求出x的值，再根据S四边形ABCD=S△ABD+S△BDC= •BD•AO+•BD•OC=•BD（OA+OC）计算即可．【解答】解：如图，作∠ADO的平分线DP交AC于P，作PE⊥AD于E．  ∵∠ADO=2∠BCO， ∴∠PDO=∠BCO， ∵∠POD=∠BOC， ∴△POD∽△BOC， ∴  = ，设OP=x，∴  = ，∴OD=2x， ∵PE⊥AD，PO⊥DO，∠PDE=∠PDO， ∴PE=OP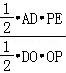， ∴  = = ，∴  = ，∴AD=2（4﹣x）， 在Rt△ADO中，∵AD2=AO2+DO2， ∴4（4﹣x）2=4x2+42， ∴x=  ，∴OD=3， ∴S四边形ABCD=S△ABD+S△BDC=  •BD•AO+•BD•OC=•BD（OA+OC）=×7×12=42．故答案为42． 三、解答题：（21、22题7分，23题、24题8分，25-27题各10分） 21．先化简，再求代数式的值：  ，其中a=tan60°﹣2sin30°．【考点】分式的化简求值；特殊角的三角函数值． 【分析】分别化简分式和a的值，再代入计算求值． 【解答】解：原式=  ．当a=tan60°﹣2sin30°= ﹣2×= 时，原式=  ．22．如图，在小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上． （1）在图1中画一个以线段AB为一边的平行四边形ABCD，点C、D均在小正方形的顶点上，且平行四边形ABCD的面积为10； （2）在图2中画一个钝角三角形ABE，点E在小正方形的顶点上，且三角形ABE的面积为4，tan∠AEB=  ．请直接写出BE的长． 【考点】作图—应用与设计作图；勾股定理；平行四边形的判定；解直角三角形． 【分析】（1）由图可知A、B间的垂直方向长为2，要使构建平行四边形ABCD的面积为10，则可以在A的水平方向取一条长为5的线段，可得点C； （2）由图可知A、B间的垂直方向长为2，要使构建的钝角三角形ABE面积为4，则可以在A的水平方向取一条长为4的线段，可得点E，且tan∠AEB= ，BE的长可以根据勾股定理求得．【解答】解：（1）如图1所示； （2）如图2所示；  BE=  =2 ．23．如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF． （1）判断四边形ABDF是怎样的四边形，并说明理由； （2）若AB=6，BD=2DC，求四边形ABEF的面积． 【考点】平行四边形的判定与性质；等边三角形的判定与性质；勾股定理． 【分析】（1）等边三角形的三边相等，三个角也相等，根据等边三角形的性质能证明AF∥BD，AB∥FD，所以四边形ABDF是怎样的四边形． （2）过点E作EG⊥AB于点G，可求出EG的长，面积可求． 【解答】解：（1）∵CD=CE，∠BCA=60°， ∴△DEC是等边三角形， ∴∠DEC=∠EDC=∠AEF=60°， ∵△ABC是等边三角形， ∴∠ABC=60°， ∴AB∥DF， ∵EF=AE，∠AEF=60°， ∴△AEF是等边三角形， ∴∠AFD=60°， ∴BD∥AF， ∴四边形ABDF是平行四边形； （2）∵四边形ABDF是平行四边形， ∴EF∥AB，且EF≠AB， ∴四边形ABEF是梯形． 过点E作EG⊥AB于点G， ∵BD=2DC，AB=6， ∴AE=BD=EF=4， ∵∠AGE=90°，∠BAC=60°， ∴∠AEG=30°， ∴AG= AE=2，EG=  = =2 ，∴S= （4+6）×2=10． 24．如图，在平面直角坐标系中，点O为坐标原点，△OAB的顶点B在x轴负半轴上，OA=OB=5，tan∠AOB=  ，点P与点A关于y轴对称，点P在反比例函数y= 的图象上．（1）求反比例函数的解析式； （2）点D在反比例函数y= 第一象限的图象上，且△APD的面积为4，求点D的坐标． 【考点】待定系数法求反比例函数解析式；反比例函数系数k的几何意义；等腰三角形的性质；解直角三角形． 【分析】（1）首先过点A作AC⊥x轴，由线段OA=5，点B在x轴负半轴上，且tan∠AOB=  ，可求得点A的坐标，进而求得P的坐标，然后利用待定系数法求得反比例函数的解析式；（2）根据三角形面积求得D的纵坐标，代入反比例函数式，即可求得横坐标． 【解答】解：（1）过点A作AC⊥x轴， ∵在Rt△AOC中，tan∠AOB=  =，设AC=3x，OC=4x， ∵OA=5， 在Rt△AOD中，根据勾股定理解得AC=3，OC=4， ∴A（﹣4，3）， ∵点P与点A关于y轴对称， ∴P（4，3）， 把P（4，3）代入反比例函数y= 中，解得：k=12， 则反比例函数的解析式为y=  ；（2）∵A（﹣4，3），P（4，3）， ∴AP=8， ∵△APD的面积为4， ∴D的纵坐标为4或2， 把y=4代入y= 求得，x=3，把y=2代入y=  求得，x=6，∴D的坐标为（3，4）或（6，2）．  25．工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等． （1）该工艺品每件的进价、标价分别是多少元？ （2）若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件．若每件工艺品降价1元，则每天可多售出该工艺品4件．问每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元？ 【考点】二次函数的应用；二元一次方程组的应用． 【分析】（1）根据“每件获利45元”可得出：每件标价﹣每件进价=45元；根据“标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等”可得出等量关系：每件标价的八五折×8﹣每件进价×8=（每件标价﹣35元）×12﹣每件进价×12． （2）可根据题意列出关于总利润和每天利润的二次函数，以此求出问题． 【解答】解：（1）设该工艺品每件的进价是x元，标价是y元． 依题意得方程组：  解得：  ．故该工艺品每件的进价是155元，标价是200元． （2）设每件应降价a元出售，每天获得的利润为W元． 依题意可得W与a的函数关系式：W=（45﹣a）， W=﹣4a2+80a+4500， 配方得：W=﹣4（a﹣10）2+4900， 当a=10时，W最大=4900． 故每件应降价10元出售，每天获得的利润最大，最大利润是4900元． 26．如图，⊙O中弦AB⊥弦CD于E，延长AC、DB交于点P，连接AO、DO、AD、BC． （1）求证：∠AOD=90°+∠P； （2）若AB平分∠CAO，求证：AD=AB； （3）在（2）的条件下，若⊙O的半径为5，PB= ，求弦BC的长．【考点】圆的综合题． 【分析】（1）由圆周角定理可知∠AOD=2∠ACD，结合三角形的外角的性质可得到∠AOD=2∠CDP+2∠P，接下来，依据∠CAE=∠CDP，可将∠AOD转化为∠CDP、∠CAE、2∠P，最后根据∠CAE+∠CDP+∠P=90°可证得问题的答案； （2）延长AO交BD与点F．首先证明∠AFB=∠AEC=90°，接下来，再证明△AFD≌△ADB，由全等三角形的性质可得到AB=AD； （3）延长AO交BD与点G交⊙O与点F，连结BF、OB．依据弧、弦、弦心距之间的关系可知BC=FB，接下来，证明OB∥AP，依据平行线分线段成比例定理可知  ，故此可得到 = ，在△OBG中由勾股定理可得到OG=4，BG=3，从而可求得GF=1，在Rt△BGF中，由勾股定理得可求得BF的长，于是得到BC的长．【解答】解：（1）∵∠CDP+∠P=∠ACD，∠AOD=2∠ACD， ∴∠AOD=2∠CDP+2∠P． ∵∠CAE=∠CDP， ∴∠AOD=∠CDP+∠CAE+∠P+∠P ∵AB⊥CD， ∴∠CAE+∠ACD=90°． ∴∠CAE+∠CDP+∠P=90°． ∴∠AOD=90°+∠P． （2）如图1所示：延长AO交BD与点F．  ∵AB平分∠CAO， ∴∠CAE=∠BAF． 又∵∠ACE=∠ABF， ∴△ACE∽△ABF． ∴∠AFB=∠AEC=90°． ∴AF⊥BD． ∴FD=BF． 在△ABF和△ADF中  ，∴△AFD≌△ADB． ∴AB=AD． （3）延长AO交BD与点G交⊙O与点F，连结BF、OB．  ∵∠CAB=∠OAB， ∴  ．∴BC=FB． ∵OA=OB， ∴∠OAB=∠OBA． ∴∠CAB=∠OBA． ∴OB∥AP． ∴  ．∴  =．设OG=4k，GB=3k． 在△OBG中，由勾股定理可知：（4k）2+（3k）2=25． 解得：k=1（负值已舍去）． ∴OG=4，BG=3． ∴GF=1． 在Rt△BGF中，由勾股定理得：BF=  = ．∴BC= ．27．如图所示，平面直角坐标系中，O为原点，抛物线y=﹣x2+2k（k≠0）顶点为C点，抛物线交x轴于A、B两点，且AB=CO； （1）求此抛物线解析式； （2）点P为第一象限内抛物线上一点，连接PA交y轴于点D，连接PC，设点P的横坐标为t，△PCD的面积为S，求S与t的函数关系式，并直接写出t的取值范围； （3）在（2）的条件下，连接AC，过点D作DE⊥y轴交AC于E，连接PE，交y轴于F，若5CF=3OF，求P点坐标．  【考点】二次函数综合题． 【分析】（1）由题意点B坐标（k，0），代入抛物线y=﹣x2+2k得﹣k2+2k=0，解方程即可． （2）如图1中，作PM⊥AB于M．设点P坐标（t，﹣t2+4），由OD∥PM，得  = ，求出OD，即可解决问题．（3））如图2中，作PM⊥AB于M，ED的延长线交PM于N．先求出直线AC解析式，得到点E坐标，推出DE=DN，推出DF是△EPN的中位线，根据PN=2DF，列出方程即可解决问题． 【解答】解：（1）∵抛物线y=﹣x2+2k（k≠0）顶点为C点， ∴点C坐标（0，2k， ∵AB=CO，OA=OB， ∴点B坐标（k，0），代入抛物线y=﹣x2+2k得﹣k2+2k=0， ∴k=2或0（舍弃）， ∴抛物线解析式为y=﹣x2+4． （2）如图1中，作PM⊥AB于M．  设点P坐标（t，﹣t2+4）， ∵OD∥PM， ∴ =，∴  = ，∴OD=4﹣2t， ∴CD=4﹣（4﹣2t）=2t， ∴S= •2t•t=t2，（0＜t＜2）（3）如图2中，作PM⊥AB于M，ED的延长线交PM于N．  ∵∠NDO=∠DOM=∠NMO=90°， ∴四边形OMND是矩形， ∴DN=OM=t ∵OC=4，5CF=3OF，设CF=3k，OF=5k， 则8k=4， ∴k= ，∴CF= ，OF= ，∵直线AC的解析式为y=2x+4，D（0，4﹣2t），DE⊥OC， ∴E（﹣t，4﹣2t）， ∴ED=DN=OM=t ∵DF∥PN， ∴EF=FP， ∴PN=2DF， ∴﹣t2+4﹣（4﹣2t）=2[ ﹣（4﹣2t）]，∴t2+2t﹣3=0， ∴t=1或﹣3（舍弃）， ∴点P坐标（1，3）． 2017年3月16日 (责任编辑：admin) |