|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看 2018年郑州市中考数学试题 一、数学试题选择题(每小题3分,共24分)在每小题四个选项中,只有一项是符合题目要求 1.给出四个数0, A.-1 B. 2.有一种圆柱体茶叶筒如图所示,则它的左视图是() 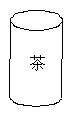 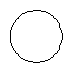 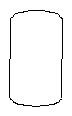 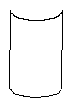  A. B.C. D. 3.把不等式组 A.  B. B.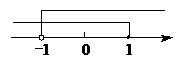 C. 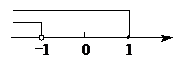 D. D.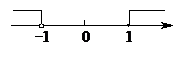    4.如图,已知△ABC,AB 4.如图,已知△ABC,AB A. B. C. D. 5.马老 间写在纸上用于统计,下面是全班45名学生单程所花时间(单位:分)与对应人数 (单位:人)的统计表,则关于这45名学生单程所花时间的数据的中位数是()
A.15 B.20 C.25 D.30 6.如图,在一单位长度为1的方格纸上,依如图所示的规律,设定点A1,A2,A3,A4, A5,A6,A7,…An,连接点O,A1,A2组成三角形,记为△1,连接 角形,记为△2,…,连接O,An,An+1组成三角形,记为△n(n为正整数),请你推 断,当n为10时,△n的面积=()平方单位. A.45 B.55 C.66 D.100   第6题图 第8题图 7.郑徐客运专线(简称郑徐高铁),即郑州至徐州高速铁路,是《国家中长期铁路网 规划》中“四纵四横”之一的徐兰客运专线的重要组成部分.2016年7月将要开通运 营.高铁列车从郑州到徐州的运行时间比原普通车组的运行时间要快约1.4个小 时.已知郑州到徐州的铁路长约为361千米,原普通车组列车的平均速度为x千米/ 时,高铁列车的平均速度比原普通车组列车增加了145千米/时,依题意,下面所列 方程正确的是() A. C. 8.如图,边长为6 线段EC绕点C逆时针转60°得到FC,连接DF.则在点E运 A.6 B.3 C.2 D.1.5 二、填空题(每小题3分,共21分) 9.计算 10.如图,已知直线AB∥CD,直线EG垂 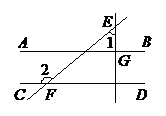 11.微信根据移动ID所带来的数据,发布了“微信用户春节迁徙数据报告”.该报告显 示,2016年1月24日春运首日至2月4日期间,人口流入最多的省份是河南,作为劳务 输出大省,河南约有313万微信用户在春节期间返乡,313万用科学记数法可表示为_________. 12.一个不透明的盒子里有4个除颜色外其他完全相同的小球,其中每个小球上分别标有1,-1,-2,-3四个不同的数字,每次摸球前先将盒子里的球摇匀,任意摸出一 个球记下数字后再放回盒子,那么两次摸出的小球上两个数字乘积是负数的概率为_________. 13.反比例函数 14.如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4,O是AB的中点,以O为圆心, 线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为__________平方单位.   第14题图 第15题图 15.已知一个矩形纸片O C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C 落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为 ____________. 三、解答题(共75分) 16.(8分)先化简 选取一个合适的数代入求值. 17.(9分)今年3月12日,某校九年级部分学生参加植树节活动,以下是根据本次植树活动的有关数据制作的统计图的一部分.请根据统计图所提供的有关信息,完成下列问题:  (1)参加植树的学生共有_______人,植树的众数是_______棵; (2)请将该条形统计图补充完整; (3)参加植树的学生平均每人植树多少棵?(保留整数) 18.(9分)如图,已知 (1)求证:△ABC≌△ABF; (2)当∠CAB=______时,四边形ADFE为菱形; (3)当AB=_______时,四边形ACBF为正方形.  19.(9分)已知:关于x的一元二次方程 (1)求k的取值范围; (2)当k取最大整数值时,用合适的方法求该方程的解. 20.(9分)图1是小 (1)求AB的长(精确到0.01米); (2)若测得EN=0.8米,计算小明头顶由N点运动到M点的路径的长度(结果保留π).   图2
其中方案一所示图形是顶点在原点的抛物线的一部分,方案二所示的图形是射线.设推销员销售产品的数量为x(件),付给推销员的月报酬为y(元). (1)分别求两种方案中y关于x的函数关系式; (2)当销售量达到多少件时,两种方案的月报酬差额将达到3 800元? (3)若公司决定改进“方案二”:基本工资1 200元,每销售一件产品再增加报酬m元,当推销员销售量达到40件时,方案二的月报酬不低于方案一的月报酬.求m至少增加多少元? 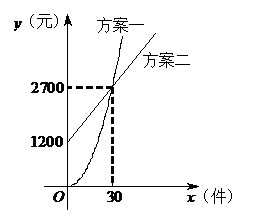
DE交AC于点G,DF经过点C. (1)求∠ADE的度数; (2)如图2,将图1中的∠EDF绕点D顺时针方向旋转角α(0°<α<60°),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2,DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求 (3)若图1中的∠B=β(60°<β<90°), (2)中的其余条件不变,请直接写出  
B(3,0)、点C三点.(1)求抛物线的表达式. (2)点D(2,m)在第一象限的抛物线上,连接BC,BD.在对称轴左侧的抛物线 上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由. 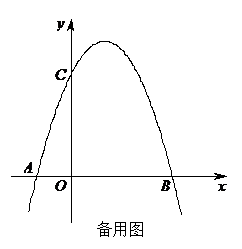  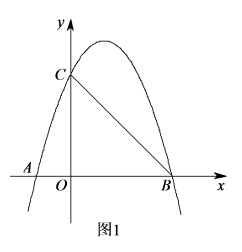 (3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速 (3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′ 与△BCD重叠的面积记为S,设平移的时间为t秒,直接写出S与t之间的函数关系式. 2018年郑州中考数学模拟试题 参考答案 一、选择题(每小题3分,共24分)
二、填空题(每小题3分,共21分) 9. 2; 10. 140; 11. 14. 三、解答题(共75分) 16. 解:原式= = = 因为a为整数且﹣2≤a≤2, 通过题意可知 所以把 (答案不唯一) 17.解:(1)50;2;………………4分 (2)图略;………………6分 (3) 所以参加植树的学生平均每人植树3棵.………………9分 18.(1)证明: ∵AB∥EF, ∴∠AFE=∠FAB,∠CAB=∠AEF.………………2分 ∵AE=AF, 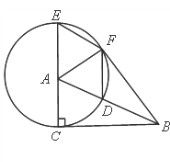 ∴∠AEF=∠AFE. ∴∠AEF=∠AFE.∴∠CAB=∠FAB.………………4分 ∵AB=AB,AC=AF, ∴△ABC≌△ABF.………………5分 (2)60°;………………7分 (3) 19. 解:(1)∵ 关于 ∴ 解得 (2)∵ ∴ 符合条件的最大整数 此时方程为 ∴ 20.解:(1)作AF⊥BC于点F.∴∠AFB=90°. ∴∠AFB=∠AFC =∠ADC =90°. ∴四边形ADCF是矩形. …………1分 ∴FC=AD.[来# 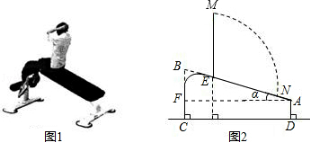 ∴BF= BC﹣CF =BC﹣AD=0.64-0.24=0.4米,…………3分 ∴BF= BC﹣CF =BC﹣AD=0.64-0.24=0.4米,…………3分∴AB=BF÷sin18°=0.4÷0.31≈1.29米;………………5分 (2)∵∠NEM=90°+18°=108°,…………………………7分 ∴弧NM长为 答: AB的长约为1.29米; 弧NM长为 21.解:(1)设 解得:a=3, ∴ 设y2=kx+b,把(0,1200),(30,2700)代入得: 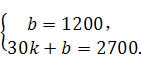 解得: 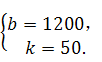 ∴y2=50x+1200.…………………………4分 [来源:ZXXK] (2)由题意得:3x2﹣(50x+1200)=3800, 解得: 答:当销售达到50件时,两种方案月报酬差额将达到3800元. (3)当销售员销售产量达到40件时, 方案一的月报酬为:3×402=4800. 方案二的月报酬为:(50+m)×40+1200=40m+3200.………8分 由题意得:4800≤40m+3200.[来 解得:m 所以至少增加40元.…………………………10分 22.解:(1)∵∠ACB=90°,D为AB的中点, ∴CD=DB, ∴∠DCB=∠B.…………………………1分 ∵∠B=60°, ∴∠DCB=∠B=∠CDB=60°.…………………………2分 ∴∠CDA=120°. ∵∠EDC=90°, ∴∠ADE=30°;…………………………4分 (2)∵∠C=90°,∠MDN=90°, ∴∠DMC+∠CND=180°. ∵∠DMC+∠PMD=180°, ∴∠CND=∠PMD. 同理∠CPD=∠DQN. ∴ 过点D分别做DG⊥AC于G,DH⊥BC于H.  可知DG,DH分别为△PMD和△QND的高. ∴ ∵DG⊥AC于G,DH⊥BC于H, ∴DG∥BC. 又∵D为AB中点, ∴G为AC中点. ∵∠C=90°, ∴四边形CGDH 为矩形,有CG=D Rt△AGD中, 即 (3) 23.解:(1)将点A(﹣1,0)、B(3,0)的坐标分别代入抛物线y=ax2+bx+3(a≠0),得 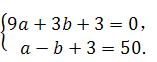 解得:a=﹣1,b=2. 故抛物线解析式为:y=﹣x2+2x+3.……………………3分 (2)存在. 将点D(2,m)代入抛物线解析式得:m=3, ∴D(2,3).……………………4分 令x=0,y=3, ∴C(0,3). ∴OC=OB. ∴∠OCB=∠CBO=45°.………………………………5分 如下图,设BP交y轴于点G, 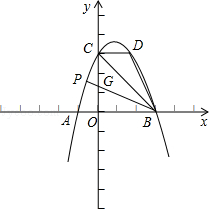 ∵CD∥x轴,∴∠DCB=∠BCO=45°. 在△CDB和△CGB中:  ∴△CDB≌△CGB(ASA). ∴CG=CD=2. ∴OG=1. ∴点G(0,1). ……………………7分 设直线BP:y=kx+1. 代入点B(3,0), ∴k=﹣ ∴直线BP:y=﹣ 联立直线BP和二次函数解析式: 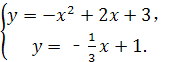 解得: 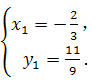 或 或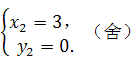 ∴P( (3)直线BC:y=﹣x+3,直线BD:y=﹣3x+9. 当0≤t≤2时,如下图: 设直线C′B′:y=﹣(x﹣t)+3. 联立直线BD求得F( 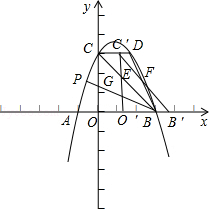 S=S△BCD﹣S△CC′E﹣S△C′DF = 整理得:S =﹣ 当 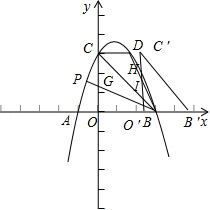 H(t,﹣3t+9),I(t,﹣t+3) S=S△HIB= 整理得:S=t2﹣6t+9(2 综上所述: 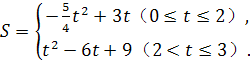 ……………………11分 ……………………11分(责任编辑:admin) |
