|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看 2018年忻州中考数学押题卷 题型一数学问题
A.一元一次方程B.二元一次方程组 C.一元二次方程D.分式方程
A.勾股定理 B一次函数 C.一元一次方程的实际应用 D.二元一次方程的实际应用 题型二 数学思想 1.问题:“如图,已知点 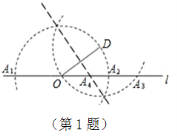 A.归纳与演绎 A.归纳与演绎B.分类讨论 C.数形结合 D.转化与化归
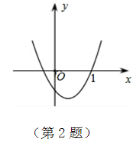 ( ) ( ) A.换元法 B.配方法 C.数形结合法 D.分类讨论法 题型三 跨试题
A.1 m B.1.5 mC.2 mD.2.5 m
重难点题型猜押 命题点一 图形操作题 1.将一张矩形纸按照如图方式对这两次后,沿着图中的虚线剪开,得到、两部分,将展开后得到的平面图形是( ) 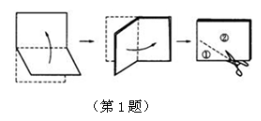
 命题点二规律探索题
 (第1题) A.17 B.18 C.19 D.20 2.下列图形都是由同样大小的黑点按一定的规律组成,其中第个图形中一共有4个黑点,第个图形中一共有9个黑点,第个图形中一共有14个黑点,…,则第⑩个图形中黑点的个数是 () 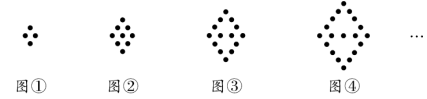 (第2题) A.44B.48C.49 D.54
命题点三 阴影部分面积计算

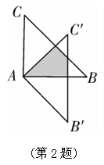 命题点四猜想证明题
初步探究:(1)如图①,当点 解决问题:(2)如图②,当点 类比延伸:(3)如图③,当点 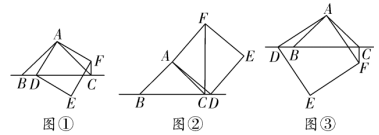 (第1题)
问题情境:数学活动课上,老师提出了一个问题:已知△ (1)独立思考:请解答老师提出的问题; (2)提出问题:一小组受此问题的启发,提出问题,如图②,若点 (3)问题拓展:老师要求其他小组向一小组同学学习,仿照前两种情况提出问题,二小组提出问题:如图③,若  (第2题) 名校模拟题 命题点一 数学问题与数学思想 1.如图,“毕达哥拉斯树”是由毕达哥拉斯画出来的一个可以无限延展的图形,这一图形反映的数学原理是( )
C.平行线分线段成比例 D.垂径定理 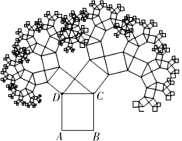 (第1题) 命题点二 跨试题
2.阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.公元前3世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来,人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:阻力×阻力臂=动力×动力臂(如图).  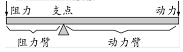 图① 图② (第2题) 问题解决: 若工人师傅欲用撬棍撬动一块大石头,已知阻力和臂力不变,分别为1500 N和0.4 m. (1)动力F(N)与动力臂 (2)若想使动力F(N)不超过题(1)中所用力的一半,则动力臂至少要加长多少? 数学思考: (3)请用数学知识解释:我们使用撬棍,当阻力与阻力臂一定时,为什么动力臂越长越省力. 命题点三 尺规作图
(1)  实践与操作: 利用尺规按下列要求作图吧,并在图中标明相应的字母(保留作图痕迹,不写作法). 实践与操作: 利用尺规按下列要求作图吧,并在图中标明相应的字母(保留作图痕迹,不写作法).作BC边上的高AD ; 作△ABC的角平分线BE ; (2)综合与运用: 若△ABC中AB=AC且∠CAB=36 结论1:____________________________;(关于角) 结论2:____________________________;(关于线段) 结论3:____________________________.(关于三角形)
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法). 作∠A的平分线AD,交BC与点E; 经过点B作AD的垂线交AD于点F; 连接CF. (2)综合与应用: 若△ABC是直角三角形,∠ABC=  (第2题) 命题点四 猜想证明题 1.问题情景: 1节数学课后,老师布置了一道课后练习题: 如图,已知在Rt△ABC中,AC =BC,∠ACB =90°,CD⊥AB于点D ,点E、点F分别在AD和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF. 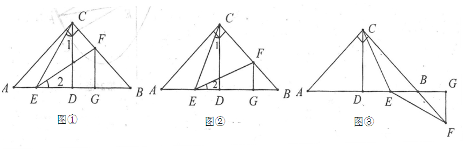 (第1题) (1)阅读理解,完成解答:本题证明的思路可用下列框图表示: 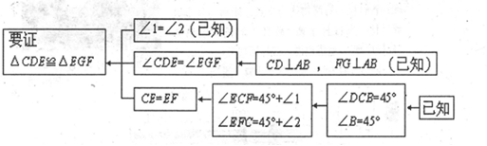 根据上述思路,请你完整地书写这道练习题的证明过程; (2)特殊位置,证明结论:如图②,若CE平分∠ACD,其余条件不变,判断AE和BF的数量关系,并说明理由; (3)知识迁移,探究发现:如图③,已知Rt△ABC中,AC =BC, ∠ACB =90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上,且EC =EF,请直接写出BF与AE的数量关系.(不必写解答过程) 命题点五函数动态探究题 1.如图,已知二次函数 (1)求二次函数的表达式; (2)点P是线段AB上的一动点(点P和点A,B不重合),过点P作PE∥AD交BD于E,连接DP,当△DPE的面积最大时,求点P的坐标; (3)若直线AD与 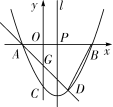 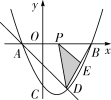 (第1题)(备用图) 2018年忻州中考数学押题卷参考答案 特殊题型猜押 题型一数学问题 【答案】1.B2.A 题型二 数学思想 【答案】1.B2.C 题型三 跨试题 【答案】1.C【解析】 已知视力检测时要求被测的人与视力表的距离为5 m,但房间空间太小,可利用平面镜成像特点,人与视力表的像的距离为5 m,如解图所示:因为视力表距平面镜3 m所以视力表在平面镜中所成的像距离平面镜为3 m,所以人距平面镜应为5 m-3 m=2 m. 
重难点题型猜押 命题点一 图形操作题 【答案】1.D 2.a2-b2=(a+b)(a-b)【解析】左边图形中,阴影部分的面积=a2-b2,右边图形中,阴影部分的面积=(a +b)(a -b),∵两个图形中的阴影部分的面积相等,∴a2-b2=(a +b)(a -b). 命题点二规律探索题 【答案】1.C【解析】第一个图形火柴棒的根数为2×1+1=3,第二个图形火柴棒的根数为2×2+1=5,第三个图形火柴棒的根数为2×3+1=7,第四个图形火柴棒的根数为2×4+1=9,由此可得第n个图形火柴棒的根数为2n+1,第九个图形火柴棒的根数为2×9+1=19. 2.C【解析】观察图形知:第个图形有5×(1+1)-6=4个黑点,第个图形有5×(2+1)-6=9个黑点,第个图形有5×(3+1)-6=14个黑点,第④个图形有5×(4+1)-6=19个黑点,
命题点三阴影部分面积计算 【答案】1. ∴ 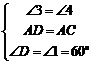 ,∴△ ,∴△∴四边形 S扇形AEF- S△ACD 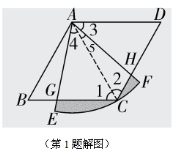 2. 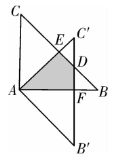 (第2题解图) 命题点四猜想证明题 【答案】1.(1)证明:①∵△ ∴ ∵四边形 ∴ ∵ ∴ 即 ∴△ ∴ ②由①知 ∴ ∴ (2)解:线段 (3)解:线段 理由如下:同理可证△ ∴ ∵ ∴ ∴
【解法提示】∵△ ∴ ∵ ∴ ∴ ∵ ∴ ∴ ∴ (2)猜想 证明:如解图①,过点 ∵△ 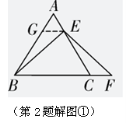 ∴ ∴又∵ ∴ 又∵ ∴ 在△ 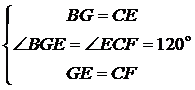 , ,∴△ ∴ (3) 【解法提示】如解图②,过点 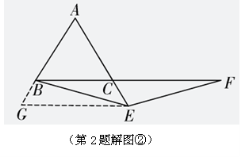 ∵△ ∵△∴ 又∵ ∴ 又∵ ∴△ ∴ 又∵ ∴ 又∵ ∴在△  , ,∴△ ∴ 名校模拟题 命题点一 数学问题与数学思想 【答案】B 命题点二 跨试题 【答案】1.C 2.解:(1)根据“杠杆定律”有 当 因此,撬动石头需要400 N的力. (2)由(1)可知 当 因此,若用力不超过400N的一半,则动力臂至少要加长1.5m. (3)因为撬棍工作遵循“杠杆定律”,当阻力与阻力臂一定时,其乘积为常数.设其为k,则动力F与臂力 命题点三 尺规作图
作出线段BE如解图; 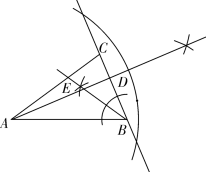 (第1题解图) (2)结论1:例如,∠C =72°,∠ABC =72°,∠C =∠ABC,∠AEB=108°等;结论2:  等;结论3:△ABE是等腰三角形,△BCE ∽△ABC等; 等;结论3:△ABE是等腰三角形,△BCE ∽△ABC等;
(2)3 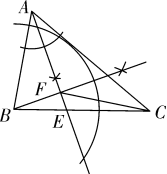 (第2题解图) 命题点四猜想证明题
∴∠A =∠B =45°, ∵CD⊥AB, ∴∠CDB=90°, ∴∠DCB=45°, ∵∠ECF =∠DCB +∠1=45°+∠1,∠EFC =∠B+∠2=45°+∠2, ∠1=∠2, ∴∠ECF =∠EFC, ∴CE =EF, ∵CD⊥AB,FG⊥AB, ∴∠CDE =∠EGF=90°, 在△CDE和△EGF中, 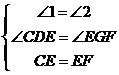 , ,∴△CDE≌△EGF(AAS); (2)证明:由(1)可得CE =EF,∠A=∠B, ∵CE平分∠ACD, ∴∠ACE=∠1, ∵∠1=∠2, ∴∠ACE =∠2, 在△ACE和△BEF中, 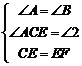 , ,∴△ACE≌△BEF(AAS), ∴AE=BF ; (3) 命题点五 函数动态探究题
∴二次函数 又∵点A的坐标为(-2,0), 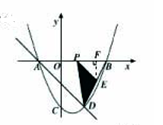 ∴点B的坐标为(4,0), ∴点B的坐标为(4,0),∴ ∴二次函数的表达式为 (2)∵点D(2,m)在抛物线上,即 ∴点D的坐标为(2,-4). 如解图①,过点E作EF⊥PB于点F,设点P坐标为(t,0),其中 ∵PE∥AD, ∴△BEP ∽△BDA. ∴ ∴EF = ∴当t=1时, ∴此时点P的坐标为(1,0). (3) 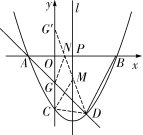 ∵A(-2,0),D(2,-4),∴直线AD的表达式为 ∵A(-2,0),D(2,-4),∴直线AD的表达式为∵当x=0时,y=-2, ∴点G的坐标为(0,-2), ∵当x=0时,二次函数的函数值y=-4, ∴点C的坐标为(0,-4), ∴点C,D关于直线x=1对称, 如解图,作点G关于x轴的对称点 ∴CG +GN +MN +MC =CG + ∵两点之间线段最短, ∴GN+NM+MC的最小值为 ∴四边形CMNG周长的最小值为2+ ∵D(2,-4), ∴直线D ∵当x=1时,y=-1;当y=0时, ∴满足条件的点M的坐标为(1,-1),点N的坐标为( (责任编辑:admin) |

 “引葭赴岸”是《九章算术》中的一道题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个边长为1O尺的正方形池塘,一棵芦苇
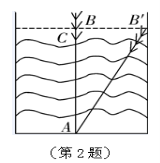
“引葭赴岸”是《九章算术》中的一道题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个边长为1O尺的正方形池塘,一棵芦苇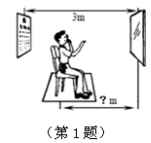 视力检测时要求被测的人与视力表的距离为5 m.如图所示,视力表与平面镜的距离是3 m.为满足测量要求,人与平面镜的距离应为 ()
视力检测时要求被测的人与视力表的距离为5 m.如图所示,视力表与平面镜的距离是3 m.为满足测量要求,人与平面镜的距离应为 ()