 
请点击全屏查看
2015年随州市中考数学模拟试卷
一、选择题(本大题共10个小题,每小题3分,共30分)
1、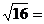 ( ) ( )
 A、4 B、±4 C、 A、4 B、±4 C、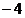 D、±8 D、±8
2、计算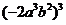
A、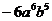 B、 B、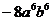 C、 C、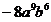 D、 D、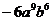
3、(2017随州数学)在平面直角坐标系xoy中,已知点P(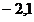 )与点Q(2, )与点Q(2,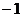 ),下列描述正确的序号是( ) ),下列描述正确的序号是( )
①关于x轴对称 ②关于y轴对称 ③关于原点对称 ④都在y=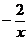 的图像上 的图像上
 A、①② B、②③ C、①④ D、③④ A、①② B、②③ C、①④ D、③④
4、如图,AB是⊙O的直径,C、D在圆上,
且∠BAC=28°,则∠ADC=( )
A、52° B、56° C、62° D、72°
5、在△ABC中,若AC:BC:AB=7:24:25,则sinA=( )
A、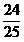 B、 B、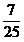 C、 C、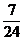 D、 D、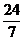
6.(2017随州数学)某商场一月份的营业额为400万元,第一季度营业总额为1600万元,若平均每月增长率为x,则可列方程为( )
| | A. | 400(1+x)2=1600 | B. | 400[1+(1+x)+ | (1+x)2]=1600 | | | | | | | | | C. | 400+400x+400x2=1600 | D. | 400(1+x+2x) | =1600 |
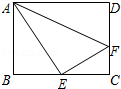
7.如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为( )
8.(2017随州数学)如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1+1,2a2+1,…,2an+1的方差是( )
9.已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:
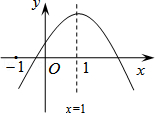 ①ac>0; ①ac>0;
②a﹣b+c<0;
③当x<0时,y<0;
④方程ax2+bx+c=0(a≠0)有两个
大于﹣1的实数根.
其中错误的结论有( )
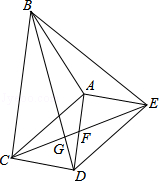 10.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于G,连结BE.下列结论中: 10.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于G,连结BE.下列结论中:
①CE=BD=2;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④CD•AE=EF• CG. CG.
一定正确的是( )
二(2017随州数学)、填空题:(本大题共6小题,每小题3分,共18分)
 11.不等式: 11.不等式: 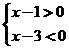 的解集是_____ 的解集是_____ ____________. ____________.
12、在实数范围内分解因式 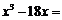 . .
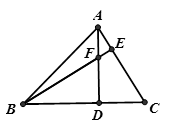
13、如图,△ABC中,A D⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么 D⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么
∠ABC的大小是 .
14.在Rt△ABC中,∠C=90°,AC=3,BC=4,将△ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的表面积 是 _________ . 是 _________ .
 15.反比例函数 15.反比例函数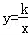 的图象经过点P(a,b),其中a、b是一元二次方程x2+kx+4=0的两根,那么点P的坐标是 _________ . 的图象经过点P(a,b),其中a、b是一元二次方程x2+kx+4=0的两根,那么点P的坐标是 _________ .
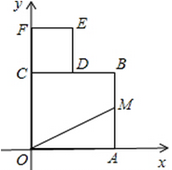
16.(2017随州数学)如图,在平面直角坐标系中,四边形OABC与CDEF都是正方形,OA=2,M、D分别是AB、BC的中点,当把正方形CDEF绕点C旋转某个角度或沿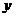 轴上下平移后,若点F的对应点为F′, 轴上下平移后,若点F的对应点为F′,
且O F′=OM,则点F′的坐标是___________________
三、(2017随州数学)解答题:(本大题共9小题,共72分)
17.(4分)先化简,再求值;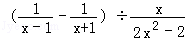 ,其中x=tan60°﹣1. ,其中x=tan60°﹣1.
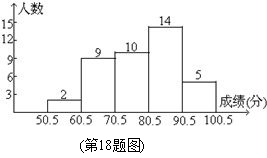 18. (6分)初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题: 18. (6分)初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:
(1)该班共有_______________名同学参加这次测验;
(2)这次测验成绩的中位数落在_____________分数段内;
(3)若这次测验中,成绩80分以上(不含80分)为优秀, 那么该班这次数学测验的优秀率是多少?
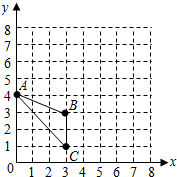
19.(7分)已知△ABC在平面直角坐标系中的位置如图所示.
(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)求点A旋转到点A′所经过的路线长(结果保留π).
.
20.(2017随州数学)(9分)已知x1、x2是一元二次方程2x2﹣2x+m+1=0的两个实数根.
(1)求实数m的取值范围;
(2)如果x1、x2满足不等式7+4x1x2>x12+x22,且m为负整数,求出m的值,并解出方程的根.
(友情提示:若一元二次方程ax2+bx+c=0有两根x1、x2,则x1+x2=﹣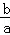 ,x1•x2= ,x1•x2=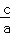 ) )
21、(8分)为执行“节能减排,美化环境,建设美丽新农村”的国策,某村计划建造A、B两种型号的沼气池共 20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表: 20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
| 型 号 | 占 地 面 积(m2/个) | 使 用 农 户 数(户/个) | 造 价(万元/个) | | A | 15 | 18 | 2 | | B | 20 | 30 | 3 |
已知可供建造沼气池的占地面积不超过365 m2,该村农户共有492户. m2,该村农户共有492户.
(1)满足条件的方案有哪几种?写出解答过程.
(2)通过计算判断,那种方案最省钱?
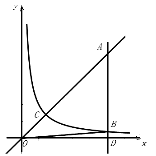 22、(2017随州数学)(10分)如图,B为双曲线 22、(2017随州数学)(10分)如图,B为双曲线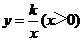 上一点,直线AB平行于y轴交直线 上一点,直线AB平行于y轴交直线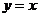 于点A,交x轴于点D, 于点A,交x轴于点D,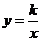 与直线 与直线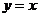 交于点C,若 交于点C,若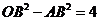
(1)求k的值;
(2)点B的横坐标为4时,求△ABC的面积;
(3)双曲线上是否存在点B,使△ABC∽△AOD?若存
在,求出点B的坐标;若不存在,请说明理由.
23、(7分)“健行”保健器械厂在某社区举办“品牌跑步机 团购销售”活动,销售规则如 团购销售”活动,销售规则如 下:若团购台数在30台或30台以下,跑步机每台售价900元;若团购台数多于30台,则给予优惠,每多1台,跑步机每台少10元,但团购台数最多为75台,已知器械厂举办该次活动须支付各项 下:若团购台数在30台或30台以下,跑步机每台售价900元;若团购台数多于30台,则给予优惠,每多1台,跑步机每台少10元,但团购台数最多为75台,已知器械厂举办该次活动须支付各项 成本15000元. 那么当团购台数为多少时,器械厂可获得的利润最大?是多少元? 成本15000元. 那么当团购台数为多少时,器械厂可获得的利润最大?是多少元?
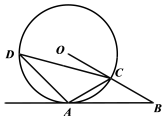 24、(8分)已知,A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC= 24、(8分)已知,A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC=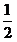 OB. OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
25、(2017随州数学)(13分)如图,平面直角坐标系xoy中,A(0,12),B(40,0),C(36,12),点P从点A出发,以1个单位/s的速度向点C运动;点Q从B同时出发,以2个单位/s的速度 向点O运动,规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为ts. 向点O运动,规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为ts.
(1)求过O,C,B三点的抛物线解析式;
(2)t为何值时,PQ=BC;
(3)在(1)中的抛物线上,是否存在点M,使以O,M,P,Q为顶点的四边形为平行四边形?若存在,直接写出 此时t的值和M点的坐标;若不存在,请说明理由 . 此时t的值和M点的坐标;若不存在,请说明理由 .
数学参考答案
一、选择题(本大题共10个小题,每小题3分,共30分)
1—10 ACDCA BDCAC
二、填空题:(本大题共6小题,每小题3分,共18分)
11、 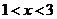 ; 12. ; 12. 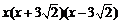
13. 45° 14、36π
15、P的坐标是(﹣2,﹣2).
16、(2017随州数学)(0,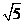 )或(0,- )或(0,-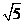 )或(-1,2)或(1,2). )或(-1,2)或(1,2).
三、解答题:(本大题共9小题,共72分)
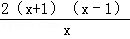 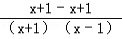

17、(4分)原式 =• =
当x=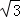 ﹣1时,原式 = ﹣1时,原式 =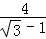 =2( =2(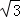 +1)=2 +1)=2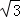 +2. +2.
18.(6分)(1)参加这次测验的人数有2+9+10+14+5=40人
(2)中位数就是第20,21的成 绩的和的一 绩的和的一 半, 半,
所以从表中可知2+9+10=21,
所以中位数落在70.5~80.5这一分数段.
(3) 优秀率= 优秀率=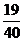 =47.5%. =47.5%.
19(2017随州数学)、(7分)
(1)A(0,4)、C(3,1);(2分)
(2)图略;(2分)
(3)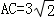
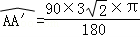
=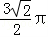 .(3分) .(3分)
20、(2017随州数学)(9 分)解:(1)根据题意得△=(﹣2)2﹣4×2×(m﹣1)≥0, 分)解:(1)根据题意得△=(﹣2)2﹣4×2×(m﹣1)≥0,
解得m≤﹣ ;(3分) ;(3分)
(2)根据题意得x1+x2=1,x1•x2=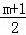 , ,
∵7+4x1x2>x12+x22,
∴7+6x1•x2>(x1+x2)2,
∴7+6×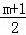 >1,解得m>﹣3, >1,解得m>﹣3,
∴﹣3<m≤﹣ , ,
∵m为负整数,
∴m=﹣2或m=﹣1,
当m=﹣2时,方程变形为2x2﹣2x﹣1=0,
解得x1=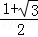 ,x2= ,x2=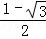 ; ;
当m=﹣1时,方程变形为x2﹣x=0,
解得x1=1,x2=0.(6分)
21.(2017随州数学) (8分) 设建造A型沼气池x个,建造B型沼气池y个,
则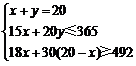 ,解得7≤x≤ ,解得7≤x≤ 9, 9,
又x为整数,∴x可取7,8,9. 相应的y取13,12,11.
造价对应为53,52,51.
故满足条件的方案有三种,
其中A型建9个,B型建11个时,造价最低,费用为51万元.
22. (10分)(1)k=2; (3分)
(2)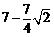 (3分) (3分)
(3)不存在,
提示:假设存在,过C作CM⊥AB于M,∵△OAD为等腰直角三角形,
∴△ACB也为等腰直角三角形. ∴CM=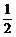 AD, AD,
设B(a, 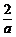 ). 则A(a, a),CM= ). 则A(a, a),CM=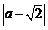 . ∴ . ∴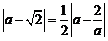 , 解得 , 解得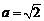 . .
此时C与B重合,不构成三角形,故不存在. (4分)
23. (7分)设团购台数为x台时,器械厂获得的利润为W元,则
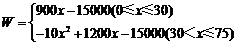
当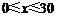 时, 时,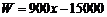 ,当x=30时,W最大=12000元. ,当x=30时,W最大=12000元.
当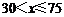 时, 时,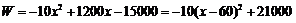 , ,
∴当x=60时,W最大=21000元.
∵21000>12000,∴当团购台数为60台时,器械厂 可获得最大利润为21000元. 可获得最大利润为21000元.
24.(2017随州数学) (8分)(1)连结OA,由AC=OC=OB,得∠OAB=90°,
∴AB是⊙O的切线. (4分)
(2)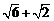 . .
提示:过A作AM⊥CD于M,
由题意可得∠ADC=30°. AC=OC=2,
则AM=MC=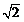 ,DM= ,DM=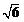 , ,
∴CD=DM+CM=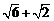 .(4分) .(4分)
25.(13分)(1)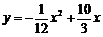 (3分) (3分)
(2)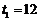 , ,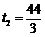 .(4分) .(4分)
(3)存在,当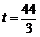 时,M(4,12); 时,M(4,12);
当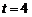 时,M(36,12); 时,M(36,12);
当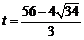 时,M( 时,M(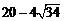 ,-12)(6分) ,-12)(6分)
(责任编辑:admin) |