|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看 2018年临汾中考数学复习题 一、选择题       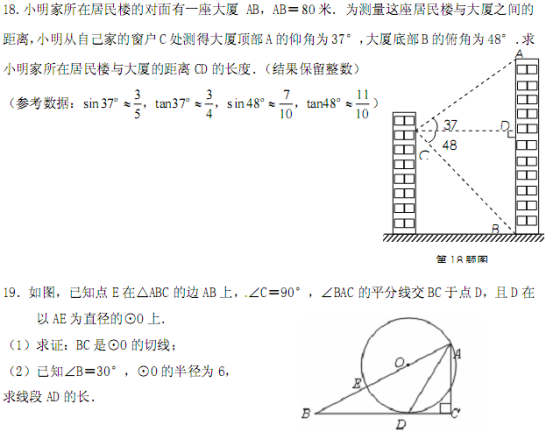  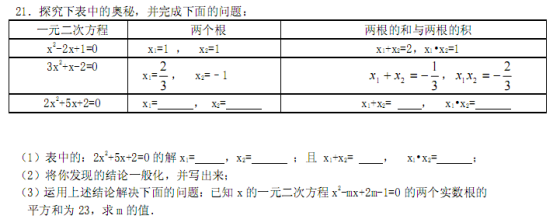       2018年临汾中考数学复习题 1—5：ACDBC 6：  7：6、6.5 8：11 9： 10： 、 11：解：原式=  = 12：解：原方程化为：  方程两边同乘以 得：   经检验：是原分式方程的解。∴原方程的解为。13：证明：∵∠1=∠2∴∠1+∠3=∠2+∠3(∠DAC记为∠3) ∴∠BAC=∠DAE 在△BAC=△DAE中   ∴△BAC≌△DAE ∴BC=DE14： (1) （2）AB=   （3） 15：解⑴把B（2，-4）代入  得：  ∴反比例函数的解析式为 把A（-4，  ）代入得： ∴点A的坐标为（-4，2） 把A（-4，2）和B（2，-4）代入 得： 解得： ∴一次函数的解析式为 ⑵由图象可得：方程  的解是  ⑶由图象可得：不等式 的解集是 或 16：解：⑴随机地抽取一张，P(偶数)=  = 能组成：12，13，14，21，23，24， 31，32，34，41，42，43 ⑵根据树形图可得：P(恰好为“24”)=   17：解：⑴如图所示，与墙面垂直的一边长为 米，则与墙面平行的一边长为 米，则：   由  得： 所以，与的函数关系式是  ，自变量 的取值范围是⑵  ，  当  时， ∵  ∴当 时， 有最大值 ∴生物园的面积不能达到120平方米。  注：第⑵问也可以得到方程 ，化简得 ，然后计算得到：△<0，方程无解，从而得到“生物园的面积不能达到120平方米”的答案。18：解：设CD= 米，则： ， 即： ， 则：  解得：  答：小明家所在居民楼与大厦的距离CD的长度约是43米。 19：解：⑴连接OD∵AD平分∠BAC ∴∠1=∠2(∠BAD记为∠1，∠DAC记为∠2，∠ODA记为∠3) ∵OD=OA∴∠1=∠3 ∴∠2=∠3∴OD∥AC  ∵∠C=90°∴∠ODC=90° ∴BC是⊙O的切线⑵（2）解：连接DE．∵∠B=30°，∴∠BAC=60°，即∠1=30°， ∵AE为⊙O的直径，∴∠ADE=90°，∵OA=6，∴AE=12， ∴cos∠1=  ，∴AD=AE•cos∠1=AE•cos30°=12× = ． 20、（1）解：∵△ABC是等边三角形，且D是BC中点，∴DA平分∠BAC，即∠DAB=∠DAC=30°； ∵△DAE是等边三角形，∴∠DAE=60°； ∴∠CAE=∠DAE-∠CAD=30°； （2）证明：∵△BAC是等边三角形，F是AB中点，∴CF⊥AB； 由（1）知：∠CAE=30°，∠BAC=60°；∴∠FAE=90°；∴AE∥CF； ∵△BAC是等边三角形，且AD、CF分别是BC、AB边的中线， ∴AD=CF；又AD=AE，∴CF=AE；∴四边形AFCE是平行四边形； ∵∠AFC=∠FAE=90°，∴四边形AFCE是矩形． 21解：（1）  （2）设  且a，b，c是常数）的两个实数根为 ， ．则  （3）设方程  的两个实数根为 、 ，由（2）可知 ∵  即 ∴  解得： ∵当  时，原方程无实数解，应舍去．∴当  时，方程的两个实数根的平方和为23．22、解：（1）∵点A在线段PQ的垂直平分线上，∴AP = AQ. ∵∠DEF = 45°，∠ACB = 90°，∠DEF＋∠ACB＋∠EQC = 180°， ∴∠EQC = 45°.∴∠DEF =∠EQC.∴CE = CQ. 由题意知：CE = t，BP =2 t， ∴CQ = t.∴AQ = 8－t. 在Rt△ABC中，由勾股定理得：AB = 10 cm .则AP = 10－2 t. ∴10－2 t = 8－t. 解得：t = 2. 答：当t = 2 s时，点A在线段PQ的垂直平分线上. 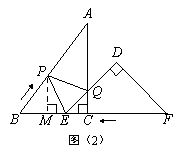 （2）过P作 ，交BE于M，∴  .在Rt△ABC和Rt△BPM中，  ，∴  . ∴PM =  .∵BC = 6 cm，CE = t， ∴ BE = 6－t. ∴y = S△ABC－S△BPE =  － =  － =  =  .∵  ，∴抛物线开口向上.∴当t = 3时，y最小=  .答：当t = 3s时，四边形APEC的面积最小，最小面积为 cm2.23、解：（1）    △ △    作   ，    （2）要使    在Rt△ 即： ， 即：当  （3）假设存在某一时刻  ， 分菱形上、下两部分的面积之比为3：7则       解得  分菱形上、下两部分的面积之比为3：7 24、1 (责任编辑：admin) |