|
☆☆☆ 点击下载试题 ☆☆☆ 请点击全屏查看 2016抚顺市抚顺县九年级期末数学试卷 一、选择题（每小题3分，共30分） 1．下列车标图案中，是中心对称图形的是（ ） A．  B． C． D． 2．一元二次方程x2=x的根是（ ） A．x=1 B．x=0 C．x1=x2 D．x1=0，x2=1 3．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（ ） A．开口向下 B．对称轴是x=﹣1 C．顶点坐标是（1，2） D．与x轴有两个交点 4．（2016抚顺数学）一儿童行走在如图所示的地板上，当他随意停下时，最终停在地板上阴影部分的概率是（ ）  A．  B． C． D． 5．某商品经过两次连续降价，每件售价由原来的100元降到了64元．设平均每次降价的百分率为x，则下列方程中正确的是（ ） A．100（1+x）2=64 B．64（1+x）2=100 C．64（1﹣x）2=100 D．100（1﹣x）2=64 6．将抛物线y=x2沿y轴向上平移一个单位后得到的新抛物线的解析式为（ ） A．y=（x+1）2 B．y=（x﹣1）2 C．y=x2+1 D．y=x2﹣1 7．已知抛物线y=x2﹣x﹣2与x轴的一个交点为（m，0），则代数式m2﹣m+2016的值为（ ） A．2015 B．2016 C．2017 D．2018 8．半径为R的圆内接正六边形的面积是（ ） A．R2 B．  R2 C． R2 D． R29．（2016抚顺数学）75°的圆心角所对的弧长是2.5πcm，则此弧所在圆的半径是（ ） A．6cm B．7cm C．8cm D．9cm 10．如图，在△ABC中，∠C=90°，∠BAC=70°，将△ABC绕点A顺时针旋转70°，B、C旋转后的对应点分别是B′和C′，连接BB′，则∠BB′C′的度数是（ ）  A．35° B．40° C．45° D．50° 二、填空题（每小题3分，共24分） 11．方程x2=  x的根是______．12．（2016抚顺数学）二次函数y=  （x﹣1）2﹣2的顶点坐标是______．13．已知3是一元二次方程x2﹣4x+c=0的一个根，则方程的另一个根是______． 14．如图，⊙O的直径CD=10，AB是⊙O的弦，AB⊥CD于M，且CM=2，则AB的长为______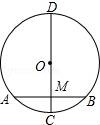．  15．已知二次函数y=x2+bx+c的图象如图所示，则关于x的方程x2+bx+c=0的解为x1=______，x2=3．  16（2016抚顺数学）．如图，两圆圆心相同，大圆的弦AB与小圆相切，AB=8，则图中阴影部分的面积是______．（结果保留π）  17．如图，有四张卡片（形状、大小和质地都相同），正面分别写有字母A、B、C、D和一个不同的算式，将这四张卡片背面向上洗匀，从中随机抽取两张卡片，这两张卡片上的算式只有一个正确的概率是______．  18．如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，那么DH的长是______．  三、（2016抚顺数学）解答题（第19题12分，第20题10分，共计22分） 19．解方程： （1）x2﹣8x+1=0（配方法） （2）（2x+1）2﹣4x﹣2=0． 20．如图，将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′． （1）画出旋转后的四边形A′B′C′D′； （2）写出A′、B′、C′、D′的坐标； （3）若每个小正方形的边长是1，请直接写出四边形ABCD的面积．  四、（2016抚顺数学）解答题 21．如图所示，在梯形ABCD中，AB∥CD，⊙O为内切圆，E、F为切点． （1）试猜DO与AO的位置关系，并说明理由． （2）若AO=4cm，DO=3cm，求⊙O的面积．  五、解答题（第22题12分，第23题12分，共计24分） 22．如图是二次函数y=a（x+1）2+2的图象的一部分，根据图象回答下列问题． （1）抛物线与x轴的一个交点的坐标是______，则抛物线与x轴的另一个交点B的坐标是______； （2）确定a的值； （3）设抛物线的顶点是P，试求△PAB的面积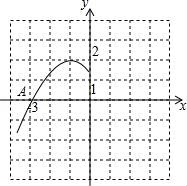．  23．（2016抚顺数学）兴隆镇某养鸡专业户准备建造如图所示的矩形养鸡场，要求长与宽的比为2：1，在养鸡场内，沿前侧内墙保留3m宽的走道，其他三侧内墙各保留1m宽的走道，当矩形养鸡场长和宽各为多少时，鸡笼区域面积是288m2？  六、解答题 24．一个不透明的口袋中装有4个分别标有数1，2，3，4的小球，它们的形状、大小完全相同，小红先从口袋里随机摸出一个小球记下数为x，小颖在剩下的3个球中随机摸出一个小球记下数为y，这样确定了点P的坐标（x，y）． （1）小红摸出标有数3的小球的概率是______． （2）请你用列表法或画树状图法表示出由x，y确定的点P（x，y）所有可能的结果． （3）求点P（x，y）在函数y=﹣x+5图象上的概率． 七、解答题 25．（2016抚顺数学）如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°． （1）求证：AC是⊙O的切线； （2）求弦BD的长； （3）求图中阴影部分的面积．  八、解答题 26．如图，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，B（3，5），抛物线y=﹣  x2+bx+c交x轴于点C，D两点，且经过点B．（1）（2016抚顺数学）求抛物线的表达式； （2）在抛物线上是否存在点F，使得△ACF的面积等于5，若存在，求出点F的坐标；若不存在，说明理由； （3）点M（4，k）在抛物线上，连接CM，求出在坐标轴的点P，使得△PCM是以∠PCM为顶角以CM为腰的等腰三角形，请直接写出P点的坐标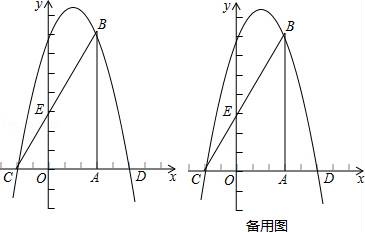．  2016抚顺数学参考答案与试题解析 一、选择题（每小题3分，共30分） 1．下列车标图案中，是中心对称图形的是（ ） A．  B． C． D． 【考点】中心对称图形． 【分析】根据中心对称图形的概念求解即可． 【解答】解：A、不是中心对称图形，本选项错误； B、不是中心对称图形，本选项错误； C、是中心对称图形，本选项正确； D、不是中心对称图形，本选项错误． 故选C． 2．（2016抚顺数学）一元二次方程x2=x的根是（ ） A．x=1 B．x=0 C．x1=x2 D．x1=0，x2=1 【考点】解一元二次方程-因式分解法． 【分析】移项后左边因式分解即可得． 【解答】解：x2﹣x=0， x（x﹣1）=0， ∴x1=0，x2=1， 故选：D． 3．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（ ） A．开口向下 B．对称轴是x=﹣1 C．顶点坐标是（1，2） D．与x轴有两个交点 【考点】二次函数的性质． 【分析】根据抛物线的性质由a=1得到图象开口向上，根据顶点式得到顶点坐标为（1，2），对称轴为直线x=1，从而可判断抛物线与x轴没有公共点． 【解答】解：二次函数y=（x﹣1）2+2的图象开口向上，顶点坐标为（1，2），对称轴为直线x=1，抛物线与x轴没有公共点． 故选：C． 4．（2016抚顺数学）一儿童行走在如图所示的地板上，当他随意停下时，最终停在地板上阴影部分的概率是（ ）  A．  B． C． D． 【考点】几何概率． 【分析】根据几何概率的求法：最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值． 【解答】解：观察这个图可知：黑色区域（3块）的面积占总面积（9块）的 ，故其概率为 ．故选：A． 5．（2016抚顺数学）某商品经过两次连续降价，每件售价由原来的100元降到了64元．设平均每次降价的百分率为x，则下列方程中正确的是（ ） A．100（1+x）2=64 B．64（1+x）2=100 C．64（1﹣x）2=100 D．100（1﹣x）2=64 【考点】由实际问题抽象出一元二次方程． 【分析】设平均每次降价的百分率为x，则等量关系为：原价×（1﹣x）2=现价，据此列方程． 【解答】解：设平均每次降价的百分率为x， 由题意得，100×（1﹣x）2=64 故选D． 6．将抛物线y=x2沿y轴向上平移一个单位后得到的新抛物线的解析式为（ ） A．y=（x+1）2 B．y=（x﹣1）2 C．y=x2+1 D．y=x2﹣1 【考点】二次函数图象与几何变换． 【分析】直接根据平移规律作答即可． 【解答】解：将抛物线y=x2沿y轴向上平移一个单位后得到的新抛物线的解析式为y=x2+1， 故选C． 7．已知抛物线y=x2﹣x﹣2与x轴的一个交点为（m，0），则代数式m2﹣m+2016的值为（ ） A．2015 B．2016 C．2017 D．2018 【考点】抛物线与x轴的交点． 【分析】直接利用抛物线上点的坐标性质进而得出m2﹣m=2，即可得出答案． 【解答】解：∵抛物线y=x2﹣x﹣2与x轴的一个交点为（m，0）， ∴m2﹣m﹣2=0， ∴m2﹣m=2， ∴m2﹣m+2016=2+2016=2018． 故选：D． 8．（2016抚顺数学）半径为R的圆内接正六边形的面积是（ ） A．R2 B．  R2 C． R2 D． R2【考点】正多边形和圆． 【分析】利用正六边形的特点，它被半径分成六个全等的等边三角形． 【解答】解：连接正六边形的中心与各个顶点，得到六个等边三角形，等边三角形的边长是R， 因而面积是  = ，因而正六边形的面积是6× =R2．故选：C． 9．（2016抚顺数学）75°的圆心角所对的弧长是2.5πcm，则此弧所在圆的半径是（ ） A．6cm B．7cm C．8cm D．9cm 【考点】弧长的计算． 【分析】根据弧长公式L=  ，将n=75，L=2.5π，代入即可求得半径长．【解答】解：∵75°的圆心角所对的弧长是2.5πcm， 由L= ，∴2.5π=  ，解得：r=6， 故选：A． 10．如图，在△ABC中，∠C=90°，∠BAC=70°，将△ABC绕点A顺时针旋转70°，B、C旋转后的对应点分别是B′和C′，连接BB′，则∠BB′C′的度数是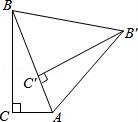（ ）  A．35° B．40° C．45° D．50° 【考点】旋转的性质． 【分析】首先在△ABB'中根据等边对等角，以及三角形内角和定理求得∠ABB'的度数，然后在直角△BB'C中利用三角形内角和定理求解． 【解答】解：∵AB=AB'， ∴∠ABB'=∠AB'B=  = =55°，在直角△BB'C中，∠BB'C=90°﹣55°=35°． 故选A． 二、（2016抚顺数学）填空题（每小题3分，共24分） 11．方程x2=  x的根是 x1=0，x2= ．【考点】解一元二次方程-因式分解法． 【分析】方程整理后，利用因式分解法求出解即可． 【解答】解：方程整理得：x（x﹣ ）=0，可得x=0或x﹣ =0，解得：x1=0，x2= ．故答案为：x1=0，x2= 12．二次函数y= （x﹣1）2﹣2的顶点坐标是 （1，﹣2） ．【考点】二次函数的性质． 【分析】直接根据顶点式的特点写出顶点坐标． 【解答】（2016抚顺数学）解：二次函数y= （x﹣1）2﹣2的顶点坐标是：（1，﹣2）．故答案为：（ 1，﹣2）． 13．已知3是一元二次方程x2﹣4x+c=0的一个根，则方程的另一个根是 1 ． 【考点】根与系数的关系． 【分析】设另一个根为t，根据根与系数的关系得到3+t=4，然后解一次方程即可． 【解答】解：设另一个根为t， 根据题意得3+t=4， 解得t=1， 则方程的另一个根为1． 故答案为：1． 14．如图，⊙O的直径CD=10，AB是⊙O的弦，AB⊥CD于M，且CM=2，则AB的长为 8 ．  【考点】垂径定理；勾股定理． 【分析】连接OA，求得OA和OM的长，在直角△OAM中利用勾股定理求得AM的长，然后根据AB=2AM即可求解． 【解答】（2016抚顺数学）解：连接OA．则OA=OC= CD=5．则OM=OC﹣CM=5﹣3=3． 在直角△OAM中，AM=  = =4．∵AB⊥CD于M， ∴AB=2AM=8． 故答案是：8．  15．已知二次函数y=x2+bx+c的图象如图所示，则关于x的方程x2+bx+c=0的解为x1= ﹣1 ，x2=3．  【考点】（2016抚顺数学）抛物线与x轴的交点． 【分析】抛物线与x轴的交点的横坐标就是x的值． 【解答】解：关于x的方程x2+bx+c=0的解为x1=﹣1，x2=3． 故答案是：﹣1． 16．如图，两圆圆心相同，大圆的弦AB与小圆相切，AB=8，则图中阴影部分的面积是 16π ．（结果保留π）  【考点】（2016抚顺数学）切线的性质；勾股定理；垂径定理． 【分析】设AB与小圆切于点C，连结OC，OB，利用垂径定理即可求得BC的长，根据圆环（阴影）的面积=π•OB2﹣π•OC2=π（OB2﹣OC2），以及勾股定理即可求解． 【解答】解：设AB与小圆切于点C，连结OC，OB． ∵AB与小圆切于点C， ∴OC⊥AB， ∴BC=AC= AB=×8=4．∵圆环（阴影）的面积=π•OB2﹣π•OC2=π（OB2﹣OC2） 又∵直角△OBC中，OB2=OC2+BC2 ∴圆环（阴影）的面积=π•OB2﹣π•OC2=π（OB2﹣OC2）=π•BC2=16π． 故答案为：16π．  17．（2016抚顺数学）如图，有四张卡片（形状、大小和质地都相同），正面分别写有字母A、B、C、D和一个不同的算式，将这四张卡片背面向上洗匀，从中随机抽取两张卡片，这两张卡片上的算式只有一个正确的概率是  ． 【考点】列表法与树状图法． 【分析】首先此题需要两步完成，直接运用树状图法或者采用列表法，再根据列举求出所用可能数，再求出只有一次正确的情况数根据概率公式解答即可． 【解答】解：列表如下：
由表可知一共有12种情况，其中抽取的两张卡片上的算式只有一个正确的有8种， 所以两张卡片上的算式只有一个正确的概率=  ，故答案为： ．18．（2016抚顺数学）如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，那么DH的长是  ． 【考点】正方形的性质；旋转的性质；解直角三角形． 【分析】连接CH，可知△CFH≌△CDH（HL），故可求∠DCH的度数；根据三角函数定义求解． 【解答】（2016抚顺数学）解：连接CH． ∵四边形ABCD，四边形EFCG都是正方形，且正方形ABCD绕点C旋转后得到正方形EFCG， ∴∠F=∠D=90°， ∴△CFH与△CDH都是直角三角形， 在Rt△CFH与Rt△CDH中， ∵  ，∴△CFH≌△CDH（HL）． ∴∠DCH= ∠DCF=（90°﹣30°）=30°．在Rt△CDH中，CD=3， ∴DH=tan∠DCH×CD= ．故答案为： ． 三、（2016抚顺数学）解答题（第19题12分，第20题10分，共计22分） 19．解方程： （1）x2﹣8x+1=0（配方法） （2）（2x+1）2﹣4x﹣2=0． 【考点】解一元二次方程-因式分解法；解一元二次方程-配方法． 【分析】（1）先利用配方法得到（x﹣4）2=15，然后利用直接开平方法解方程； （2）先变形为（2x+1）2﹣2（2x+1）=0，然后利用因式分解法解方程． 【解答】解：（1）移项得 x2﹣8x=﹣1， 配方得 x2﹣8x+42=﹣1+42， （x﹣4）2=15， x﹣4=±  ，即x1=4+ x2=4﹣；（2）（2x+1）2﹣2（2x+1）=0， （2x+1）（2x﹣1）=0， 2x+1=0或2x﹣1=0 所以解得x1=﹣  x2=．20．（2016抚顺数学）如图，将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′． （1）画出旋转后的四边形A′B′C′D′； （2）写出A′、B′、C′、D′的坐标； （3）若每个小正方形的边长是1，请直接写出四边形ABCD的面积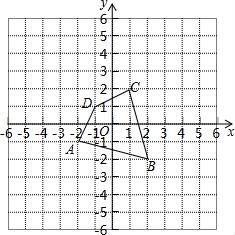．  【考点】作图-旋转变换． 【分析】（1）根据网格结构找出点A、B、C、D关于原点对称的点A′、B′、C′、D′的位置，然后顺次连接即可； （2）根据平面直角坐标系写出各点的坐标即可； （3）利用四边形所在的矩形的面积减去四周四个小直角三角形和一个小正方形的面积，列式计算即可得解． 【解答】（2016抚顺数学）解：（1）四边形A′B′C′D′如图所示； （2）A′（2，1）、B′（﹣2，2）、C′（﹣1，﹣2）、D′（1，﹣1）； （3）S四边形ABCD=4×4﹣ ×1×4﹣×1×4﹣×1×2﹣×1×2﹣1×1，=16﹣2﹣2﹣1﹣1﹣1， =16﹣7， =9．  四、解答题 21．如图所示，在梯形ABCD中，AB∥CD，⊙O为内切圆，E、F为切点． （1）试猜DO与AO的位置关系，并说明理由． （2）若AO=4cm，DO=3cm，求⊙O的面积． 【考点】（2016抚顺数学）切线的性质；梯形． 【分析】（1）由⊙O是梯形ABCD的内切圆，易得DE和DF是⊙O的两条切线，即可得∠ADO+∠DAO= （∠ADC+∠DAB），又由AB∥CD，可得∠ADO+∠DAO=90°，继而证得结论；（2）由AO=4cm，DO=3cm，可求得AD的长，继而求得EO的长，则可求得答案． 【解答】解：（1）AO⊥DO． 理由：∵⊙O是梯形ABCD的内切圆， ∴DE和DF是⊙O的两条切线， ∴∠ADO=∠CDO= ∠ADC．同理可得：∠DAO= ∠DAB．∴∠ADO+∠DAO= （∠ADC+∠DAB），∵AB∥CD， ∴∠ADC+∠DAB=180°， ∴∠ADO+∠DAO= ×180°=90°，∵∠AOD=180°﹣（∠ADO+∠DAO）=90°， ∴AO⊥DO； （2）∵DO=3cm AO=4cm，∠AOD=90° ∴AD=  =5 cm，在Rt△AOD中，EO⊥AD， ∴AD•EO=DO•AO， 即5 EO=3×4， 解得EO=  cm，∴S⊙O=πEO2=π （ ）2= π．五、（2016抚顺数学）解答题（第22题12分，第23题12分，共计24分） 22．如图是二次函数y=a（x+1）2+2的图象的一部分，根据图象回答下列问题． （1）抛物线与x轴的一个交点的坐标是 （﹣3，0） ，则抛物线与x轴的另一个交点B的坐标是 （1，0） ； （2）确定a的值； （3）设抛物线的顶点是P，试求△PAB的面积．  【考点】抛物线与x轴的交点． 【分析】（1）由图象可求得A点的坐标，由解析式可求得抛物线的对称轴方程，利用图象的对称性可求得B点坐标； （2）把B点坐标代入抛物线解析式可求得a的值； （3）由抛物线解析式可求得P点坐标，再结合A、B坐标可求得AB的值，则可求得△PAB的面积． 【解答】（2016抚顺数学）解： （1）由图象可知A点坐标为（﹣3，0）， ∵y=a（x+1）2+2， ∴抛物线对称轴方程为x=﹣1， ∵A、B两点关于对称轴对称， ∴B的坐标为（1，0）， 故答案为：（﹣3，0）；（1，0）； （2）将（1，0）代入y=a（x+1）2+2， 可得0=4a+2，解得a=﹣  ；（3）∵y=a（x+1）2+2， ∴抛物线的顶点坐标是（﹣1，2）， ∵A（﹣3，0），B（1，0）， ∴AB=XB﹣XA=1﹣（﹣3）=4， ∴S△PAB= ×4×2=4．23．兴隆镇某养鸡专业户准备建造如图所示的矩形养鸡场，要求长与宽的比为2：1，在养鸡场内，沿前侧内墙保留3m宽的走道，其他三侧内墙各保留1m宽的走道，当矩形养鸡场长和宽各为多少时，鸡笼区域面积是288m2？  【考点】一元二次方程的应用． 【分析】（2016抚顺数学）等量关系为：（鸡场的长﹣4）（鸡场的宽﹣2）=288，把相关数值代入求得合适的解即可． 【解答】解：设鸡场的宽为xm，则长为2xm． （2x﹣4）（x﹣2）=288， （x﹣14）（x+10）=0， 解得x=14，或x=﹣10（不合题意，舍去）． ∴2x=28． 答：鸡场的长为28m，宽为14m． 六、（2016抚顺数学）解答题 24．一个不透明的口袋中装有4个分别标有数1，2，3，4的小球，它们的形状、大小完全相同，小红先从口袋里随机摸出一个小球记下数为x，小颖在剩下的3个球中随机摸出一个小球记下数为y，这样确定了点P的坐标（x，y）． （1）小红摸出标有数3的小球的概率是  ．（2）请你用列表法或画树状图法表示出由x，y确定的点P（x，y）所有可能的结果． （3）求点P（x，y）在函数y=﹣x+5图象上的概率． 【考点】列表法与树状图法；一次函数图象上点的坐标特征． 【分析】（1）根据概率公式求解； （2）利用树状图展示所有12种等可能的结果数； （3）利用一次函数图象上点的坐标特征得到在函数y=﹣x+5的图象上的结果数，然后根据概率公式求解． 【解答】（2016抚顺数学）解：（1）小红摸出标有数3的小球的概率是 ；故答案为 ；（2）画树状图为：  由列表或画树状图可知，P点的坐标可能是（1，2）（1，3）（1，4）（2，1）（2，3）， （2，4）（3，1）（3，2）（3，4）（4，1）（4，2）（4，3）共12种情况， （3）共有12种可能的结果，其中在函数y=﹣x+5的图象上的有4种，即（1，4）（2，3）（3，2）（4，1） 所以点P（x，y）在函数y=﹣x+5图象上的概率=  = ．七、解答题 25．（2016抚顺数学）如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°． （1）求证：AC是⊙O的切线； （2）求弦BD的长； （3）求图中阴影部分的面积．  【考点】切线的判定；垂径定理的应用；扇形面积的计算． 【分析】（1）连接OC，OC交BD于E，由∠CDB=∠OBD可知，CD∥AB，又AC∥BD，四边形ABDC为平行四边形，则∠A=∠D=30°，由圆周角定理可知∠COB=2∠D=60°，由内角和定理可求∠OCA=90°，证明切线； （2）利用（1）中的切线的性质和垂径定理以及解直角三角形来求BD的长度； （3）证明△OEB≌△CED，将阴影部分面积问题转化为求扇形OBC的面积． 【解答】（1）证明：连接OC，OC交BD于E， ∵∠CDB=30°， ∴∠COB=2∠CDB=60°， ∵∠CDB=∠OBD， ∴CD∥AB， 又∵AC∥BD， ∴四边形ABDC为平行四边形， ∴∠A=∠D=30°， ∴∠OCA=180°﹣∠A﹣∠COB=90°，即OC⊥AC 又∵OC是⊙O的半径， ∴AC是⊙O的切线； （2）解：由（1）知，OC⊥AC． ∵AC∥BD， ∴OC⊥BD， ∴BE=DE， ∵在直角△BEO中，∠OBD=30°，OB=6， ∴BE=OBcos30°=3  ，∴BD=2BE=6 ；（3）解：易证△OEB≌△CED， ∴S阴影=S扇形BOC ∴S阴影=  =6π．答：阴影部分的面积是6π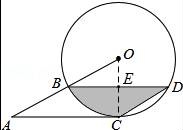．  八、（2016抚顺数学）解答题 26．如图，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，B（3，5），抛物线y=﹣ x2+bx+c交x轴于点C，D两点，且经过点B．（1）求抛物线的表达式； （2）在抛物线上是否存在点F，使得△ACF的面积等于5，若存在，求出点F的坐标；若不存在，说明理由； （3）点M（4，k）在抛物线上，连接CM，求出在坐标轴的点P，使得△PCM是以∠PCM为顶角以CM为腰的等腰三角形，请直接写出P点的坐标．  【考点】（2016抚顺数学）二次函数综合题． 【分析】（1）利用待定系数法求出抛物线解析式； （2）利用△ACF的面积等于5直接建立方程求出F点的纵坐标，代入抛物线解析式解方程即可； （3）先求出CM=3  ，再分点P在x轴和y轴上，用CM=CP求出点P的坐标．【解答】（1）∵B（3，5）， ∴OA=3，AB=5， ∵AB=AC， ∴OC=AC﹣OA=5﹣3=2， 即点C的坐标是（﹣2，0）， ∵点C（﹣2，0）和点B（3，5）在抛物线y=﹣  x2+bx+c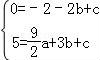上∴将其代入得  ，∴  ，∴抛物线的表达式是y=﹣ x2+ x+5，（2）（2016抚顺数学）假设抛物线上存在点F使得S△ACF=5，则设点F的坐标是（a，b） ∵ AC|b|=5，∴ ×5|b|=5，解得b=±2， 将F（a，2）和F（a，﹣2）分别代入y=﹣ x2+x+5中得﹣ a2+a+5=2，﹣a2+ a+5=﹣2解得a1=  a2= a3= a4= 所以符合条件的点F有四个，它们分别是F1（ ，2），F2（，2），F3（ ，﹣2）F4（ ，﹣2），（3）（2016抚顺数学）点M（4，k）在抛物线y=﹣ x2+ x+5的图象上，∴k=3， ∴M（4，3）， ∵C（﹣2，0）， ∴CM=3  ①当点P在x轴上时，设P（p，0）， ∴CP=|p+2|， ∵△PCM是以∠PCM为顶角以CM为腰的等腰三角形． ∴CM=CP， ∴|p+2|=3 ，∴p=﹣2±3 ，∴P1（﹣3 ﹣2，0）P2 （3 ﹣2，0），②当点P在y轴上时，设P（0，h）， ∴PC=  =3，∴h=±  ，∴P3（0， ） P4（0，﹣）．符合条件的P点有四个，它们分别是P1（﹣3 ﹣2，0）P2 （3﹣2，0），P3（0， ） P4（0，﹣）．第1页（共21页） (责任编辑：admin) |