|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看  2018年六盘水中考数学模拟试题一、选择题（本题有10个小题，每小题4分，共40分） 1、-4的倒数是（ ）A．4 B．-4 C．  D.－ 2、在▱ABCD中，点E为AD的中点，连接BE，交AC于点F，则AF：CF=（ ） A．1：2 B． 1：3 C． 2：3 D．2：5 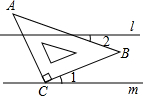 3、已知4个数据： ， ，a，b，其中a，b是方程 的两个根，则这4个数据的中位数是（ ） A．1 B．  C．2 D． 4、如图，直线l∥m，将含有45°角的三角板ABC的直角顶点C放 在直线m上，若∠1=25°，则∠2的度数为（ ） A．20° B．25° C．30° D．35° 5、两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视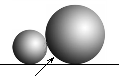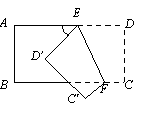（ ）    （A）两个外离的圆 （B）两个外切的圆（C）两个相交的圆 （D）两个内切的圆第7题图  第5题图 第8题图 6. 一组数据：10、5、15、5、20，则这组数据的平均数和中位数分别是（ ） A．10，10 B．10，12.5 C．11，12.5 D．11，10 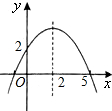 7、如图，抛物线y=ax2与反比例函数 的图象交于P点，若P点横坐标为1，则关于x的不等式 >0的解是（ ） A．x>1 B．x< -1 C．-1 8、如图所示 ，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′等于（ ） A． 70° B． 65° C． 50° D． 25° 9、二次函数y=ax2+bx+c（a≠0）的图象如图所示． 有下列结论：①b2-4ac＜0；②ab＞0；③a-b+c=0；④4a+b=0；⑤当y=2时，x只能等于0． 其中正确的是（ ）A．①④ B．③④ C．②⑤ D．③⑤ 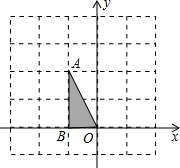 10. 如图，在平面直角坐标系中，Rt△OAB的三个顶点坐标分别是O（0，0），A（-1，2），B（-1，0）将△OAB先向左平移 1个单位长度得到△O′A′B′，再将△O′A′B′绕点O′按顺时针方向 旋转90°得到△O′A″B″，则点A″的坐标是（ ） A.（1，1） B.（-3，-1） C.（2，-2） D.（2，1） 二、填空题：（共10个小题，每题4分共40分） 11、分解因式：9a﹣ab2= ． 12、方程 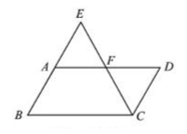 的解是 ．  13、一组样本数据4，0，2，-1，4，3的方差是 14、如图，□ABCD，E是BA延长线上一点，AB=AE，连接 CE交AD于点F，若CF平分∠BCD，AB=3，则BC的长为 ． 15、如图，上面各图都是用全等的等边三角形拼成的一组图形．则 在第10个这样的图形中共有 个等腰梯形． 16．在函数  中, 自变量 的取值范围是 .17．2015年“五一”期间约有359525人来黔东南旅游， 将数据359525用科学计数法(保留三个有效数字)表示为 . 18．某校举行以“保护环境，从我做起”为主题的演讲比赛．经预赛，七、八年级各有一名同学进入决赛，九年级有两名同学进入决赛．前两名都是九年级同学的概率是 . 19、如图，AB是⊙O的弦，OC是⊙O的半径，OC⊥AB于点D，AB＝16cm，OD＝6cm，那么⊙O的半径是______________ cm。 20、如图，学校有一块三角形空地（即△ABC），现准备将它分成面积相等的两块地，栽种不同的花草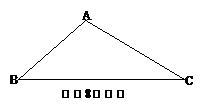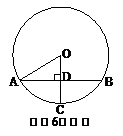，   请你把它分出来。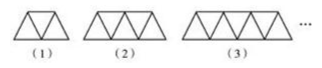（要求：尺规作图，保留作图痕迹，不写作法，不要求证明） （第15题） ![wps_clip_image-21239[4]](/uploads/collect/201905/11/114350.0294718.png) 三、解答题：（第19题每小题6分，共70分）21、（1）计算：  （2）解方程组：20、（1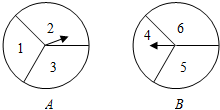0分）先化简  ，然后从不等组 的解集中，选取一个你认为符合题意的x的值代入求值． 21、（12分）有两个可以自由转动的均匀转盘A、B，都被分成了3等份，并在每份内均标有数字，如图所示，规则如下：①分别转动转盘A、B．②两个转盘停止后，将两个指针所指份内的数字相乘（若指针停在等分线上，那么重转一次，直到指针指向某一份为止）．（1）用列表法（或树状图）分别求出数字之积为3的倍数和为5的倍数的概率； （2）小亮和小芸想用这两个转盘做游戏，他们规定：数字之积为3的倍数时，小亮得2分；数字之积为5的倍数时，小芸得3分．这个游戏对双方公平吗？请说明理由；认为不公平的，试修改得分规定，使游戏双方公平． 21、（10分）凯里市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同. （1）甲、乙工程队每天各能铺设多少米？ （2）如果要求完成该项工程的工期不超过10天，那么为两工程队分配工程量（以百米为单位）的方案有几种？请你帮助设计出来. 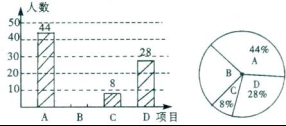 22、（12分）凯里市积极开展“阳光体育进校园”活动，各校学生坚持每天锻炼一小时．某校根据实际，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题．（1）样本中最喜欢B项目的人数百分比是____， 其所在扇形图中的圆心角的度数是____； （2）请把统计图补充完整； （3）已知该校有1200人，请根据样本估计全校 最喜欢乒乓球的人数是多少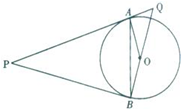？  23、（10分）如图所示，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O 上一点，且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．（1）求证：PB是⊙O的切线； （2）求证：AQ•PQ=OQ•BQ； （3）设∠AOQ=α，若cosα=  ，OQ=15，求AB的长．24、某工程机械厂根据市场需求，计划生产A、B两种型号的大型挖掘机共100台，该厂所筹生产资金不少于22 400万元，但不超过22 500万元，且所筹资金全部用于生产此两型挖掘机，所生产的此两型挖掘机可全部售出，此两型挖掘机的生产成本和售价如下表：
（1）该厂对这两型挖掘机有哪几种生产方案？ （2）该厂如何生产能获得最大利润？ （3）根据市场调查，每台B型挖掘机的售价不会改变，每台A型挖掘机的售价将会提高m万元（m＞0），该厂应该如何生产获得最大利润？（注：利润=售价-成本 25如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A，B两点，开口向下的抛物线经过点A，B，且其顶点P在⊙C上． （1）求∠ACB的大小； （2）写出A，B两点的坐标； （3）试确定此抛物线的解析式； （4）在该抛物线上是否存在一点D，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由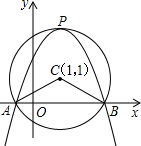．  (责任编辑：admin) |