|
☆☆☆ 点击下载试题 ☆☆☆ 请点击全屏查看 2017锦州市七中九年级第一次月考数学试卷 一、选择题（每小题3分，共18分） 1．已知关于x的一元二次方程x2﹣x+k=0的一个根是2，则k的值是（ ） A．﹣2 B．2 C．1 D．﹣1 2．下列性质中，矩形具有但菱形不一定具有的是（ ） A．对角线互相平分 B．对角线互相垂直 C．对角线相等 D．对边平行 3．下列各式是一元二次方程的是（ ） A．3﹣5x2=x B．  +x2﹣1=0 C．ax2+bx+c=0 D．4x﹣1=04．（2017锦州数学）顺次连接矩形各边中点所得的四边形是（ ） A．平行四边形 B．矩形 C．菱形 D．等腰梯形 5．要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ） A．  x（x+1）=28 B． x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=286．目前我国建立了比较完善的经济困难学生资助体系．某校去年上半年发放给每个经济困难学生389元，今年上半年发放了438元，设每半年发放的资助金额的平均增长率为x，则下面列出的方程中正确的是（ ） A．438（1+x）2=389 B．389（1+x）2=438 C．389（1+2x）2=438 D．438（1+2x）2=389 二、填空题（每小题3分，共18分） 7．（2017锦州数学）若关于x的一元二次方程kx2﹣6x+9=0有两个相等的实数根，则k= ． 8．（x1，y1）和（x2，y2）是双曲线y=﹣  上两点，当x1＜x2＜0时，y1与y2的大小关系是 ．9．如图所示，设A为反比例函数  图象上一点，且矩形ABOC的面积为3，则k= ． 10．如图，在菱形ABCD中，AC与BD相交于点O，AC=8，BD=6，则菱形的边长AB= ．  11．（2017锦州数学）如图，过矩形ABCD对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．若AB=  ，∠DCF=30°，则EF长为 ． 12．如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边作平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边作平行四边形AO1C2B；…；依此类推，则平行四边形AO4C5B的面积为 ．  三、（2017锦州数学）计算题：（每小题24分，共24分） 13．解方程 （1）（x﹣3）2=25（直开法） （2）x2+3x+2=0（十字相乘法） （3）x2﹣6x+8=0（配方法） （4）x2﹣x﹣1=0（公式法） 四、（2017锦州数学）解答题（17小题12分，18小题14分，19小题14分，共40分） 14．如图，在宽为20m，长为32m的矩形地上，修筑同样宽的三条道路，把耕地分成大小不等的六块，要使耕地面积为570m2，求道路的宽为多少米？  15．某水果批发商场经营一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要尽量减少库存，那么每千克应涨价多少元？ 16．如图，已知E是平行四边形ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F． （1）求证：△ABE≌△FCE； （2）连接AC、BF，若BC=2AE，求证：四边形ABFC为矩形； （3）在（2）条件下，当△ABC再满足一个什么条件时，四边形ABFC为正方形．（不需证明）  2017锦州数学参考答案与试题解析 一、（2017锦州数学）选择题（每小题3分，共18分） 1．已知关于x的一元二次方程x2﹣x+k=0的一个根是2，则k的值是（ ） A．﹣2 B．2 C．1 D．﹣1 【考点】一元二次方程的解． 【分析】知道方程的一根，把该根代入方程中，求出未知量k． 【解答】解：由题意知， 关于x的一元二次方程x2﹣x+k=0的一个根是2， 故4﹣2+k=0， 解得k=﹣2， 故选A． 2．（2017锦州数学）下列性质中，矩形具有但菱形不一定具有的是（ ） A．对角线互相平分 B．对角线互相垂直 C．对角线相等 D．对边平行 【考点】矩形的性质；菱形的性质． 【分析】根据矩形的对角线互相平分、相等和菱形的对角线互相平分、垂直、对角线平分一组对角，即可推出答案． 【解答】解：菱形的对角线互相平分、垂直、对角线平分一组对角，矩形的对角线互相平分、相等， 所以矩形具有而菱形不具有的性质是对角线相等， 故选C． 3．（2017锦州数学）下列各式是一元二次方程的是（ ） A．3﹣5x2=x B． +x2﹣1=0 C．ax2+bx+c=0 D．4x﹣1=0【考点】一元二次方程的定义． 【分析】本题根据一元二次方程的定义解答．一元二次方程必须满足四个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；（4）含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案． 【解答】解：A、符合一元二次方程的定义，正确； B、不是整式方程，故错误； C、方程二次项系数可能为0，故错误； D、方程未知数为1次，故错误； 故选A． 4．顺次连接矩形各边中点所得的四边形是（ ） A．平行四边形 B．矩形 C．菱形 D．等腰梯形 【考点】中点四边形． 【分析】（2017锦州数学）作出图形，根据三角形的中位线定理可得EF=GH=  AC，FG=EH=BD，再根据矩形的对角线相等可得AC=BD，从而得到四边形EFGH的四条边都相等，然后根据四条边都相等的四边形是菱形解答．【解答】解：如图，连接AC、BD， ∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点， ∴EF=GH= AC，FG=EH=BD（三角形的中位线等于第三边的一半），∵矩形ABCD的对角线AC=BD， ∴EF=GH=FG=EH， ∴四边形EFGH是菱形． 故选C．  5．（2017锦州数学）要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ） A． x（x+1）=28 B． x（x﹣1）=28 C．x（x+1）=28 D．x（x﹣1）=28【考点】由实际问题抽象出一元二次方程． 【分析】关系式为：球队总数×每支球队需赛的场数÷2=4×7，把相关数值代入即可． 【解答】解：每支球队都需要与其他球队赛（x﹣1）场，但2队之间只有1场比赛， 所以可列方程为： x（x﹣1）=4×7．故选：B． 6．（2017锦州数学）目前我国建立了比较完善的经济困难学生资助体系．某校去年上半年发放给每个经济困难学生389元，今年上半年发放了438元，设每半年发放的资助金额的平均增长率为x，则下面列出的方程中正确的是（ ） A．438（1+x）2=389 B．389（1+x）2=438 C．389（1+2x）2=438 D．438（1+2x）2=389 【考点】由实际问题抽象出一元二次方程． 【分析】先用含x的代数式表示去年下半年发放给每个经济困难学生的钱数，再表示出今年上半年发放的钱数，令其等于438即可列出方程． 【解答】解：设每半年发放的资助金额的平均增长率为x，则去年下半年发放给每个经济困难学生389（1+x）元，今年上半年发放给每个经济困难学生389（1+x）2元， 由题意，得：389（1+x）2=438． 故选B． 二、（2017锦州数学）填空题（每小题3分，共18分） 7．若关于x的一元二次方程kx2﹣6x+9=0有两个相等的实数根，则k= 1 ． 【考点】根的判别式． 【分析】由一元二次方程的定义可得出k≠0，根据方程有两个相等的实数根结合根的判别式即可得出关于k的一元一次方程，解之即可得出结论． 【解答】解：∵方程kx2﹣6x+9=0为一元二次方程， ∴k≠0． ∵关于x的一元二次方程kx2﹣6x+9=0有两个相等的实数根， ∴△=（﹣6）2﹣4×9k=36﹣36k=0， 解得：k=1． 故答案为：1． 8．（x1，y1）和（x2，y2）是双曲线y=﹣ 上两点，当x1＜x2＜0时，y1与y2的大小关系是 y1＜y2 ．【考点】反比例函数图象上点的坐标特征． 【分析】反比例函数的系数为﹣5＜0，在每一个象限内，y随x的增大而增大． 【解答】解：∵﹣5＜0， ∴图象位于二、四象限，在每一个象限内，y随x的增大而增大， 又∵x1＜x2＜0， ∴y1＜y2． 故答案为：y1＜y2． 9．（2017锦州数学）如图所示，设A为反比例函数  图象上一点，且矩形ABOC的面积为3，则k= ﹣3 ． 【考点】反比例函数系数k的几何意义． 【分析】因为过双曲线上任意一点引x轴、y轴垂线，所得矩形面积S是个定值，即S=|k|，再根据反比例函数的图象所在的象限即可确定k的值． 【解答】解：由题意得：S=|k|=3，则k=±3； 又由于反比例函数图象位于二、四象限，k＜0， 则k=﹣3． 故答案为：﹣3． 10．如图，在菱形ABCD中，AC与BD相交于点O，AC=8，BD=6，则菱形的边长AB= 5 ．  【考点】菱形的性质． 【分析】（2017锦州数学）根据菱形的对角线互相垂直平分求出OA、OB，再利用勾股定理列式进行计算即可得解． 【解答】解：∵四边形ABCD是菱形， ∴OA=  AC，OB=BD，AC⊥BD，∵AC=8，BD=6， ∴OA=4，OB=3， ∴AB=  =5，故答案为：5． 11．（2017锦州数学）如图，过矩形ABCD对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．若AB= ，∠DCF=30°，则EF长为 2 ．【考点】矩形的性质． 【分析】求出∠ACB=∠DAC，然后利用“角角边”证明△AOF和△COE全等，根据全等三角形对应边相等可得OE=OF，再根据对角线互相垂直平分的四边形是菱形得到四边形AECF是菱形，再求出∠ECF=60°，然后判断出△CEF是等边三角形，根据等边三角形的三条边都相等可得EF=CF，根据矩形的对边相等可得CD=AB，然后求出CF，从而得解． 【解答】解：∵四边形ABCD是矩形 ∴AD∥BC， ∴∠ACB=∠DAC， ∵O是AC的中点， ∴AO=CO， 在△AOF和△COE中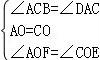，  ，∴△AOF≌△COE（ASA）， ∴OE=OF， 又∵EF⊥AC， ∴四边形AECF是菱形， ∵∠DCF=30°， ∴∠ECF=90°﹣30°=60°， ∴△CEF是等边三角形， ∴EF=CF， ∵AB=  ，∴CD=AB= ，∵∠DCF=30°， ∴CF= ÷ =2，∴EF=2． 故答案为：2． 12．（2017锦州数学）如图，矩形ABCD的面积为20cm2，对角线交于点O；以AB、AO为邻边作平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边作平行四边形AO1C2B；…；依此类推，则平行四边形AO4C5B的面积为 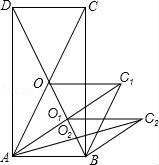 ． 【考点】矩形的性质；平行四边形的性质． 【分析】（2017锦州数学）根据矩形的性质求出△AOB的面积等于矩形ABCD的面积的  ，求出△AOB的面积，再分别求出△ABO1、△ABO2、△ABO3、△ABO4的面积，即可得出答案．【解答】解：∵四边形ABCD是矩形， ∴AO=CO，BO=DO，DC∥AB，DC=AB， ∴S△ADC=S△ABC= S矩形ABCD=×20=10，∴S△AOB=S△BCO= S△ABC=×10=5，∴S  =S△AOB=×5= ，∴S  =S= ，S  =S= ，S  =S= ，∴S  =2S=2× = 故答案为： ．三、（2017锦州数学）计算题：（每小题24分，共24分） 13．解方程 （1）（x﹣3）2=25（直开法） （2）x2+3x+2=0（十字相乘法） （3）x2﹣6x+8=0（配方法） （4）x2﹣x﹣1=0（公式法） 【考点】解一元二次方程﹣因式分解法；解一元二次方程﹣直接开平方法；解一元二次方程﹣配方法；解一元二次方程﹣公式法． 【分析】（1）直接利用开平方法解方程得出答案； （2）直接利用十字相乘法分解因式得出答案； （3）直接利用配方法解方程得出答案； （4）直接利用公式法解方程得出答案． 【解答】解：（1）（x﹣3）2=25（直开法） x﹣3=±5， 解得：x1=8，x2=﹣2； （2）x2+3x+2=0（十字相乘法） （x+1）（x+2）=0， 解得：x1=﹣1，x2=﹣2； （3）x2﹣6x+8=0（配方法） （x﹣3）2=1， 则x﹣3=±1， 解得：x1=2，x2=4； （4）x2﹣x﹣1=0（公式法） b2﹣4ac=1+4=5， 则x=  ，解得：x1=  ，x2= ．四、（2017锦州数学）解答题（17小题12分，18小题14分，19小题14分，共40分） 14．如图，在宽为20m，长为32m的矩形地上，修筑同样宽的三条道路，把耕地分成大小不等的六块，要使耕地面积为570m2，求道路的宽为多少米？ 【考点】一元二次方程的应用． 【分析】把修筑的三条道路分别平移到矩形的最左边和最上边，则剩余的耕地也是一个矩形，设道路的宽为x米，根据矩形面积公式列方程，然后求出解． 【解答】解：设道路的宽为x米， 依题意得（32﹣2x）（20﹣x）=570， 解得x1=1 x2=35（不符合题意舍去）． 答：道路的宽为1米． 15．（2017锦州数学）某水果批发商场经营一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要尽量减少库存，那么每千克应涨价多少元？ 【考点】一元二次方程的应用． 【分析】设每千克应涨价x元，根据每千克涨价1元，销售量将减少20千克，每天盈利6000元，列出方程，求解即可． 【解答】解：设每千克应涨价x元，由题意列方程得： （10+x）=6000， 解得：x=5或x=10， 要尽量减少库存，那么每千克应涨价5元； 答：每千克应涨价5元． 16．（2017锦州数学）如图，已知E是平行四边形ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F． （1）求证：△ABE≌△FCE； （2）连接AC、BF，若BC=2AE，求证：四边形ABFC为矩形； （3）在（2）条件下，当△ABC再满足一个什么条件时，四边形ABFC为正方形．（不需证明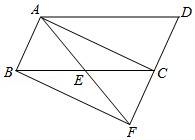）  【考点】四边形综合题． 【分析】（1）根据平行线的性质，可以利用AAS或ASA判断． （2）根据对角线相等的平行四边形是矩形证明即可． （3）结论：当△ABC为等腰三角形时，即AB=AC时，四边形ABFC为正方形；根据邻边相等的矩形是正方形即可证明． 【解答】证明：（1）∵四边形ABCD为平行四边形， ∴AB∥DC， ∴∠ABE=∠ECF， ∵E为BC的中点， ∴BE=CE， 在△ABE和△FCE中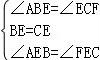，  ，∴△ABE≌△FCE（ASA）； （2）∵△ABE≌△FCE， ∴BE=EC，AE=EF， ∴四边形ABFC为平行四边形， ∵AE= BC，∴AF=BC， ∴四边形ABFC为矩形（对角线相等的平行四边形是矩形）； （3）当△ABC为等腰三角形时，即AB=AC时，四边形ABFC为正方形； 理由如下： 由（2）可知四边形ABFC是矩形， ∵AB=AC， ∴四边形ABFC为正方形（邻边相等的矩形是正方形）． 故答案为：AB=AC．  第1页（共15页） (责任编辑：admin) |