|
☆☆☆ 点击下载试题 ☆☆☆ 机密★启用前 各位同学在查看时请点击全屏查看 2018年遵义中考数学模拟试题 (全卷总分150分,考试时间120分钟) 注意事项: 1．答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。 2．答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦擦干净后，再选涂其它答案标号。 3．答非选择题时，必须使用0.5毫米黑色签字笔将答案书写在答题卡规定的位置上。 4．所有题目必须在答题卡上作答，在试题卷上答题无效。 5．考试结束后,将试题卷和答题卡一并交回。 一、选择题（本题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符号题目要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满。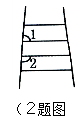）  1．-3的相反数是A．-3 B．  C． D．32．如图，梯子的各条横档互相平行，若∠1＝  ，则∠2的度数是 Ａ． Ｂ．  Ｃ． Ｄ． 3．下列图形中既是中心对称图形,又是轴对称图形的是 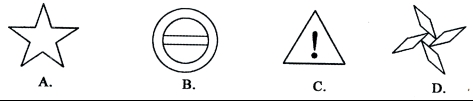 4．计算  的结果是Ａ．  Ｂ． Ｃ． Ｄ． 5．不等式  ≤0的解集在数轴上表示为  6．如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂 上阴影,能构成这个正方体的表面展开图的概率是 Ａ．  Ｂ． Ｃ． Ｄ．  7．函数 的自变量 的取值范围是Ａ．  ＞-2 Ｂ．＜2 Ｃ．≠2 Ｄ．≠-28．一组数据2、1、5、4的方差是 Ａ．10 Ｂ．3 Ｃ．2.5 Ｄ．0.75 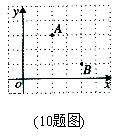 9．如图，两条抛物线 、 与分别经过点 , 且平行于 轴的两条平行线围成的阴影部分的面积为Ａ．8 Ｂ．6 Ｃ．10 Ｄ．4 10．在一次 “寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志 点A  、B ,A、B两点到“宝藏”点的距离都是 ，则“宝藏”点的坐标是 A．  Ｂ． Ｃ． 或 Ｄ． 或 二、填空题(本题共8小题，每小题4分，共32分。答题请用0.5毫米黑色墨水的签字笔或钢笔直接答在答题卡的相应位置上。) 11．太阳半径约为696000千米,数字696000用科学记数法表示为 ▲ . 12．分解因式:  = ▲ . 13．如图,△ABC内接于⊙O,∠C=  ,则∠ABO= ▲ 度.14．如图,已知正方形的边长为  ,以对角的两个顶点为圆心,  长为半径画弧,则所得到的两条弧的长度之和为 ▲  (结果保留 ).15．如图,在宽为  ,长为 的矩形地面上修建两条宽都是 的道路,余下部分种植花草.那么,种植花草的面积为 ▲  .16．已知  ，则 ▲ .  17．小明玩一种的游戏,每次挪动珠子的颗数与对应所得的分数如下表:
当对应所得分数为132分时,则挪动的珠子数为 ▲ 颗. 18．如图，在第一象限内,点P,M  是双曲线 上的两点,PA⊥ 轴于点A,MB⊥轴于点B,PA与OM交于点C,则△OAC的面积为 ▲ .三、解答题(本题共9小题，共88分。答题请用0.5毫米黑色墨水签字笔或钢笔书写在答题卡的相应位置上。解答是应写出必要的文字说明，证明过程或演算步骤。) 19．(6分)计算:  20．(8分)解方程：  21．(8分)在一个不透明的盒子里，装有三个分别写有数字-1、0、1的乒乓球(形状、大小一样)，先从盒子里随机取出一个乒乓球，记下数字后放回盒子，摇匀后再随机取 出一个乒乓球，记下数字. (1)请用树状图或列表的方法求两次取出乒乓球上的数字相同的概率； (2)求两次取出乒乓球上的数字之积等于0的概率. 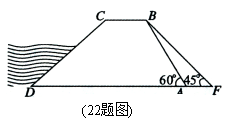 22．(10分)如图,水坝的横断面是梯形,背水坡AB的坡 角∠BAD=  ,坡长AB= ,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡 的坡角∠F=  ,求AF的长度(结果精确到1米,参考数据:  , ).23．(10分)某校七年级(1)班为了在王强和李军两同学中选班长,进行了一次“演讲”与“民主测评”活动，A、B、C、D、E五位老师作为评委对王强、李军的“演讲”打分；该班50名同学分别对王强和李军按“好”、“较好”、“一般”三个等级进行民主测评。统计结果如下图、表.计分规则: ①“演讲”得分按“去掉一个最高分和一个最低分后计算平均分”； ②“民主测评”分＝“好”票数×2分+“较好”票数×1分+“一般”票数×0分； ③综合分＝“演讲”得分×40%＋“民主测评”得分×60%. 解答下列问题: (1)演讲得分,王强得 ▲ 分;李军得 ▲ 分; (2)民主测评得分,王强得 ▲ 分; 李军得 ▲ 分; (3)以综合得分高的当选班长,王强和李军谁能当班长?为什么? 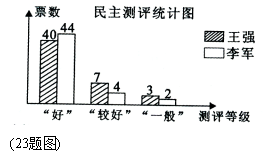  演讲得分表（单位：分）
24．（10分）如图（1），在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝  ，AB与CE交于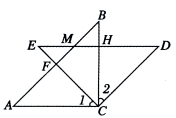F，ED与AB、BC分别交于M、H．(1)求证:CF＝CH；   (2)如图(2)，△ABC不动，将△EDC绕点C旋转到∠BCE= 时，试判断四边形ACDM是什么四边形？并证明你的结论．  25．（10分）某酒厂每天生产A、B两种品牌的白酒共600瓶，A、B两种品牌的白酒每瓶的成本和利润如下表：
设每天生产A种品牌的白酒  瓶，每天获利 元．(1)请写出  关于的函数关系式；(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元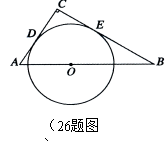？  26．（12分）如图，在△ABC中，∠C= ，AC+BC=8，点O是斜边AB上一点，以O为圆心的⊙O分别与AC、BC相切于 点D、E． （1）当AC＝2时，求⊙O的半径； （2）设AC＝ ，⊙O的半径为，求与的函数关系式．27．（14分）如图，已知抛物线 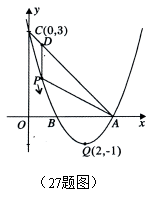 的顶点坐 标为Q ，且与轴交于点C ，与轴交于A、B两点（点A在点B的右侧），点P是该抛物线上一动点，从点C 沿抛物线向点A运动（点P与A不重合），过点P作PD∥ 轴，交AC于点D． (1)求该抛物线的函数关系式； (2)当△ADP是直角三角形时，求点P的坐标； (3)在问题(2)的结论下，若点E在 轴上，点F在抛物线上，问是否存在以A、P、E、F为顶点的平行四边形？若存在， 求点F的坐标；若不存在，请说明理由． 机密★启用前 2018年遵义中考数学模拟试题参考答案 一、选择题（每小题3分，共30分）
二、填空题(每小题4分，共32分) 11．6.96×  12． 13．50 14． 15．1131 16．2010 17．12 18．  三、解答题(共9小题，共88分) 19．(6分)解: = =  20．(8分)解：方程两边同乘以  ,得: 合并:2  -5＝-3∴  ＝1经检验， ＝1是原方程的解． 21．(8分)解：(1)树状图为:共9种情况,两次数字相同的有3种. ∴P(两次数字相同)＝  （2）（2分）数字之积为0有5种情况， ∴Ｐ(两数之积为0)  22．(10分)解：过Ｂ作BE⊥AD于E 在Rt△ABE中,∠BAE= 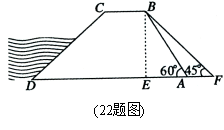 , ∴∠ABE=  ∴AE＝ ＡＢ ∴BE  ∴在Rt△BEF中, ∠Ｆ＝  , ∴EF＝BE＝30∴ＡＦ＝ＥＦ－ＡＥ＝30－  ∵  ， ∴AF＝12.68 1323．(10分)解: (1)(4分)王强得 92 分;李军得 89 分; (2)(4分)民主测评王强得 87 分; 李军得 92 分; (3)(2分)王强综合分=92×40%＋87×60%=89分 李军综合分=89×40%＋92×60%=90.8分 ∵90.8＞89, ∴李军当班长. 24．（10分）解:(1)(5分) 证明:在△ACB和△ECD中 ∵∠ACB=∠ECD= ∴∠1+∠ECB=∠2+∠ECB, ∴∠1=∠2 又∵AC=CE=CB=CD, ∴∠A=∠D=  ∴△ACB≌△ECD, ∴CF=CH (2)(5分) 答: 四边形ACDM是菱形 证明: ∵∠ACB=∠ECD=, ∠BCE=∴∠1= , ∠2=又∵∠E=∠B= ,∴∠1=∠E, ∠2=∠B ∴AC∥MD, CD∥AM , ∴ACDM是平行四边形 又∵AC=CD, ∴ACDM是菱形 25．（10分）解:(1)(4分) =20+15(600-)即 =5+9000(2)(6分)根据题意得: 50 +35(600-)≥26400∴  ≥360当 =360时, 有最小值,代入=5+9000得=5×360+9000=10800∴每天至少获利10800元. 26．（12分）(1)(5分) 解: 连接OD、OE、OC ∵D、E为切点 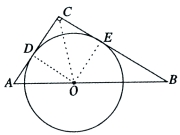 ∴OD⊥AC， OE⊥BC， OD=OE∵  ∴  AC·BC=AC·OD+BC·OE∵AC+BC=8， AC=2，∴BC=6 ∴ ×2×6=×2×OD+×6×OE而OD=OE， ∴OD=  ，即⊙O的半径为 （2）（7分）解：连接OD、OE、OC ∵D、E为切点 ∴OD⊥AC， OE⊥BC， OD=OE= ∵ ∴ AC·BC=AC·OD+BC·OE∵AC+BC=8， AC=  ，∴BC=8-∴ （8-）= +（8-）化简：  即：  27．（14分）解：（1）（3分） ∵抛物线的顶点为Q（2，-1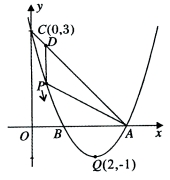）  ∴设 将C（0，3）代入上式，得   ∴  ， 即 （2）（7分）分两种情况： ①(3分)当点P1为直角顶点时,点P1与点B重合(如图) 令  =0, 得 解之得  ,  ∵点A在点B的右边, ∴B(1,0), A(3,0) ∴P1(1,0) ②(4分)解:当点A为△APD2的直角顶点是(如图) ∵OA=OC, ∠AOC=  , ∴∠OAD2= 当∠D2AP2= 时, ∠OAP2=, ∴AO平分∠D2AP2又∵P2D2∥ 轴, ∴P2D2⊥AO, ∴P2、D2关于轴对称.设直线AC的函数关系式为  将A(3,0), C(0,3)代入上式得 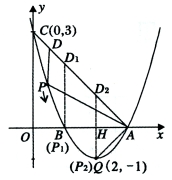  , ∴ ∴  ∵D2在  上, P2在上,∴设D2( , ), P2(, )∴( )+( )=0 , ∴ , (舍)∴当 =2时, =  =-1∴P2的坐标为P2(2,-1)(即为抛物线顶点) ∴P点坐标为P1(1,0), P2(2,-1) (3)(4分)解: 由题(2)知,当点P的坐标为P1(1,0)时,不能构成平行四边形 当点P的坐标为P2(2,-1)(即顶点Q)时, 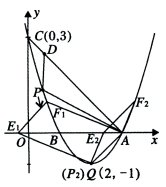 平移直线AP(如图)交轴于点E,交抛物线于点F.当AP=FE时,四边形PAFE是平行四边形 ∵P(2,-1), ∴可令F( ,1)∴  解之得:  ,  ∴F点有两点,即F1(  ,1), F2( ,1)1 (责任编辑：admin) |