 
此试题可能存在乱码情况,在查看时请点击右上角全屏查看
2017年湘潭中考数学试题
考试时量:120分钟 满分:120分
一、选择题:本大题共8个小题,每小题有且只有一个正确答案,请将正确答案的选项代号涂在答题卡相应的位置上,每小题3分,满分24分)
1.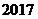 的倒数是( ) 的倒数是( )
A.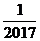 B. B.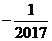 C. C.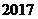 D. D.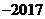
【答案】A
【解析】
试题分析:性质符号相同,分子分母位置颠倒的两个数称为互为倒数,所以2117的倒数是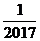
考点:互为倒数的定义
2.如图所示的几何体的主视图是( )
A. 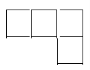 B. B.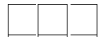 C. C. 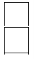 D. D. 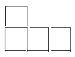 
【答案】D
【解析】试题分析:三视图就是主视图(正视图)、俯视图、左视图的总称。从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状;从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状;从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状。
 从正面看到的图是 从正面看到的图是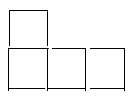 ,故选D ,故选D
考点:三视图
3.不等式组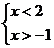 的解 的解 集在数轴上表示为( ) 集在数轴上表示为( )
A. B. B.
C. D. D.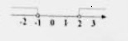
【答案】B
【解析】试题分析:x<2,不包括2,画空心圆圈,小于向左拐;x>-1,不包括-12,画空心圆圈,大于向右拐,故选B
考点:不等式
4.下列计算正确的是( )
A.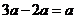 B. B.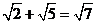 C. C.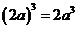 D. D.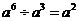
【答案】A
【解析】试题分析:A.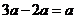 正确 B. 正确 B.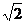 和 和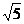 无法进行加法运算 C. 无法进行加法运算 C. 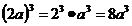 D. D.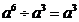 ,故选A ,故选A
考点:代数式的运算
5.“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
| 阅读数量 | 1本 | 2本 | 3本 | 3本以上 | | 人数(人) | 10 | 18 | 13 | 4 |
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数 B.中位数 C.众数 D.方差
【答案】C
【解析】
试题分析:用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中 位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…xn的平均数为 位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…xn的平均数为 ,则方差S2= ,则方差S2= [(x1﹣ [(x1﹣ )2+(x2﹣ )2+(x2﹣ )2+…+(xn﹣ )2+…+(xn﹣ )2]. )2].
45个 数据中,数据2共18个,个数最多,故选C
考点:方差;平均数;中位数;众数
6.函数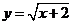 中,自变量 中,自变量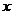 的取值范围是( ) 的取值范围是( )
A.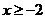 B. B.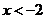 C. C. 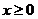 D. D.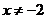
【答案】A
【解析】
试题分析: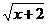 中,x+2≥2,∴ 中,x+2≥2,∴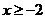 故选C 故选C
考点:二次根式
7.如图,在半径为4的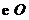 中, 中,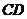 是直径, 是直径,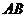 是弦,且 是弦,且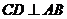 ,垂足为点 ,垂足为点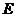 , ,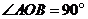 ,则阴影部分的面积是( ) ,则阴影部分的面积是( )

A.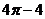  B. B.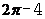 C. C.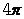 D. D.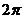
【答案】D
【解析】
试题分析:∵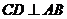 ,∴ ,∴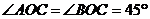 ,∴ ,∴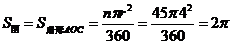 ,故选C ,故选C
考点:垂径定理,扇形的面积
8.一次函数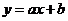 的图象如图所示,则不等式 的图象如图所示,则不等式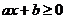 的解集是( ) 的解集是( )
 
A.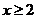 B. B.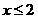 C. C.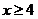 D. D.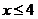
【答案】A
【解析】
试题分析: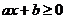 ,即y≥0,观察图形知, ,即y≥0,观察图形知,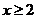 故选C 故选C
考点:一次函数与不等式的关系
二、填空题(本题共8个小题,请将答案写在答题卡相应的位置上,每小题3分,满分24分)
9.因式分解: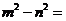 . .
【答案】 (m+n)(m- (m+n)(m- n) n)
【解析】
试题分析:利用平方差公式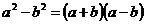 ,知 ,知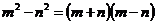
考点:因式分解
- 截止2016年底,到韶山观看大型实景剧《中国出了个毛泽东》的观众约为925000人次,将925000用科学计数法表示为 .
【答案】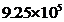
【解析】
试题分析:科学记数法的表示形式为a×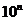 的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数. 的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
所以,925000用科学计数法可表示为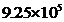
考点:科学记数法的表示方法
- 计算:
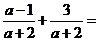 . .
【答案】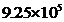
【解析】
试题分析: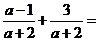 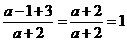
考点:分式的运算
12.某同学家长应邀安参加孩子就读中学的开放日活动,他打算上午随机听一节孩子所在1班的课,下表是他拿到的当天上午1班的课表,如果每一节课被听的机会均等,那么他听数学课的概率是 .
 [来源:] [来源:]
【答案】
【解析】
试题分析:随机听一节孩子所在1班的课,一共4中情况,听数学只占1只占一种情况,∴概率是
考点:简单的概率计算
13.如图,在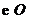 中,已知 中,已知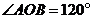 ,则 ,则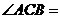 . .
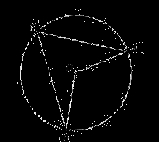
【答案】60°
【解析】
试题分析:利用知识点:一条弧所对圆周角等于它所对圆心角的一半,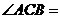 60° 60°
考点:圆周角定理
14.如图,在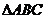 中, 中,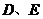 分别是边 分别是边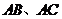 的中点,则 的中点,则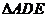 与 与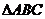 的面积比 的面积比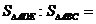 . .

【答案】
【解析】
试题分析:∵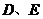 分别是边 分别是边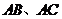 的中点,∴DE是三角形的中位线,∴ 的中点,∴DE是三角形的中位线,∴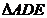 ∽ ∽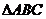
∴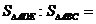 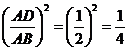
考点:相似三角形及中位线性质定理
15.如图,在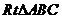 中 中 , ,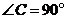 , ,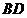 平分 平分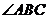 交 交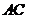 于点 于点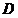 , ,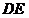 垂直平分 垂直平分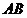 ,垂足为 ,垂足为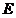 点,请任意写出一组相等的线段 点,请任意写出一组相等的线段  . .
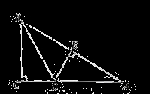
【答案】BC=BE或DC=DE
【解析】
试题分析:利用角平分线性质定理,知BC=BE;利用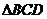 ∽ ∽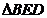 ,得DC=DE ,得DC=DE
考点:角平分线性质定理
- 阅读材料:设
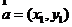 , , ,如果 ,如果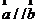 ,则 ,则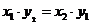 .根据该材料填空:已知 .根据该材料填空:已知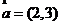 , ,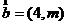 ,且 ,且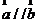 ,则 ,则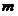 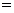 . .
【答案】6
【解析】
试题分析:利用新定义设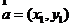 , , ,如果 ,如果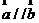 ,则 ,则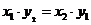 ,2m=4×3,m=6 ,2m=4×3,m=6
考点:新定义问题
三、解答题 (本大题共10小题,解答应写出文字说明、证明过程或演算步骤.请将解答过程写在答题卡相应位置上,满分72分) [来源:]
17.计算: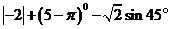
考点:(1)、实数运算;(2)、三角函数
【解析】试题分析:首先根据0 次幂、绝对值以及三角函数的计算法则求出各式的值,然后进行求和. 次幂、绝对值以及三角函数的计算法则求出各式的值,然后进行求和.
【解答】
原式=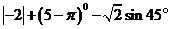 = =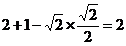
18. “鸡兔同笼”是我国古代著名的数学趣题之一.大约在1500年前成书的《孙子算经》中,就有关于“鸡兔同笼”的记载:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有35个头;从下面数,有94条腿.问笼中各有几只鸡和兔?
考点:二元一次方程组的应用
【解析】试题分析:设笼中各有x只鸡,y只兔,根据:①鸡数+兔数=35,②鸡足+兔足=94,列出方程组求解可得.
【解答】
解:设笼中各有x只鸡,y只兔,根据题意得
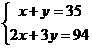
解得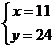
∴笼中各有11只鸡,24只兔
19. 从这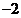 ,1, ,1,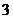 三个数中任取两个不同的数,作为点的坐标. 三个数中任取两个不同的数,作为点的坐标.
(1)写出该点所有可能的坐标;
(2)求该点在第一象限的概率.
考点:树状图或列表求概率
【解析】试题分析:列表如图:
| -2 | 1 | 3 | | -2 | (-2,-2) | (-2,1) | (-2,3) | | 1 | (1,-2) | (1,1) | (1,3) | | 3 | (3,-2) | (3,1) | (3,3) |
由表可知该点在第一象限的概率为 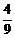
【解答】
(1)见解析;(2)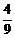
20. 如图,在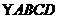 中, 中,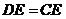 连接 连接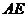 并延长交 并延长交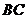 的延长线于点 的延长线于点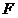 . .
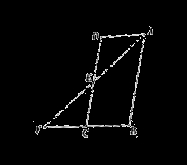
(1)求证: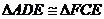 ; ;
(2)若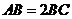 , ,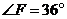 ,求 ,求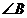 的度数. 的度数.
考点:平行四边形,全等三角形
【解析】试题分析:(1)利用AAS或ASA,证明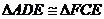 .(2)先证明三角形ABF是等腰三角形,再 .(2)先证明三角形ABF是等腰三角形,再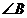 的度数. 的度数.
【解答】
(1)∵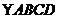
∴AD∥DF
∴∠ADE=∠EFC
∵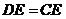 ,∠AED=∠CEF ,∠AED=∠CEF
∴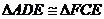
(2)∵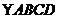
∴AD=BC
∵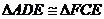
∴AD=FC[来源:学,科,网]
∴FC=BC
∵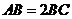
∴AB=BF
∵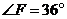
∴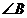 =108° =108°
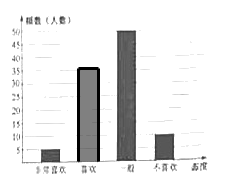
21.为响应习总书记足球进校园的号召,某学校积极开展与足球有关的宣传与实践活动.学生会体育部为了解本学校对足球运动的态度,随机抽取了部分学生进行调查,并绘制了如下的统计图表(部分信息未给出).
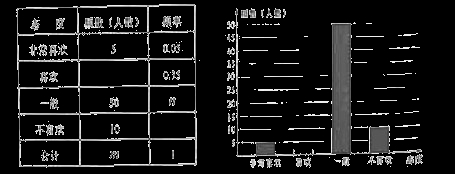
(1)在上面的统计表中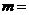 , ,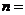 . .
(2)请你将条形统计图补充完整;
(3)该校共有学生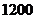 人,根据统计信息,估计爱好足球运动(包括喜欢和非常喜欢)的学生有多少人? 人,根据统计信息,估计爱好足球运动(包括喜欢和非常喜欢)的学生有多少人?
【解析】
(1)利用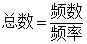 ,求得总数100人,再求m=40 ,求得总数100人,再求m=40
(2)先求出喜欢足球人数35人,再将条形统计图补充完整
(3)1200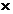 (0.05+0.35)=480 (0.05+0.35)=480
【解】
(1)m=5÷0.05-50-10=40,n=50÷100=0.5
(2)100 0.35=35 0.35=35
图形如下:
(3)1200 (0.05+0.35)=480 (0.05+0.35)=480
 考点:统计图 考点:统计图
22.由多项式乘法: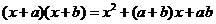 ,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式: ,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式:
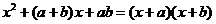
示例: 分解因式: 分解因式: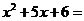 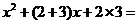 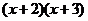
(1)尝试:分解因式: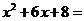 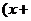 ___ ___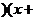 ___); ___);
(2)应用:请用上述方法解方程: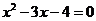 . .
【解析】
(1)把8分解成2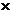 4,且2+4=6 4,且2+4=6
(2)把-4分解成1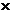 (-4),且1+(-4)=-3 (-4),且1+(-4)=-3
【解】
(1)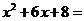 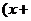 _2_ _2_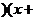 _4_); _4_);
(2)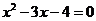
解:
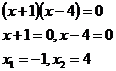
 考点:“十字相乘法”因式分解,解一元二次方程 考点:“十字相乘法”因式分解,解一元二次方程
23.某游乐场部分平面图如图所示, 在同一直线上, 在同一直线上,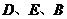 在同一直线上,测得 在同一直线上,测得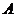 处与 处与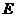 处的距离为 处的距离为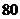 米, 米,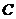 处与 处与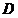 处的距离为 处的距离为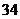 米, 米,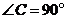 , ,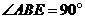 , ,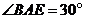 . .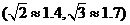 

(1)求旋转木马 处到出口 处到出口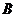 处的距离; 处的距离;
(2)求海洋球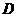 处到出口 处到出口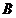 处的距离(结果保留整数). 处的距离(结果保留整数).
【解析】
(1)利用BE=AEsin30°,求BE
(2)利用DE=CDCOS30°,求DE
【解】
(1)∵AE=80,∠BAE=30°,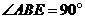
∴BE= AEsin3 AEsin3 0°=80× 0°=80× =40米 =40米
(2)∵∠CED=∠AEB,∠DCE=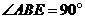
∴∠D=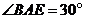
∵CD=34米
∴DE=CDCOS30°=34×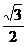 = =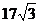
∴DB=DE+BE=40+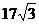
 考点:三角函数的应用 考点:三角函数的应用
24.已知反比例函数 的图象过点 的图象过点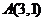 . .
(1)求反比例函数的解析式;
(2)若一次函数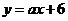 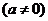 的图象与 的图象与 反比例函数的图象只有一个交点,求一次函数的解析式. 反比例函数的图象只有一个交点,求一次函数的解析式.
【解析】
(1)把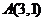 代入 代入 得 得
(2)由一次函数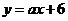 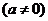 的图象与反比例函数的图象只有一个交点,知 的图象与反比例函数的图象只有一个交点,知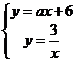 只有一组解, 只有一组解,
得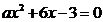 有2个相等的实数根,再利用 有2个相等的实数根,再利用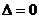 求a 求a
【解】
(1)∵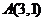
∴
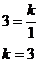
∴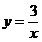
(2)∵一次函数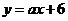 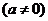 的图象与反比例函数 的图象与反比例函数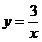 的图象只有一个交点 的图象只有一个交点
∴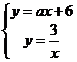 只有一组解 只有一组解
∴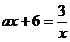 只有一组解 只有一组解
∴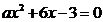 有2个相等的实数根 有2个相等的实数根
∴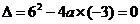
a= -3
∴y= -3x+6
 考点:一次函数与反比例函数 考点:一次函数与反比例函数
25.已知抛物线的解析式 为 为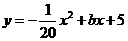 . .
(1)当自变量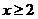 时,函数值 时,函数值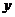 随 随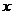 的增大而减少,求 的增大而减少,求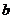 的取值范围; 的取值范围;
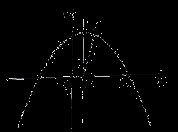
(2)如图,若抛物线的图象经过点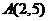 ,与 ,与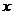 轴交于点 轴交于点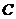 ,抛物线的对称轴与 ,抛物线的对称轴与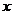 轴交于 轴交于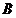 . .
①求抛物线的解析式;
②在抛物线上是否存在点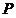 ,使得 ,使得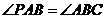 ?若存在,求出点 ?若存在,求出点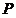 的坐标;若不存在,请说明理由. 的坐标;若不存在,请说明理由.
【解析】
(1)∵自变量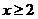 时,函数值 时,函数值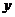 随 随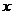 的增大而减少,∴ 的增大而减少,∴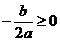 ,b≥0 ,b≥0
(2)①把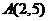 代入 代入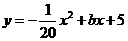 ,得 ,得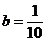
②作线段AB的垂直平分线,交抛物线于两点,此时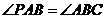
【解】
(1)∵自变量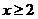 时,函数值 时,函数值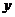 随 随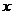 的增大而减少 的增大而减少
∴对称轴在直线x=2的右边
∴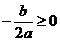
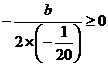
b≥0
(2)①把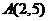 代入 代入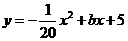 ,得 ,得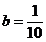
∴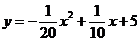
②存在
作线 段AB的垂直平分线,与抛物线交于两点,此时 段AB的垂直平分线,与抛物线交于两点,此时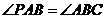
抛物线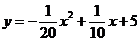 的对称轴是直线x=1,则B(1,0) 的对称轴是直线x=1,则B(1,0)
∵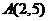
∴直线AB表达式y=5x-5,E(1.5,2.5)
∴直线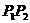 表达式k= 表达式k=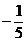
设直线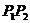 表达式 表达式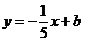
把E(1.5,2.5)代入表达式得,b=2.8
直线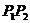 表达式 表达式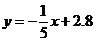
由题意得
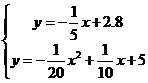
解得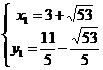 , ,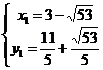
∴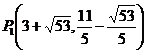 , ,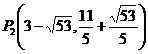
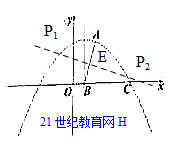
 考点:二次函数 考点:二次函数
26.如图,动点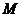 在以 在以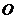 为圆心, 为圆心,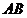 为直径的半圆弧上运动(点 为直径的半圆弧上运动(点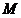 不与点 不与点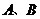 及 及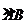 的中点 的中点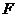 重合),连接 重合),连接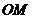 .过点 .过点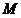 作 作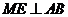 于点 于点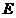 ,以 ,以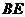 为边在半圆同侧作正方形 为边在半圆同侧作正方形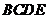 ,过 ,过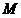 点作 点作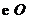 的切线交射线 的切线交射线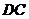 于点 于点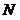 ,连接 ,连接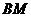  、 、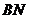 . .
(1)探究:如左图,当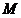 动点在 动点在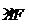 上运动时; 上运动时;
①判断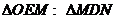 是否成立?请说明理由; 是否成立?请说明理由;
②设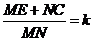 , ,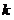 是否为定值?若是,求出该定值,若不是,请说明理由; 是否为定值?若是,求出该定值,若不是,请说明理由;
③设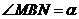 , ,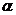 是否为定值?若是,求出该定值,若不是,请说明理由; 是否为定值?若是,求出该定值,若不是,请说明理由;
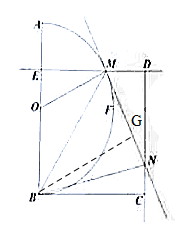
(2)拓展:如右图,当动点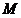 在 在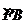 上运动时; 上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
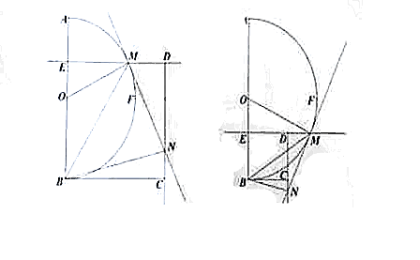
  [来源:.Com] [来源:.Com]
 
(责任编辑:admin) |