|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看 2018年株洲中考数学复习题 一、选择题 本大题共有 10 小题，每小题 3 分，共 30 分.在每小题所给出的四个选项中，恰 有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上. 1. 5 的绝对值是 （ ） 1 1A. 5 B. C. 5 D. 5 52. 若式子 2x 1 在实数范围内有意义，则 x 的取值范围是 （ ） A. x 1 2B. x 1 2C. x 1 2D. x 1 23. 下列计算正确的是 ( ) A. a4 a3 1 B. a4 a3 a7 C. (2a3 )4 8a12 D. a4 a3 a7 4. 下列各图中，不是中心对称图形的是 ( )   CO A B （第 8 题） （第 9 题） 5. 在一个不透明的盒子里有 3 个红球和 n 个白球，这些球除颜色外其余完全相同，摇匀后 1随机摸出一个，摸到红球的概率是 ，则 n 的值为 ( ) 3A. 9 B. 4 C. 6 D. 8 6. 一个圆锥的底面半径为 3，母线长为 5，则圆锥的侧面积是 （ ） A.9π B.18π C.15π D.27π 7．已知二次函数 y=x2﹣3x+m（m 为常数）的图象与 x 轴的一个交点为（1，0），则关于 x 的 一元二次方程 x2﹣3x+m=0 的两实数根是 （ ） A． x1=1，x2=﹣1 B． x1=1，x2=2 C． x1=1，x2=0 D． x1=1，x2=3 8．如图，△ABC 内接于⊙O，连接 OA，OB，∠C =40°，则∠OBA 的度数是( ) A．60° B．50° C．45° D．40° 9．如图，在△ABC 中，AB＝6，AC＝8，BC＝10，D、E 分别是 AC、AB 的中点，则以 DE 为直 径的圆与 BC 的位置关系是 ( ) A．相切 B．相交 C．相离 D．无法确定 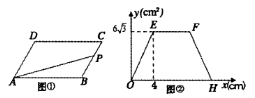 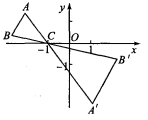 （第 10 题） （第 16 题）  10. 如图①，在 ▱ ABCD 中， B 120，动点 P 从点 B 出发，沿 BC 、 CD 、 DA 运动 至点 A 停止.设点 P 运动的路程为 x cm, PAB 的面积为 y cm2， y 关于 x 的函数的图 像如图(2)所示，则图②中 H 点的横坐标为 ( ) A. 11 B. 14 C. 8 D. 8 3 3 二、填空题 (本大题共 8 小题，每小题 3 分，共 24 分) 11.人的眼睛可以看见的红光的波长是 0.000077 cm，请把这个数用科学记数法表示，其结 果是 cm. 12 .函数 y 中自变量 x 的取值范围是 ． 13 .分解因式：a3－2a2b＋ab2＝ ． 14. 一个正多边形的每一个外角都是 72°，那么这个多边形是 边形. 15.有一组数据如下：3、7、4、6、5，那么这组数据的方差是 ． 16.如图，在△ABC 中，A、B 两个顶点在 x 轴的上方，点 C 的坐标是(－1，0).以点 C 为位似 中心，在 x 轴的下方作△ABC 的位似图形△A'B'C，并把△ABC 的边长放大到原来的 2 倍．设 点 B 的对应点 B'的横坐标是 2，则点 B 的横坐标是 ． 17．已知 M、N 两点关于 y 轴对称，且点 M 在双曲线 y＝ 1 2x 上，点 N 在直线 y＝x＋3 上，设 点 M 的坐标为（a，b），则 y＝－abx2＋(a＋b)x 的顶点坐标为 ． 418. 如图，已知点 A1 , A2 , … , An 均在直线 y x 2 上，点 B1 , B2 , …, Bn 均在双曲线 y x  上，并且满足: A1B1 x 轴， B1 A2 y 轴， A2 B2 x 轴， B2 A3 y 轴，…， An Bn x 轴， Bn An1 y 轴，…，记点 An 的横坐标为 an ( n 为正整数).若 a1 2 ，则 a2016 = . 三、解答题 本大题共 10 小题，共 76 分.把解答过程写在答题纸相对应的位置上，解答时 应写出必要的计算过程、推演步骤或文字说明.作图时用 2B 铅笔或黑色墨水签字笔.19.(5 分）计算： 2 cos 6033 3 2 ． 3x 2 x 2 1  20.（5 分）求不等式组 x 1 7 x 2 2 221．（本小题满分 6 分）先化简 2a 2 a 1 a2 1 ，然后 a 在－1、1、2 三个数中 任选一个合适的数代入求值． a 1 a2 2a 1  22．(本题满分 6 分) 如图,在边长为 1 的小正方形组成的网格中，△ABC 的三个顶点均在格 点上，请按要求完成下列各题： (1)用 2．B．铅．笔．画．．AD∥BC(D 为格点)，连接 CD； (2)线段 CD 的长为 ； (3)请你在△ACD 的三个内角中任选一个锐角，若你所选 的锐角是 ，则它所对应的正弦函数值是 (4)若 E 为 BC 中点，则 tan∠CAE 的值是 ．  23. (8 分）如图，在△ABC 中，AB=CB，∠ABC=90°，D 为 AB 延长线上一点，点 E 在．BC 边上，且 BE=BD，连结 AE、DE、DC．(1)求证：．△ABE≌△CBD； (2)若∠CAE=30°，求∠BDC 的度数．  24. (8 分) 某学校为了提高学生能力，决定开设以下校本课程：A．文学院，B．小小 数学家，C 小小外交家，D．未来科学家．为了解学生最喜欢哪一项校本课程，随机抽取了 部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题： (1)这次被调查的学生共有 人； (2)请你将条形统计图补充完整； (3)在平时的小小外交家的课堂学习中，甲、乙、丙、丁四 人表现优秀，现决定从这四名同学中任选两名参加全国英语 口语大赛，求恰好同时选中甲、乙两位同学的概率（用树状 图或列表法解答）． 25. (8 分) 如图，矩形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上，点 B 的坐标为（2，3）.双曲线 y k ( x 0) 的图象经过 BC 的中点 D，且 1x 与 AB 交于点 E，连接 DE. （1）求 k 的值及点 E 的坐标； （2）若点 F 是 OC 边上一点，△FBC∽△DEB，求直线 FB 的解析式. 26. (10 分) 甲、乙两城市之间开通了动车组高速列车．已知每隔 2 h 有一列速度相同的动 车组列车从甲城开往乙城．如图，OA 是第一列动车组列车离开甲城的路程 s（km）与运行时 间 t（h）的函数图象，BC 是一列从乙城开往甲城的普通快车距甲城的路程 s（km）与运行 时间 t（h）的函数图象．请根据图中的信息，解答下列问题： （1）从图象看，普通快车发车时间比第一列动车组列车发车时间 1 h(填”早” 或”晚”)，点 B 的纵坐标 600 的实际意义是 ； （2）请直接在图中画出第二列动车组列车离开甲城的路程 s（km 与时间 t（h）的函数图象； （3）若普通快车的速度为 100 km/h， ①求第二列动车组列车出发多长时间后与普通快车相遇？ ②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动 车组列车相遇的时间间隔． 1600 400 200 s/km B A M t/h O 1 2 4 6 C (第 23 题) 27. (10 分) 如图，已知抛物线 y 1 x 2 bx c 与坐标轴分别交于点 A（0，8）、B（8， 2 0）和点 E，动点 C 从原点 O 开始沿 OA 方向以每秒 1 个单位长度移动，动点 D 从点 B 开 始沿 BO 方向以每秒 1 个单位长度移动，动点 C、D 同时出发，当动点 D 到达原点 O 时， 点 C、D 停止运动． （1）直接写出抛物线的解析式： （2）求△CED 的面积 S 与 D 点运动时间 t 的函数解析式；当 t 为何值时，△CED 的面积最 大？最大面积是多少？ （3）当△CED 的面积最大时，在抛物线上是否存在点 P（点 E 除外），使△PCD 的面积等 于△CED 的最大面积？若存在，求出 P 点的坐标；若不存在，请说明理由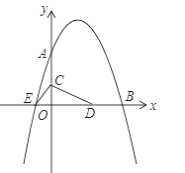．   28.（10 分）如图，Rt△ABC 中，M 为斜边 AB 上一点，且 MB＝MC＝AC＝8cm，平行于 BC 的直 线 l 从 BC 的位置出发以每秒 1cm 的速度向上平移，运动到经过点 M 时停止. 直线 l 分 别交线段 MB、MC、AC 于点 D、E、P，以 DE 为边向下作等边△DEF，设△DEF 与△MBC 重 叠部分的面积为 S（cm2），直线 l 的运动时间为 t（秒）．（1）求边 BC 的长度； （2）求 S 与 t 的函数关系式； （3）在整个运动过程中，是否存在这样的时刻 t，使得以 P、C、F 为顶点的三角形为等腰 三角形？若存在，请求出 t 的值；若不存在，请说明理由． （4）在整个运动过程中，是否存在这样的时刻 t，使得以点 D 为圆心、BD 为半径的圆与直 线 EF 相切？若存在，请求出 t 的值；若不存在，请说明理由． A A M M l D E P B C B C F 备用图 (责任编辑：admin) |