|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况,在查看时请点击右上角全屏查看 2018年株洲中考数学冲刺试题 一、选择题(本大题共12小题,每小题4分,满分48分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1. 要使分式 A. 2. A. 3. 为了响应中央号召,今年永州市加大财政支农力度,全市农业支出累计达到285000 000元,其中285 000 000元用科学记数法可表示为( ) A.2.85×108元 B.0.285×108元 C.2.85×109 元 D.28.5×109元 4. 下列命题中错误的是( ) A.两组对边分别相等的四边形是平行四边形 B.圆内最大的弦是直径 C.有三条边对应相等的两个三角形全等 D.长度相等的弧是等弧 5. 设 A. 6.下面事件:①掷一枚硬币,着地时正面向上;②在标准大气压下,水加热到100℃会沸腾;③买一张福利彩票,开奖后会中奖;④明天会下雨.其中,必然事件有( ) A.1个 B.2个 C.3个 D.4个 7. ⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( ) A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定 8.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是( ) A. 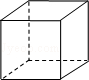 B. B. 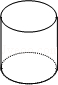 C. C. 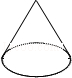 D. D. 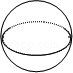 9. 若关于 A.1 B.0,1 C.1,2 D.1,2,3  10.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C =( ) 10.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C =( ) A.30o B.20o C.130o D.90o 11.两个相似三角形的面积比为1:4,那么这两个相似三角形的周长比为( ) A.1:16 B.1:8 C.1:2 D.1:4 12.请观察下列等式的规律: 计算: A. 二、填空题(本大题共8小题,每小题4分,满分32分.) 13.3的倒数等于 . 14.因式分解:4x2y -4xy2 +y3 = . 15.已知△ABC中,BC=6cm,E、F分别是AB、AC的中点,那么EF长是 cm. 16.一个圆锥的母线长为5cm,底面圆半径为3 cm,则这个圆锥的侧面积是 cm2(结果保留  17.如图,已知点C为反比例函数 17.如图,已知点C为反比例函数18.某同学在一次期末测试中,七科的成绩分别是92,100,96,93,96,98,95,则这位同学成绩的中位数和众数分别是 , . 19. 在平面直角坐标系中,点 20.若定义一种新运算x*y=x2-y2,如5*2=52-22=21,那么计算2016*(1008*1007)的结果为 . 三、解答题(本大题共7小题,满分70分,解答应写出文字说明、证明过程或演算步骤) 21.(8分)先化简,再求值:  22.(8分)如图,某人在D处测得山顶C的仰角为30o,向前走200米来到山脚A处,测得山坡AC的坡度为i=1∶0.5,求山的高度.(答案精确到米) 22.(8分)如图,某人在D处测得山顶C的仰角为30o,向前走200米来到山脚A处,测得山坡AC的坡度为i=1∶0.5,求山的高度.(答案精确到米)23.(10分)永州市工业走廊南起祁阳县黎家坪镇,北至冷水滩工业园.在这一走廊内的工业企业2014年完成工业总产值630亿元,如果要在2016年达到907.2亿元. (1)那么2014年到2016年的工业总产值年平均增长率是多少? (2)若2017年按此增长率持续增长,请你预测2017年的工业总产值为多少亿元? 24.(10分)祁阳县某中学校团委开展“关爱残疾学生”爱心捐书活动,全校师生踊跃捐赠各类书籍共3000本.为了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.  (1)这次统计共抽取了 本书籍,扇形统计图中的m= ,∠α的度数是 ; (1)这次统计共抽取了 本书籍,扇形统计图中的m= ,∠α的度数是 ;(2)请将条形统计图补充完整; (3)估计全校师生共捐赠了 多少本文学类书籍. 25.(10分)在菱形ABCD中,P是AB上一动点(但不与A、B两点重合),DP的延长线交CB延长线于点E. (1)△APD与△BPE是否总相似,为什么? (2)当P为AB中点时,求证:点B是EC中点. (3)当PD⊥AB时,设AD=10,sinA=   26.(12分)如图,抛物线 26.(12分)如图,抛物线(1)求 (2)求证:点P在运动过程中,⊙P始终与  (3)设⊙P与 (3)设⊙P与27.(12分)如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE, △AMN是等边三角形. (1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由; (2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是请给出证明,  (3)在(2)的条件下,求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比S△ADE∶S△ABC∶ S△AMN. (3)在(2)的条件下,求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比S△ADE∶S△ABC∶ S△AMN.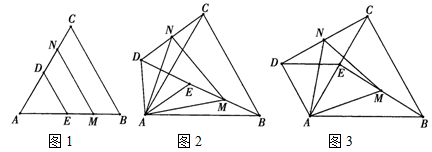 2018年株洲中考数学冲刺试题参考答案 1.B 2.C 3.A 4.D 5.A 6.A 7.B 8.A 9.B 10.B 11.C 12.A 19.(4,-5) 20.4031 21. 原式= 当y=-2时,原式= 22.设山高BC = 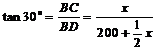 , ,23.(1) 设2014年到2016年的年平均增长率为 x ,则 :630(1+ x)2=907.2. 化简得 :(1+ x)2=1.44,x1=0.2=20%, x2= -2.2(舍去). 答:2014年到2016年的工业总产值年平均增长率为 20%. (2)907.2×1.2=1088.64, 答:预测2017年的工业总产值为1088.64亿元. 24.(1)200,40, 36o (2)B补全到统计图中的高度为60. (3) 30%×3000=900(本). 答:估计全校师生共捐赠了900本文学类书籍. 25.(1)相似. ∵四边形ABCD为菱形,∴AD∥BC.∴∠DAP=∠EBP,∠ADP=∠BEP.∴△APD△BPE. (2)∵P是AB中点,∴AP=BP.又∵∠DAP=∠EBP,∠ADP=∠BEP,∴△APD△BPE. ∴AD=BE. ∵四边形ABCD为菱形, ∴AD=BC.∴BE=BC.即点B为EC中点. (3)∵PD⊥AB,AD=10,sinA= ∵△APD∽△BPE,∴ 26. (1) (2)设P(x,y), ⊙P的半径r= (3)设P( 又A(0,2),∴AM= 当AM=AN时,解得 当AM=MN时, 当AN=MN时, 综上所述,P的纵坐标为0或 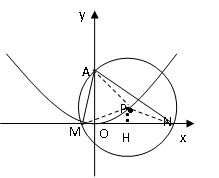 27. 解:(1)CD=BE.理由如下: ∵△ABC和△ADE为等边三角形, ∴AB=AC,AE=AD,∠BAC=∠EAD=60o. ∵∠BAE =∠BAC-∠EAC =60o-∠EAC, ∠DAC =∠DAE-∠EAC =60o-∠EAC, ∴∠BAE=∠DAC, ∴△ABE ≌ △ACD.∴CD=BE. (2)△AMN是等边三角形.理由如下: ∵△ABE ≌ △ACD, ∴∠ABE=∠ACD. ∵M、N分别是BE、CD的中点, ∴BM= ∵AB=AC,∠ABE=∠ACD, ∴△ABM ≌ △ACN. ∴AM=AN,∠MAB=∠NAC. ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o. ∴△AMN是等边三角形. (3) 设AD=a,则AB=2a. ∵AD=AE=DE,AB=AC, ∴CE=DE. ∵△ADE为等边三角形,∴∠DEC=120 o, ∠ADE=60o, ∴∠EDC=∠ECD=30o, ∴∠ADC=90o. ∴在Rt△ADC中,AD=a,∠ACD=30 o , ∴ CD= ∵N为DC中点, ∴ ∵△ADE,△ABC,△AMN为等边三角形, ∴S△ADE∶S△ABC∶ S△AMN 解法二:(2)△AMN是等边三角形.理由如下: ∵△ABE ≌ △ACD,M、N分别是BE、CN的中点,∴AM=AN,NC=MB. ∵AB=AC,∴△ABM ≌ △ACN,∴∠MAB=∠NAC, ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o. ∴△AMN是等边三角形 (3)设AD=a,则AD=AE=DE= a,AB=BC=AC=2a. 易证BE⊥AC,∴BE= ∴ ∵△ADE,△ABC,△AMN为等边三角形, ∴S△ADE∶S△ABC∶ S△AM N (责任编辑:admin) |
