|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况，在查看时请点击右上角全屏查看 2018年玉林中考数学冲刺试题 一.选择题 1.﹣  的相反数是（ ） A. 4  B. ﹣ C. D. ﹣42.由6个完全相同的小正方体搭成的几何体如图所示，它的俯视图是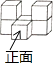（ ）  A.  B.  C.  D.  3.新疆近年旅游业发展快速，每年都吸引众多海内外游客前来观光、旅游，据有关部门统计报道：2016年全疆共接待游客3354万人次，将3354万用科学记数法表示为（ ） A. 3.354×106 B. 3.354×107 C. 3.354×108 D. 33.54×106 4.下列计算正确的是（ ） A. a3﹣a2=a B. a2•a3=a6 C. （2a）2=4a2 D. a6÷a3=a2 5.抛物线y=﹣（a﹣8）2+2的顶点坐标是（ ） A. （ 2，8 ）  B. （ 8，2 ） C. （﹣8，2 ） D. （﹣8，﹣2）6.如图，菱形ABCD的两条对角线相交于点O，若AC=6，BD=4，则菱形ABCD的周长是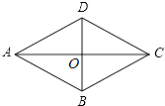（ ）  A. 24 B. 16 C. 2  D. 4  7.若关于x的一元二次方程kx2﹣4x+3=0有实数根，则k的非负整数值是（ ） A. 1 B. 0，1 C. 1，2 D. 1，2，38.如图，直线AB与半径为2的⊙O相切于点C，点D，E，F是⊙O上三个点，EF∥AB，若EF=2 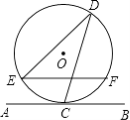，则∠EDC的度数为（ ） A. 60° B. 90° C. 30° D. 75° 9.某工程队准备修建一条长1200m的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快20%，结果提前2天完成任务．若设原计划每天修建道路x m，则根据题意可列方程为（ ） A.  ﹣  =2 B.  ﹣ =2C. ﹣ =2 D. ﹣ =210.如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为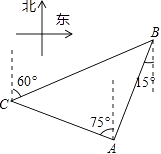（ ）  A. 20海里 B. 10 海里 C. 20  海里 D. 30海里11.如果一个正比例函数的图象经过不同象限的两点A（2，m），B（n，3），那么一定有（ ） A. m＞0，n＞0 B. m＞0，n＜0 C. m＜0，n＞0 D. m＜0，n＜012.如图，平行四边形ABCD的顶点C在y轴正半轴上，CD平行于x轴，直线AC交x轴于点E，BC⊥AC，连接BE，反比例函数 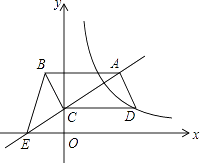 （x＞0）的图象经过点D．已知S△BCE=2，则k的值是（ ） A. 2  B. ﹣2 C. 3 D. 4二.填空题 13.分解因式：xy2﹣x=________． 14.若一个多边形内角和为900°，则这个多边形是________边形． 15.函数y=  中自变量x的取值范围是________． 16.如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为点M，若∠1=58°，则∠2=________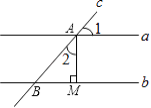．  17.如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y= 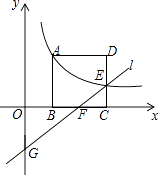 （k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，  ），过点E的直线l交x轴于点F，交y轴于点G（0，﹣2），则点F的坐标是________． 18.如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2 ， 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 ， 以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是________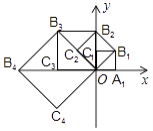．  三.解答题 19.计算：  ． 20.先化简，再求值：  ÷（m﹣1﹣  ），其中m= ． 21.已知：如图，在△ABC中，∠A=30°，∠B=60°．  (1)作∠B的平分线BD，交AC于点D；作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）； (2)连接DE，求证：△ADE≌△BDE． 22.某校实施新课程改革以来，学生的学习能力有了很大提高．王老师为进一步了解本班学生自主学习、合作交流的现状，对该班部分学生进行调查，把调查结果分为四类（A．特别好，B．好，C．一般，D．较差）后，再将调查结果绘制成两幅不完整的统计图（如图）．请根据统计图解答下列问题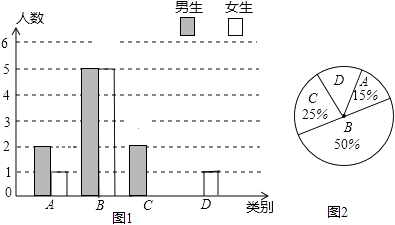：  (1)本次调查中，王老师一共调查了________名学生； (2)将两幅统计图中不完整的部分补充完整； (3)假定全校各班实施新课程改革效果一样，全校共有学生2 400人，请估计该校新课程改革效果达到A类的有多少学生； (4)为了共同进步，王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习，请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率． 23.如图，PA、PB分别与⊙O相切于点A、B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N．  (1)求证：OM=AN； (2)若⊙O的半径R=3，PA=9，求OM的长． 24.某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量yA（千克）与时间x（时）的函数图象，线段EF表示B种机器人的搬运量yB（千克）与时间x（时）的函数图象．根据图象提供的信息，解答下列问题：  (1)求yB关于x的函数解析式； (2)如果A、B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？ 25.如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．  (1)求证：四边形EFDG是菱形； (2)求证：EG2=  AF•GF； (3)若AG=6，EG=2  ，求BE的长． 26.如图1，抛物线y=﹣x2+2x+3与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C．  (1)直接写出A，B，C三点的坐标和抛物线的对称轴； (2)如图2，连接BC，与抛物线的对称轴交于点E，点P位线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；用含m的代数式表示线段PF的长；并求出当m为何值时，四边形PEDF为平行四边形？ (3)如图3，连接AC，在x轴上是否存在点Q，使△ACQ为等腰三角形，若存在，请求出点Q的坐标，若不存在，请说明理由． 2018年玉林中考数学冲刺试题参考答案 一.选择题 1.【答案】C 【考点】相反数 【解析】【解答】﹣ 的相反数是 ，故答案为：C． 【分析】根据相反数的定义只有符号相反两个数是互为相反数，即可得到答案. 2.【答案】C 【考点】简单组合体的三视图 【解析】【解答】俯视图从左到右分别是1，2，1个正方形． 故答案为：C． 【分析】根据几何体的三视图的定义，由三视图的形状来判定即可. 3.【答案】B 【考点】科学记数法—表示绝对值较大的数 【解析】【解答】解：将3354万用科学记数法表示为：3.354×107 ． 故答案为：B． 【分析】根据科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数，依此方法即可判别. 4.【答案】C 【考点】有理数的乘法，有理数的乘方，有理数的除法 【解析】【解答】解：A、a3﹣a2不是同类项不能合并，A不符合题意； B、a2•a3=a5 ， B不符合题意； C、（2a）2=4a2 ， C符合题意； D、a6÷a3=a3 ， D不符合题意； 故答案为：C． 【分析】根据有理数的运算法则分别进行计算即可得到结论. 5.【答案】B 【考点】二次函数的性质 【解析】【解答】抛物线y=﹣（a﹣8）2+2的顶点坐标是（8，2）． 故答案为：B． 【分析】由二次函数的顶点式y=﹣（a﹣8）2+2直接进行判别即可得到. 6.【答案】D 【考点】菱形的性质 【解析】【解答】菱形对角线互相垂直平分， ∴BO=OD=2，AO=OC=3， ∴AB=  = ，∴菱形的周长为4 ．故答案为：D． 【分析】根据菱形的性质得到BO=OD=2，AO=OC=3，再由勾股定理得到AB长度，即可得到菱形的周长. 7.【答案】A 【考点】一元二次方程的定义，根的判别式 【解析】【解答】根据题意得：△=16﹣12k≥0，且k≠0， 解得：k≤  ，则k的非负整数值为1或0． ∵k≠0， ∴k=1． 故答案为：A． 【分析】先根据题意由根判别式得到k的取值范围，再非负性得到k的取值范围. 8.【答案】C 【考点】切线的性质 【解析】【解答】连接OC，与EF交于点G，再连接OE，  ∵AB为圆O的切线， ∴OC⊥AB， ∵EF∥AB， ∴OC⊥EF， ∴EG=FG= EF= ，在Rt△OEG中，OE=2，EG= ，根据勾股定理得：OG=1， ∴∠OEG=30°， ∴∠EOG=60°， ∵∠EDC与∠EOC都对  ，则∠EDC=30°． 故答案为：C. 【分析】先根据切线的性质得到EG，再勾股定理得到OG=1，再由直角三角形性质得到∠EOG=60°，即可得到∠EDC的度数. 9.【答案】D 【考点】由实际问题抽象出分式方程 【解析】【解答】设原计划每天修建道路x m，则实际每天修建道路为（1+20%）x m， 由题意得， ﹣ =2．故答案为：D． 【分析】根据已知条件设原计划每天修建道路x m，则实际每天修建道路为（1+20%）x m，根据采用新的施工方式，提前2天完成任务，列出分式方程即可． 10.【答案】C 【考点】解直角三角形的应用-方向角问题 【解析】【解答】如图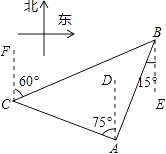，  ∵∠ABE=15°，∠DAB=∠ABE， ∴∠DAB=15°， ∴∠CAB=∠CAD+∠DAB=90°． 又∵∠FCB=60°，∠CBE=∠FCB，∠CBA+∠ABE=∠CBE， ∴∠CBA=45°． ∴在直角△ABC中，sin∠ABC=  =  =  ，∴BC=20 海里．故答案为：C． 【分析】本题考查了解直角三角形的应用-方向角问题，根据题意易求△ABC是等腰直角三角形，通过解该直角三角形来求BC的长度即可得到答案． 11.【答案】D 【考点】正比例函数的图象和性质 【解析】【解答】A、m＞0，n＞0，A、B两点在同一象限，A不符合题意； B、m＞0，n＜0，A、B两点不在同一个正比例函数，B不符合题意； C、m＜0，n＞0，A、B两点不在同一个正比例函数，C不符合题意； D、m＜0，n＜0，A、B两点在同一个正比例函数的不同象限，D符合题意. 故答案为：D． 【分析】本题考查的是一次函数图象上点的坐标特点，根据正比例函数图象所在象限，可判断出m、n的符号即可． 12.【答案】D 【考点】平行四边形的性质，相似三角形的判定与性质，反比例函数图象上点的坐标特征 【解析】【解答】设D点坐标为（m，n），则AB=CD=m， ∵CD平行于x轴，AB∥CD， ∴∠BAC=∠CEO． ∵BC⊥AC，∠COE=90°， ∴∠BCA=∠COE=90°， ∴△ABC∽△ECO， ∴  =  ，∴BC•EC=AB•CO=mn． ∵点D在反比例函数y= 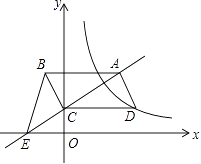 的图象上， ∴k=mn=BC•EC=2S△BCE=4． 故答案为：D． 【分析】由反比例函数的和图象特征得，∠BAC=∠CEO，从而得到△ABC∽△ECO，再由相似三角形的性质即可得k的值. 二.填空题 13.【答案】x（y﹣1）（y+1） 【考点】提公因式法与公式法的综合运用 【解析】【解答】解：xy2﹣x， =x（y2﹣1）， =x（y﹣1）（y+1）． 故答案为：x（y﹣1）（y+1）． 【分析】先提取公因式，再应用平方差公式即可因式分解. 14.【答案】七 【考点】多边形内角与外角 【解析】【解答】解：设这个多边形是n边形，根据题意得， （n﹣2）•180°=900°， 解得n=7． 故答案为：七． 【分析】根据多边形的内角和定理进行计算，即可得到多边形的边数. 15.【答案】x＞3 【考点】分式有意义的条件，二次根式有意义的条件，函数自变量的取值范围 【解析】【解答】解：根据题意得：x﹣3＞0， 解得：x＞3． 【分析】先根据二次根式有意义的条件得到x的取值范围，再由分式有意义和条件即可判别. 16.【答案】32° 【考点】平行线的性质 【解析】【解答】解：∵直线a∥b，AM⊥b， ∴AM⊥a（在同一平面内，垂直于两条平行线中的一条，那么必定垂直于另一条）； ∴∠2=180°﹣90°﹣∠1； ∵∠1=58°， ∴∠2=32°． 故答案是：32°． 【分析】先平行线的性质得到AM⊥a，再由三角形的内角定理即可得到则∠2的值. 17.【答案】（  ，0） 【考点】反比例函数与一次函数的交点问题 【解析】【解答】解：∵正方形的顶点A（m，2）， ∴正方形的边长为2， ∴BC=2， 而点E（n， ），∴n=2+m，即E点坐标为（2+m， ），∴k=2•m= （2+m），解得m=1，∴E点坐标为（3， ），设直线GF的解析式为y=ax+b， 把E（3， ），G（0，﹣2）代入得  ，解得  ，∴直线GF的解析式为y=  x﹣2，当y=0时， x﹣2=0，解得x= ，∴点F的坐标为（ ，0）．【分析】先根据正方形的性质得到BC=2求得点E的坐标，再待定系数法求得直线的解析式即可得到点F的坐标. 18.【答案】（21008 ， 0） 【考点】坐标确定位置，正方形的性质 【解析】【解答】解：∵正方形OA1B1C1边长为1， ∴OB1= ，∵正方形OB1B2C2是正方形OA1B1C1的对角线OB1为边， ∴OB2=2， ∴B2点坐标为（0，2）， 同理可知OB3=2 ，∴B3点坐标为（﹣2，2）， 同理可知OB4=4，B4点坐标为（﹣4，0）， B5点坐标为（﹣4，﹣4），B6点坐标为（0，﹣8）， B7（8，﹣8），B8（16，0） B9（16，16），B10（0，32）， 由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的 倍，∵2016÷8=252 ∴B2016的纵横坐标符号与点B8的相同，横坐标为正值，纵坐标是0， ∴B2016的坐标为（21008 ， 0）． 故答案为：（21008 ， 0）． 【分析】本题主要考查正方形的性质和坐标与图形的性质的知识点，首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标，找出这些坐标的之间的规律，然后根据规律计算即可得到所滶结论． 三.解答题 19.【答案】解： =2 ﹣1﹣4×  +2=1 【考点】实数的运算，零指数幂，特殊角的三角函数值 【解析】【分析】根据实数的运算法则，应用零指数幂，特殊角的三角函数值进行计算即可得到所求结论. 20.【答案】解：原式=  •  = •  =  ，当m= 时，原式=  【考点】分式的化简求值 【解析】【分析】先根据分式的计算方法把分式化简，再把m的值代入即可求出分式的值. 21.【答案】（1）解：作出∠B的平分线BD；作出AB的中点E．如图所示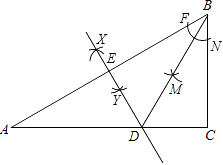：  （2）解：证明： ∵∠ABD= ×60°=30°，∠A=30°，∴∠ABD=∠A， ∴AD=BD， 在△ADE和△BDE中  ∴△ADE≌△BDE（SSS）． 【考点】全等三角形的判定，作图—复杂作图 【解析】【分析】（1）根据尺规作图的方法和步骤进行作图即可得到所作的图形. （2）首先根据角平分线的性质可得得到∠ABD=∠A，再可利用SSS证明△ADE≌△BDE即可得到结论. 22.【答案】（1）20 （2）解：如图所示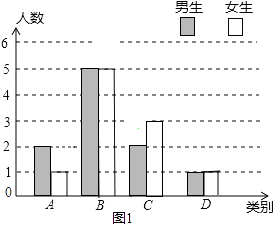：  （3）解：2 400×15%=360（人） （4）解：列表如下：A类中的两名男生分别记为A1和A2．
共有6种等可能的结果，其中，一男一女的有3种，所以所选两位同学恰好是一位男生和一位女生的概率为P=  = 【考点】用样本估计总体，扇形统计图，条形统计图，列表法与树状图法 【解析】【分析】（1）由题意可得由特别好的人数除以占总人数的百分即可得到王老师一共调查学生； （2）由题意可得：C类女生人数；D类男生人数，由（1）（2）继而可补全条形统计图； （3）由样本中A类所占的百分比，即可估计该校新课程改革效果达到A类的有多少学生； （4）首先根据题意列出表格，再利用表格求得所有等可能的结果与恰好选中一名男生和一名女生的情况，继而求得到结论． 23.【答案】（1）证明：如图，连接OA，则OA⊥AP，  ∵MN⊥AP， ∴MN∥OA， ∵OM∥AP， ∴四边形ANMO是矩形， ∴OM=AN （2）解：连接OB，则OB⊥BP ∵OA=MN，OA=OB，OM∥AP． ∴OB=MN，∠OMB=∠NPM． ∴Rt△OBM≌Rt△MNP， ∴OM=MP． 设OM=x，则NP=9﹣x， 在Rt△MNP中，有x2=32+（9﹣x）2 ∴x=5，即OM=5 【考点】全等三角形的判定与性质，勾股定理，矩形的判定与性质，切线的性质 【解析】【分析】（1）先通过作辅助线证明四边形ANMO是矩形再由即矩形性质可解决问题； （2）先证明Rt△OBM≌Rt△MNP得到 OM=MP，再设OM=x，则NP=9-x，由勾股定理列方程再方程即可. 24.【答案】（1）解：设yB关于x的函数解析式为yB=kx+b（k≠0）． 将点（1，0）、（3，180）代入得：  ，解得：k=90，b=﹣90． 所以yB关于x的函数解析式为yB=90x﹣90（1≤x≤6） （2）解：设yA关于x的解析式为yA=k1x． 根据题意得：3k1=180． 解得：k1=60． 所以yA=60x． 当x=5时，yA=60×5=300（千克）； x=6时，yB=90×6﹣90=450（千克）． 450﹣300=150（千克）． 答：如果A、B两种机器人各连续搬运5小时，B种机器人比A种机器人多搬运了150千克． 【考点】一次函数的应用 【解析】【分析】（1）设yB关于x的函数解析式为yB=kx+b（k≠0），再待定系数法可求得函数的解析式； （2）设yA关于x的解析式为yA=k1x．待定系数法求得yA关于x的解析式，然后将x=6，x=5代入一次函数和正比例函数的解析式求得yA ， yB的值，最后求得yA与yB的差即可得到答案． 25.【答案】（1）证明：∵GE∥DF， ∴∠EGF=∠DFG． ∵由翻折的性质可知：GD=GE，DF=EF，∠DGF=∠EGF， ∴∠DGF=∠DFG． ∴GD=DF． ∴DG=GE=DF=EF． ∴四边形EFDG为菱形 （2）证明：如图1所示：连接DE，交AF于点O．  ∵四边形EFDG为菱形， ∴GF⊥DE，OG=OF= GF．∵∠DOF=∠ADF=90°，∠OFD=∠DFA， ∴△DOF∽△ADF． ∴  =  ，即DF2=FO•AF．∵FO= GF，DF=EG，∴EG2= GF•AF（3）如图2所示：过点G作GH⊥DC，垂足为H．  ∵EG2= GF•AF，AG=6，EG=2 ，∴20= FG（FG+6），整理得：FG2+6FG﹣40=0．解得：FG=4，FG=﹣10（舍去）． ∵DF=GE=2 ，AF=10，∴AD=  =4 ．∵GH⊥DC，AD⊥DC， ∴GH∥AD． ∴△FGH∽△FAD． ∴  =  ，即  =  ．∴GH=  ．∴BE=AD﹣GH=4 ﹣ =  【考点】勾股定理，菱形的判定与性质，矩形的性质 【解析】【分析】（1）先依据翻折的性质和平行线的性质证明∠DGF=∠DFG，从而得到GD=DF，接下来依据翻折的性质可证明DG=GE=DF=EF即可得到四边形EFDG为菱形； （2）连接DE，交AF于点O．由菱形的性质可知GF⊥DE，OG=OF= GF，接下来，由△DOF∽△ADF，根据相似三角形的性质可证明DF2=FO•AF，于是可得到EG2= GF•AF；（3）过点G作GH⊥DC，垂足为H．利用（2）的结论可求得FG=4，然后再△ADF中依据勾股定理可求得AD的长，然后再证明△FGH∽△FAD，利用相似三角形的性质可求得GH的长，最后依据BE=AD-GH求解即可BE的长． 26.【答案】（1）解：当y=0时，﹣x2+2x+3=0，解得x1=﹣1，x2=3，则A（﹣1，0），B（3，0）， 当x=0时，y=﹣x2+2x+3=3，则C（0，3）； 抛物线的对称轴是直线x=  =1（2）解：设直线BC的函数关系式为y=kx+b， 把B（3，0），C（0，3）分别代入得  ，解得k=﹣1，b=3，∴直线BC的函数关系式为y=﹣x+3， ∵对称轴是直线x=1， ∴E（1，2）， ∵y=﹣x2+2x+3=﹣（x﹣1）2+4， ∴顶点D的坐标为（1，4）， 当x=m 时，y=﹣m+3， ∴P（m，﹣m+3），F（m，﹣m2+2m+3）， ∴线段DE=4﹣2=2，线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m； ∵PF∥DE， ∴当PF=ED时，四边形PEDF为平行四边形，即﹣m2+3m=2，解得m1=2，m2=1（不合题意，舍去）， ∴当m=2时，四边形PEDF为平行四边形 （3）解：设在x轴上存在点Q（x，0），使△ACQ为等腰三角形．分三种情况： ①如果QA=QC，那么（x+1）2=x2+32 ， 解得x=4， 则点Q1（4，0）； ②如果CA=CQ，那么12+32=x2+32 ， 解得x1=1，x2=﹣1（不合题意舍去）， 则点Q2（1，0）； ③如果AC=AQ，那么12+32=（x+1）2 ， 解得x1=  ﹣1，x2=﹣ ﹣1，则点Q3（ ﹣1，0），Q4（﹣ ﹣1，0）；综上所述存在点Q，使△ACQ为等腰三角形．它的坐标为：Q1（4，0），Q2（1，0），Q3（ ﹣1，0），Q4（﹣ ﹣1，0）． 【考点】坐标确定位置，待定系数法求一次函数解析式，平行四边形的判定，一次函数的性质 【解析】【分析】（1）通过解方程-x2+2x+3=0可得A点和B点坐标，再计算自变量为0时的函数值可得到C点坐标，然后利用对称性可确定抛物线的对称轴； （2）先利用待定系数法求出直线BC的函数关系式为y=-x+3，再确定E（1，2），D（1，4），表示出P（m，-m+3），F（m，-m2+2m+3），接着计算出DE=2，PF=-m2+3m，然后利用平行四边形的判定方法得到-m2+3m=2，再解方程求出m即可． （3）分三种情况：QA=QC；CA=CQ；AC=AQ；进行讨论即可求解． (责任编辑：admin) |