|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况，在查看时请点击右上角全屏查看 2018年钦州中考数学冲刺试题 （考试时间：120分钟 满分120分）
 一.填空：（每小题2分，共20分）1．计算：(－1) ×（－2） = ． 2．如图，已知AB∥CD，则∠A = 度． 3．分解因式 x3－xy2= 。 4．在函数  中，自变量x的取值范围是 。 5．截至2009年6月5日止，全球感染H1N1流感病毒有21240人，感染人数用科学计数法表示为 人．6．方程2 x2－18=0的解是 ． 7．若100个产品中有95个正品、5个次品，从中随机抽取一个， 恰好是次品的概率是 ． 8．某蔬菜基地的圆弧形蔬菜大棚的剖面如图（2）所示，已知 AB＝16m，半径OA＝10m，则中间柱CD的高度为 m． 9．一个扇形所在圆的半径为3cm，扇形的圆心角为120°，则扇形的面积 是 cm2． （结果保留  ）10．如图，是用火柴棍摆成的边长分别是1，2，3 根火柴棍时的正方形．当边长为n根火柴棍时，设摆出的正方形所用的火柴棍的根数为 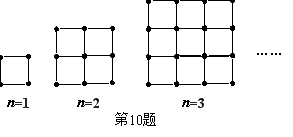 ，则 ＝ ． （用n的代数式表示 ） 二、选择题（每小题3分，共24分） 11．－8的相反数是（ ） A． 8 B．－8 C．  D． 12．已知两圆的半径分别为2和3，圆心距为5，则这两圆的位置关系是（ ）． A.外离 B. 相交 C.外切 D.内切 13．下列四边形：①正方形、②矩形、③菱形，对角线一定相等的是（ ） A．①②③ B．①② C．①③ D．②③ 14．在一次射击测试中，甲、乙、丙、丁的平均环数均相同，而方差分别为8.7，9.1，6.5，7.7，则这四人中，射击成绩最稳定的是（ ） A．甲 B．乙 C．丙 D．丁 15、tan30°的值等于（ ） A.  B.  C.  D.  16图1中几何体的主视图是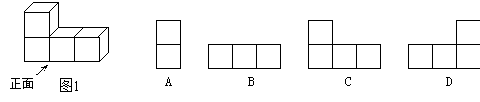（ ）  17．若分式的值为零，则x的值是（ ） A．1 B．0 C．－1 D．±1  18．如图，抛物线y＝ax2＋bx＋c的对称轴是x＝，小亮通过观察得出了下面四条信息： ①c＜0，②abc＜0，③a－b＋c＞0，④2a－3b＝0． 你认为其中正确的有（ ） A．1个 B．2个 C．3个 D．4 三、解答题：(共76分) 19、（本题7分）计算:  20、（本题7分）解方程：  21．（本题8分）如图，E是正方形ABCD的边DC上的一点，过A作AF⊥AE，交CB延长线于点F，求证：△ADE≌△ABF.  22．（本题10分）已知  在平面直角坐标系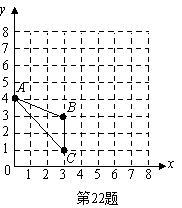中的位置如图10所示．（1）分别写出图中点  的坐标； （2）画出绕点 按顺时针方向旋转 ；（3）求点  旋转到点 所经过的路线长（结果保留 ）．23、（本题10分）右边下面两图是根据某校初三（1）班同学的上学方式情况调查所制作的条形和扇形统计图，请你根据图中提供的信息,解答以下问题： (1) 求该班学生骑自行车的人数有 （2）求该班学生人数 人．  并将条形统计图补充完整；（3）若该校初三年有600名学生， 试估计该年级乘车上学的人数. 24．（本题10分）某冰箱厂为响应国家“家电下乡”号召，计划生产  、 两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于 47500元，不高于48000元，两种型号的冰箱生产成本和售价如下表：
（1）冰箱厂有哪几种生产方案？ （2）该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？ 25、（本题12分）如图5，在 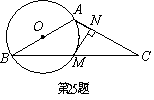 中， ，以 为直径的 交 于点 ， 于点 ．（1）求证  是的切线；（2）若  ，求以直径AB，弦BC和围成图形的面积（结果保留）． 、 26．（本题12分）如图，抛物线  与 轴交于 两点，与 轴交于 点．（1）求  三点的坐标；（2）证明  为直角三角形； （3）在抛物线上除点外，是否还存在另外一个点 ，使 是直角三角形，若存在，请求出点的坐标，若不存在，请说明理由．2018年钦州中考数学冲刺试题参考答案 一．1．2 2．120 3．x（x＋y）（x－y）4．ｘ≥  5．2.124×104 6．3和－3 7． 8．4 9．3 10．2ｎ（ｎ＋1）二．11. A 12.C 13.B 14. C 15. D 16.D 17.A18.B19．2+  20．X1=3，X2=1 21．证明：∵ABCD是正方形 ∴   ∵AF⊥AE ∴  ．在 和 中 ∵  ∴△ADE≌△ABF22．解：（1）  、 （2）图略（3）  ， =  23．解：（1）8 (2）该班学生人数为  （人） 图画对（略）（3）该年级乘车上学的人数约为  24．. 解：（1）设生产  型冰箱 台，则 型冰箱为 台，由题意得： 解得：   是正整 ∴x取38，39或40．有以下三种生产方案：
（2）设投入成本为  元，由题意有：   ∴y随 的增大而减小∴当 时， 有最小值．即生产  型冰箱40台， 型冰箱50台，该厂投入成本最少此时，政府需补贴给农民  25．（1）证明：连接  ．∵  ，∴ ，∵ ，∴ ．∴  ，∴ ．又  ，∴ ，点 在 上，∴ 是的切线（2）S=  26．解：（1）  抛物线 与轴交于 两点， ．即 ．解之得： ．∴点  的坐标为 ，将 代入 ，得 点的坐标为（0，2）（2）  ， ，则 ， 是直角三角形．（3）将  代入，得  ． 点坐标为 ．7 (责任编辑：admin) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||