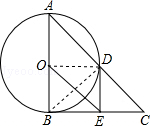
|
☆☆☆ 点击下载试题 ☆☆☆  此试题可能存在乱码情况，在查看时请点击右上角全屏查看 2018年柳州中考数学模拟试题 说明：本试卷共八大题，满分120分，考试时间120分钟 一、选择题（本大题共12小题，每小题3分，共36分。每小题都给出代号为A、B、C、D的四个结论，其中只有一个正确，请考生用2B铅笔在答题卷上将选定的答案标号涂黑）。 1．  的立方根是：A.  B.  C.  D.  2．下列几何体中，俯视图是三角形的是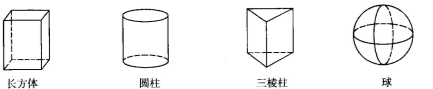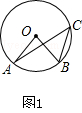：   A. B. C. D. 3. 如图1，A、B、C三点在⊙O上，且∠AOB=80°，则∠ACB等于: A．100° B．80° C．50° D．40° 4. 下列计算正确的是： A.  B.  C.  D.  5．不等式2  -6<0的解集是：A.  ＞3 B. ＜3 C. ＞-3 D. ＜-36．下列图形：①平行四边形；②正方形；③菱形；④矩形；⑤圆. 既是轴对称图形又是中心对称图形的有： A. 1个 B. 2个 C. 3个 D. 4个 7. 若反比例函数  的图象过点(－2，1)，则一次函数 的图象过：A．第一、二、四象限 B．第一、三、四象限 C．第二、三、四象限 D．第一、二、三象限 8．在不透明袋子中装有红、绿小球各一个，除颜色外无其他差别.随机摸出一个小球后，放回并摇匀，再随机摸出一个.两次都摸到相同颜色小球的概率是： A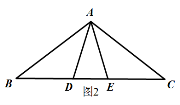．  B． C． D．  9. 如图2，点D、E在△ABC的边BC上，AB=AC，∠BAD=∠DAE=∠EAC=36°，则图中的等腰三角形有： A. 4个 B. 5个 C. 6个 D. 7个 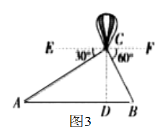 10. 如图3，从热气球C上测定建筑物A、B底部的俯角分别是30°和60°，如果这时气球的高度CD为150米，且点A、D、B在同一直线上，则建筑物A、B间的距离为： A.  B.  C. D.  11. 一个圆锥的侧面展开图形是半径为8cm圆心角为120°的扇形，则此圆锥的底面半径为: A．  cm B． cm C．3cm D． cm12．下列说法错误的是： A．在二次函数  中,当 ＞0时， 随 的增大而增大.B．在二次函数  中,当 =0时,  有最大值为0.C．二次函数的图象  越大图象开口越小,  越小图象开口越大.D．不论 是正数还是负数，抛物线 (≠0)的顶点一定是坐标原点.二、填空题：本大题共6题，每小题3分，共18分。 13. 因式分解：  的结果是 ．14．已知∠A与∠B互余，若∠A=70°，则∠B的度数为 ． 15．已知关于  的方程 的一个根为 ，则实数 的值为 ．16．据统计我县今年参加中考的学生约12000人，12000这个数据用科学计数法表示为 ． 17. 一组按规律排列的式子：  ，则第 （ 为正整数）个式子为 ． 18. 如图4，平面直角坐标系中有一平行四边形OABC，对角线AC、BO相交于点D，点C、D 在双曲线 （ ）上，如果平行四边形OABC的面积等于30，则  的值是 ．三、本大题共2小题，每小题6分，共12分。 19．计算：  20．先化简，再求值：  ，其中 四、本大题共2小题，每小题8分，共16分。 21．如图5，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题： （1）画出△ABC关于  轴对称的△A1B1C1，并写出点A1的坐标．（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．   22. 某校在“读书月”活动中，随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图（图6），请你结合图中的信息解答下列问题： （1）这次抽样调查中，一共抽查了多少名学生？ （2）请补全条形统计图； （3）请计算扇形统计图中“文学类”所对应扇形的圆心角的度数；  （4）已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？五、本大题满分8分  23．如图7，在平行四边形ABCD中，O为对角线AC的中点，过点O的直线EF分别交AB、DC于点E、F，连接CE.（1）求证：△AOE≌△COF； （2）若EF⊥AC，△CBE的周长为8， 求平行四边形ABCD的周长. 六、本大题满分10分 24．某校为了丰富学生的校园生活，准备购进一批篮球和足球，其中篮球的单价比足球的单价多40元，用1500元购进的篮球个数与900元购进的足球个数相同。 （1）篮球和足球的单价各是多少元？ （2）该校打算用1000元购买篮球和足球，且恰好用完1000元，问有几种购买方案？ 本题满分10分  25．如图8，以O为圆心AB的长为直径作圆，在⊙O上取一点C，延长AB至点D，连接DC.过点A作⊙O 的切线交DC的延长线于点E，且∠DCB=∠DAC. （1）求证：CD是⊙O的切线； （2）若AD=6，tan∠DCB =  ，求AE的长.八、本大题满分10分 26．如图9，在平面直角坐标系中，二次函数  的图象与 轴交于点A（-1,0）和点B，与 轴交于点C（0，-4）. 点D是直线BC的下方抛物线上的一动点.（1）求这个二次函数的解析式； （2）连接DO、DC得到△ODC，并把△ODC沿直线OC翻折，得到的四边形DOD′C，是否存在点D，使得四边形DOD′C是菱形？若存在请求出点D的坐标若不存在请说明理由. （3）当点D运动到什么位置时，四边形ABDC的面积最大？求出此时四边形的面积. 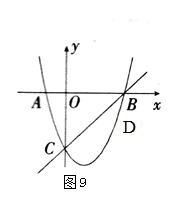 2018年柳州中考数学模拟试题参考答案 一、选择题（每小题3分，共36分）
二、填空题（每小题3分，共18分） 13．x≥3 14．ab(a+1)(a-1) 15．  （若为 扣1分） 16．π 17．2≤x≤6 18．24n﹣5三、（本大题共2小题，每小题6分，共12分） 19. 解：（2015-π）0 —  +2sin30° =1-4+2×  +4 ………………………………（4分）=1+1 ………………………………（5分） =2 ……………………………… （6分） 20.
21.（1）A、B两点的坐标分别为 （－1，0）、（－2，－2）； ………(2分) （2）所画△A1B1C1如图所示； ………(5分) （3）所画点P如图所示， ……………(6分) 5.5 ＜ x ＜8 . ………(8分) 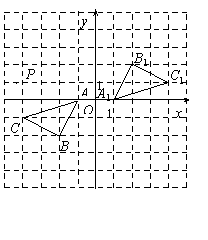 22.解：（1）根据题意得：a =1﹣（35%+25%+25%+10%）=5%；………（2分） （2）根据题意得：（6+19+17+10+8）×35%=21（人），………（4分） 则抽取的样本中，八年级学生睡眠时间在C组的有21人；………(5分) （3）根据题意得：755×  +785×（25%+35%）=453+471=924（人）………（7分）则该校七、八年级学生中睡眠时间合格的共有924人．………（8分） 五、（本大题满分8分） 23.证明：（1）∵AB=AC，D是BC的中点， ∴AD⊥BC………………………………（2分） ∴BE=CE ………………………………（3分） （2）由（1）可知AD⊥BC ∴∠ADC=90° ∴∠EAF+∠C=90°………………………………(4分) ∵∠BAC=45°，BF⊥AF， ∴△ABF为等腰直角三角形， ∴AF=BF………………………………（5分） ∠AFB=90° ∴∠CBF+∠C=90°， ∴∠EAF=∠CBF，………………………………（6分） 在△AEF和△BCF中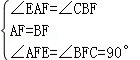，  ，∴△AEF≌△BCF（ASA）………………………………（8分）
(责任编辑：admin) |
||||||||||||||||||||||||||||||||||||
，
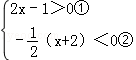……………………………（3分）
BC， 
，即BC2=AC•CD
，
=
………………………………（8分）
）2+
………………………………（5分）
时，PE的最大值为
………………………………（6分）
，0），F4（4﹣
，0）……（10分）
，3），由于直线GF∥AC，因此可设直线GF的解析式为：y=﹣x+h，
，0）。
，0）
