|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况，在查看时请点击右上角全屏查看 2018年郴州中考数学模拟试题 一.选择题 1.﹣  的倒数是（ ） A.  B. ﹣2 C. 2 D. ﹣ 2.如图，已知点A（﹣8，0），B（2，0），点C在直线y=﹣ 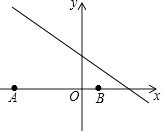 上，则使△ABC是直角三角形的点C的个数为（ ） A. 1  B. 2 C. 3 D. 43.已知等腰三角形的腰和底的长分别是一元二次方程x2﹣6x+8=0的根，则该三角形的周长为（ ） A. 8 B. 10 C. 8或10 D. 124.在一个不透明的盒子中装有12个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球是白球的概率是  ，则黄球的个数为（ ） A. 18 B. 20 C. 24 D. 28 5.如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是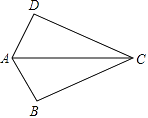（ ）  A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°6.已知两圆半径分别为3、5，圆心距为8，则这两圆的位置关系为（ ） A. 外离 B. 内含 C. 相交 D. 外切 7.如图所示，是由5个相同的小正方体组合而成的几何体，它的左视图是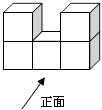（ ）  A.  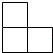B.  C.  D.  8.下列图形中，既是中心对称，又是轴对称图形的是（ ） A. 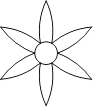 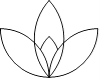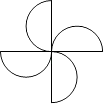B.  C.  D.  9.已知如图，一次函数y=ax+b和反比例函数y=  的图象相交于A、B两点，不等式ax+b＞ 的解集为（ ） A. x＜﹣3 B. ﹣3＜x＜0或x＞1 C. x＜﹣3或x＞1 D. ﹣3＜x＜1 10.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123．其中正确的是（ ）  A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③ 二.填空题 11.20140000用科学记数法表示（保留3个有效数字）为________． 12.已知甲组数据的平均数为  甲 ， 乙组数据的平均数为 乙 ， 且 甲= 乙 ， 而甲组数据的方差为S2甲=1.25，乙组数据的方差为S2乙=3，则________较稳定． 13.点P（﹣2，3）关于x轴对称的点的坐标为________．关于y轴对称的点的坐标为________． 14.在函数y=  中，自变量x的取值范围是________． 15.如图，直线AB∥CD，CA平分∠BCD，若∠1=50°，则∠2=________．  16.如图，AB是⊙O的直径，AB=15，AC=9，则tan∠ADC=________．  17.如图，将矩形纸片ABCD折叠，使边AB、CB均落在对角线BD上，得折痕BE、BF，则∠EBF=________°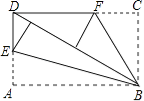．  18.在平面直角坐标系中，对于平面内任一点（m，n），规定以下两种变换： ①f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）； ②g（m，n）=（﹣m，﹣n），如g （2，1）=（﹣2，﹣1） 按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（﹣3，2）]=________． 三.解答题 19.计算：（ ）﹣2+（π﹣2014）0+sin60°+|  ﹣2|． 20.解方程：  ． 21.如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：△CDA≌△CEB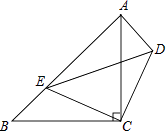．  四.解答题 22.某酒厂每天生产A，B两种品牌的白酒共600瓶，A，B两种品牌的白酒每瓶的成本和利润如下表： 设每天生产A种品牌白酒x瓶，每天获利y元． (1)请写出y关于x的函数关系式； (2)如果该酒厂每天至少投入成本26400元，那么每天至少获利多少元？
23.某调查小组采用简单随机抽样方法，对某市部分中小学生一天中阳光体育运动时间进行了抽样调查，并把所得数据整理后绘制成如下的统计图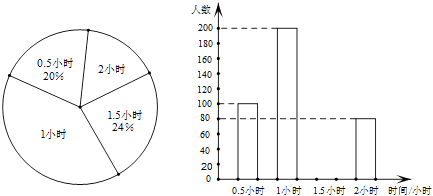：  (1)该调查小组抽取的样本容量是多少？ (2)求样本学生中阳光体育运动时间为1.5小时的人数，并补全占频数分布直方图； (3)请估计该市中小学生一天中阳光体育运动的平均时间． 24.如图，为了测量山顶铁塔AE的高，小明在27m高的楼CD底部D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角36°52′．已知山高BE为56m，楼的底部D与山脚在同一水平线上，求该铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75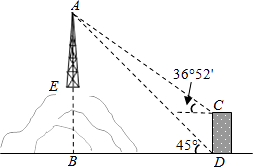）  五.综合题 25.如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE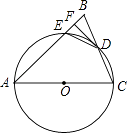．  (1)求证：直线DF与⊙O相切； (2)若AE=7，BC=6，求AC的长． 26.如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（﹣3，0）、B（1，0）、C（0，3）三点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE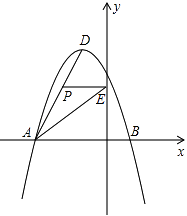．  (1)求抛物线的函数解析式，并写出顶点D的坐标； (2)如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值； (3)在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点P′，求出P′的坐标，并判断P′是否在该抛物线上． 2018年郴州中考数学模拟试题参考答案 一.选择题 1.【答案】B 【考点】倒数 【解析】【解答】﹣ 的倒数是﹣2．故答案为：B． 【分析】根据倒数的定义进行判别，即可得到答案. 2.【答案】C 【考点】一次函数的图象，勾股定理 【解析】【解答】如图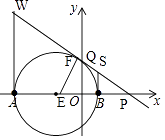，  ①当∠A为直角时，过点A作垂线与直线的交点W（﹣8，10）， ②当∠B为直角时，过点B作垂线与直线的交点S（2，2.5）， ③若∠C为直角 则点C在以线段AB为直径、AB中点E（﹣3，0）为圆心、5为半径的圆与直线y=﹣ 的交点上．在直线y=﹣ 中，当x=0时y=4，即Q（0，4），当y=0时x=  ，即点P（ ，0），则PQ=  =  ，过AB中点E（﹣3，0），作EF⊥直线l于点F， 则∠EFP=∠QOP=90°， ∵∠EPF=∠QPO， ∴△EFP∽△QOP， ∴  =  ，即  =  ，解得：EF=5， ∴以线段AB为直径、E（﹣3，0）为圆心的圆与直线y=﹣ 恰好有一个交点．所以直线y=﹣ 上有一点C满足∠C=90°．综上所述，使△ABC是直角三角形的点C的个数为3， 故答案为：C． 【分析】在解答此题时要分三种情况进行讨论，根据∠A为直角，∠B为直角与∠C为直角三种情况进行分析，即可得到所求结论. 3.【答案】B 【考点】一元二次方程的解，三角形三边关系，勾股定理 【解析】【解答】x2﹣6x+8=0 （x﹣4）（x﹣2）=0 ∴x1=4，x2=2， 由三角形的三边关系可得： 腰长是4，底边是2， 所以周长是：4+4+2=10． 故答案为：B． 【分析】先用因式分解法可以求出方程的两个根分别是4和2，根据等腰三角形的三边关系，腰应该是4，底是2，然后可以求出三角形的周长即可． 4.【答案】C 【考点】概率公式 【解析】【解答】设黄球的个数为x个， 根据题意得：  = ，解得：x=24， 经检验：x=24是原分式方程的解； ∴黄球的个数为24． 故答案为：C． 【分析】设黄球的个数为x个，根据题意列出分式方程，解分式方程即可求出黄球的个数. 5.【答案】C 【考点】全等三角形的判定 【解析】【解答】A、添加CB=CD，根据SSS，能判定△ABC≌△ADC，A不符合题意； B、添加∠BAC=∠DAC，根据SAS，能判定△ABC≌△ADC，B不符合题意； C、添加∠BCA=∠DCA时，不能判定△ABC≌△ADC，C符合题意； D、添加∠B=∠D=90°，根据HL，能判定△ABC≌△ADC，D不符合题意. 故答案为：C． 【分析】由条件可得AC=AC，再结合AB=AD，根据全等三角形的判定方法逐项判断即可得到所求结论． 6.【答案】D 【考点】圆与圆的位置关系 【解析】【解答】∵⊙O1、⊙O2的半径分别是3、5，O1O2=8， 又∵3+5=8， ∴⊙O1和⊙O2的位置关系是外切． 故答案为：D． 【分析】根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系，即可得出两圆的位置关系． 7.【答案】D 【考点】简单组合体的三视图 【解析】【解答】此几何体的左视图是“日”字形． 故答案为：D． 【分析】根据几何体的三视图的定义进行判别，即可得到结论. 8.【答案】A 【考点】轴对称图形，中心对称及中心对称图形 【解析】【解答】解：A、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，A符合题意； B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，B不符合题意； C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，C不符合题意； D、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，D不符合题意. 故答案为：A． 【分析】根据中心对轴和轴对称的定义进行判别即可得到结论. 9.【答案】B 【考点】反比例函数与一次函数的交点问题 【解析】【解答】不等式ax+b＞ 的解集为﹣3＜x＜0或x＞1．故答案为：B． 【分析】通过观察函数图象得到当-3＜x＜0或x＞1时，得到一次函数图象都在反比例函数图象上方，即可得到所求结论. 10.【答案】A 【考点】一次函数的应用 【解析】【解答】甲的速度为：8÷2=4（米/秒）； 乙的速度为：500÷100=5（米/秒）； b=5×100﹣4×（100+2）=92（米）； 5a﹣4×（a+2）=0， 解得a=8， c=100+92÷4=123（秒）， ∴正确的有①②③． 故答案为：A． 【分析】本题是一道一次函数的综合试题，考查了路程=速度×时间的运用，追击问题的运用，由图象可以看出甲2秒跑了8米可以求出甲的速度为4米/秒，b是表示乙跑到终点时甲乙的距离，c表示乙出发后甲到达终点的时间．根据总路程÷速度-甲先走的时间即是c的值，即可得到所求结论． 二.填空题 11.【答案】2.01×107 【考点】科学记数法—表示绝对值较大的数 【解析】【解答】解：20140000=2.014×107≈2.01×107 ． 故答案为：2.01×107 ． 【分析】此题考查科学记数法的表示方法，科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字，即可求出所求的结论． 12.【答案】甲 【考点】方差 【解析】【解答】解：由于甲的方差小于乙的方差，所以甲组数据稳定． 故答案为：甲． 【分析】根据甲，乙方差的大小 来进行判别，即可得到两数据中那组稳定. 13.【答案】（﹣2，﹣3）；（2，3） 【考点】关于x轴、y轴对称的点的坐标 【解析】【解答】解：点P（﹣2，3）关于x轴对称的点的坐标为（﹣2，﹣3）， 关于y轴对称的点的坐标为（2，3）． 故答案为：（﹣2，﹣3）；（2，3）． 【分析】根据关于x轴对称的点的坐标和关于y轴对称的点的坐标的特点进行判别，即可得到答案. 14.【答案】x≥ 【考点】二次根式有意义的条件，函数自变量的取值范围 【解析】【解答】解：根据题意得：2x﹣1≥0， 解得，x≥ ．【分析】根据二次根式有意义的条件，得到关于x的一元一次不等式，再解不等式即可. 15.【答案】65° 【考点】平行线的性质 【解析】【解答】解：∵AB∥CD， ∴∠ABC+∠BCD=180°， 而∠ABC=∠1=50°， ∴∠BCD=130°， ∵CA平分∠BCD， ∴∠ACD= ∠BCD=65°，∵AB∥CD， ∴∠2=∠ACD=65°． 故答案为：65°． 【分析】先由平行线的性质得到∠BCD=130°，再由角平分线的定义得到∠ACD=65°，最后由平行线的性质得到∠2度数. 16.【答案】  【考点】勾股定理，圆周角定理，锐角三角函数的定义 【解析】【解答】解：∵AB为⊙O直径， ∴∠ACB=90°， ∴BC=  =12，∴tan∠ADC=tanB=  =  = ，故答案为： ．【分析】先根据勾股定理求出BC的长，再将tan∠ADC转化为tanB进行计算即得tan∠ADC的值． 17.【答案】45° 【考点】角的计算，翻折变换（折叠问题） 【解析】【解答】解：∵四边形ABCD是矩形， 根据折叠可得∠ABE=∠EBD= ∠ABD，∠DBF=∠FBC= ∠DBC，∵∠ABE+∠EBD+∠DBF+∠FBC=∠ABC=90°， ∴∠EBD+∠DBF=45°， 即∠EBF=45°， 故答案为：45°． 【分析】根据四边形ABCD是矩形，得出∠ABE=∠EBD= ∠ABD，∠DBF=∠FBC=∠DBC，再根据∠ABE+∠EBD+∠DBF+∠FBC=∠ABC=90°，得出∠EBD+∠DBF=45°，从而求出所求的结论． 18.【答案】（3，2） 【考点】点的坐标 【解析】【解答】解：∵f（﹣3，2）=（﹣3，﹣2）， ∴g[f（﹣3，2）]=g（﹣3，﹣2）=（3，2）， 故答案为：（3，2）． 【分析】本题考查了点的坐标，根据f、g的规定进行计算即可得出所求结论． 三.解答题 19.【答案】解：原式=9+1+  +2﹣ =12﹣ ． 【考点】实数的运算，零指数幂，负整数指数幂，特殊角的三角函数值 【解析】【分析】根据零指数幂，负整数指数幂和特殊角的三角函数值进行计算，即可求出结论. 20.【答案】解：方程的两边同乘（x+2）（x﹣2），得 x+2=4， 解得x=2． 检验：把x=2代入（x2﹣4）=0． ∴原方程无解． 【考点】解分式方程 【解析】【分析】根据解分式方程计算法则进行计算即可得到所求结论，注意分式方程必需检根. 21.【答案】证明：∵△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°， ∴CE=CD，BC=AC， ∴∠ACB﹣∠ACE=∠DCE﹣∠ACE， ∴∠ECB=∠DCA， 在△CDA与△CEB中 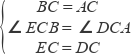 ，∴△CDA≌△CEB． 【考点】全等三角形的判定，等腰直角三角形 【解析】【分析】根据等腰直角三角形的性质得出CE=CD，BC=AC，再利用全等三角形的判定证明即可得到△CDA≌△CEB. 四.解答题 22.【答案】（1）解：A种品牌白酒x瓶，则B种品牌白酒（600﹣x）瓶，依题意，得 y=20x+15（600﹣x）=5x+9000； （2）解：A种品牌白酒x瓶，则B种品牌白酒（600﹣x）瓶，依题意，得 50x+35（600﹣x）≥26400，解得x≥360， ∴每天至少获利y=5x+9000=10800． 【考点】一次函数的应用 【解析】【分析】（1）根据题意，列出y关于x的函数关系式，再进行化简即可求得y关于x的函数关系式； （2）首先根据题意可得不等式：50x+35（600-x）≥26400，解不等式即可求得x的取值范围，又由一次函数性质，即可求得所求结论. 23.【答案】（1）解：由题意可得：0.5小时的人数为：100人，所占比例为：20%， ∴本次调查共抽样了500名学生； （2）解：1.5小时的人数为：500×24%=120（人） 如图所示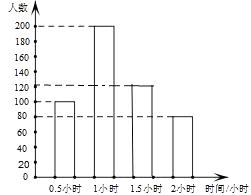：  （3）解：根据题意得：  ，即该市中小学生一天中阳光体育运动的平均时间约1小时． 【考点】频数（率）分布直方图，扇形统计图，加权平均数 【解析】【分析】（1）利用0.5小时的人数为：100人，所占比例为：20%，即可求出样本容量； （2）利用样本容量乘以1.5小时的百分数，即可求出1.5小时的人数，补全占频数分布直方图即可； （3）根据题意计算出该市中小学生一天中阳光体育运动的平均时间即可． 24.【答案】解：如图，过点C作CF⊥AB于点F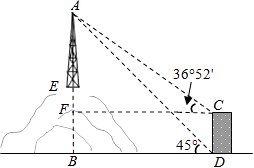．  设塔高AE=x， 由题意得，EF=BE﹣CD=56﹣27=29m，AF=AE+EF=（x+29）m， 在Rt△AFC中，∠ACF=36°52′，AF=（x+29）m， 则CF=  ≈  =  x+  ，在Rt△ABD中，∠ADB=45°，AB=x+56， 则BD=AB=x+56， ∵CF=BD， ∴x+56= x+ ，解得：x=52， 答：该铁塔的高AE为52米． 【考点】解直角三角形的应用 【解析】【分析】设出未知数铁塔高为x ,用x 的代数式表示出AF、BD，在Rt△ABD中利用∠ADB=45°构建方程，求出x. 五.综合题 25.【答案】（1）证明：如图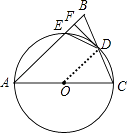，  连接OD． ∵AB=AC， ∴∠B=∠C， ∵OD=OC， ∴∠ODC=∠C， ∴∠ODC=∠B， ∴OD∥AB， ∵DF⊥AB， ∴OD⊥DF， ∵点D在⊙O上， ∴直线DF与⊙O相切； （2）解：∵四边形ACDE是⊙O的内接四边形， ∴∠AED+∠ACD=180°， ∵∠AED+∠BED=180°， ∴∠BED=∠ACD， ∵∠B=∠B， ∴△BED∽△BCA， ∴  =  ，∵OD∥AB，AO=CO， ∴BD=CD= BC=3，又∵AE=7， ∴  =  ，∴BE=2， ∴AC=AB=AE+BE=7+2=9． 【考点】切线的判定，相似三角形的判定与性质 【解析】【分析】（1）连接OD，利用AB=AC，OD=OC，证得OD∥AD，再证明DF⊥OD，即查得到DF为⊙O的切线； （2）四边形ACDE是⊙O的内接四边形，∠BED=∠ACD，∠B=∠B，证得△BED∽△BCA，再由相似三角形的性质求得BE的值，最后即可求得AC的长. 26.【答案】（1）解：∵抛物线y=ax2+bx+c经过A（﹣3，0）、B（1，0）、C（0，3）三点， ∴  ，解得 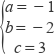 ，∴解析式为y=﹣x2﹣2x+3 ∵﹣x2﹣2x+3=﹣（x+1）2+4， ∴抛物线顶点坐标D为（﹣1，4）． （2）解：∵A（﹣3，0），D（﹣1，4）， ∴设AD为解析式为y=kx+b，有  ，解得  ，∴AD解析式：y=2x+6， ∵P在AD上， ∴P（x，2x+6）， ∴S△APE= •PE•yP= •（﹣x）•（2x+6）=﹣x2﹣3x（﹣3＜x＜﹣1），当x=﹣  =﹣  时，S取最大值  ．（3）解：如图1，设P′F与y轴交于点N，过P′作P′M⊥y轴于点M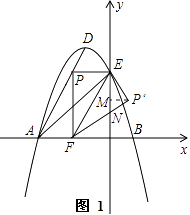，  ∵△PEF沿EF翻折得△P′EF，且P（﹣ ，3），∴∠PFE=∠P′FE，PF=P′F=3，PE=P′E= ，∵PF∥y轴， ∴∠PFE=∠FEN， ∵∠PFE=∠P′FE， ∴∠FEN=∠P′FE， ∴EN=FN， 设EN=m，则FN=m，P′N=3﹣m． 在Rt△P′EN中， ∵（3﹣m）2+（ ）2=m2 ， ∴m=  ．∵S△P′EN= •P′N•P′E= •EN•P′M，∴P′M=  ．在Rt△EMP′中， ∵EM=  =  ，∴OM=EO﹣EM=  ，∴P′（ ， ）．当x= 时，y=﹣（ ）2﹣2• +3=  ≠ ，∴点P′不在该抛物线上． 【考点】二次函数图象与几何变换，二次函数与一次函数的交点问题 【解析】【分析】（1）利用待定系数法把A、B、C三点坐标代入解析式，求出a、b、c即可；（2）由于P在AD上运动，须求出AD的解析式，设出P的横坐标为x,用x的代数式分别表示P的纵坐标、PE长，代入三角形面积公式，构建函数，用配方法求出最值；（3）利用折叠的性质得出对应边相等，设EN=m,用m的代数式分别表示P' 坐标，将横坐标代入解析式，所求出的结果是否等于P'的纵坐标可判断出. (责任编辑：admin) |