|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况，在查看时请点击右上角全屏查看 2018年玉林中考数学模拟试题 一.填空题： 1.若|x+y|+|y﹣3|=0，则x﹣y的值为________． 2.函数y=  的自变量的取值范围是________． 3.一只口袋中放着8只红球和16只黑球，这两种球除颜色以外没有任何其他区别．从口袋中随机取出一个球，取出这个球是红球的概率为________． 4.如图，上体育课，甲、乙两名同学分别站在C、D的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米．甲身高1.8米，乙身高1.5米，则甲的影长是________米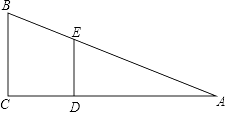．  5.将一个圆分成四个扇形，它们的圆心角的度数比为2：4：5：7，则最大扇形的圆心角是________． 6.观察下列数据：﹣2，  ，﹣  ，  ，﹣  ，…，它们是按一定规律排列的，依照此规律，第11个数据是________． 二.解答题： 7.计算：cos30°  +|1﹣  |﹣（  ）﹣1 ． 8.如图，△ABC中，AB=AC，E、F分别是BC、AC的中点，以AC为斜边作Rt△ADC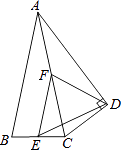．  （1）求证：FE=FD； （2）若∠CAD=∠CAB=24°，求∠EDF的度数． 9.学校举办“大爱镇江”征文活动，小明为此次活动设计了一个以三座山为背景的图标（如图），现用红、黄两种颜色对图标中的A，B，C三块三角形区域分别涂色，一块区域只涂一种颜色．  （1）请用树状图列出所有涂色的可能结果； （2）求这三块三角形区域中所涂颜色是“两块黄色、一块红色”的概率． 10.如图，在矩形ABCD中，AB=8，AD=12，过点A，D两点的⊙O与BC边相切于点E，求⊙O的半径．  11.某市居民用电的电价实行阶梯收费，收费标准如下表：
（1）已知李叔家四月份用电286度，缴纳电费178.76元；五月份用电316度，缴纳电费198.56元，请你根据以上数据，求出表格中a，b的值． （2）六月份是用电高峰期，李叔计划六月份电费支出不超过300元，那么李叔家六月份最多可用电多少度？ 12.张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据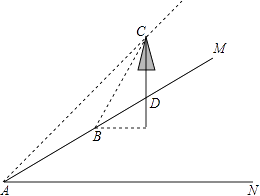： ≈1.732） 13.如图，抛物线m：y=﹣0.25（x+h）2+k与x轴的交点为A，B，与y轴的交点为C，顶点为M（3，6.25），将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为D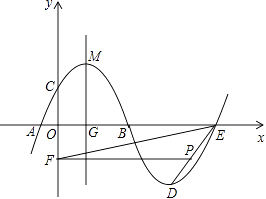．  （1）求抛物线n的解析式； （2）设抛物线n与x轴的另一个交点为E，点P是线段DE上一个动点（P不与D，E重合），过点P作y轴的垂线，垂足为F，连接EF．如果P点的坐标为（x，y），△PEF的面积为S，求S与x的函数关系式，写出自变量x的取值范围，并求出S的最大值； （3）设抛物线m的对称轴与x轴的交点为G，以G为圆心，A，B两点间的距离为直径作⊙G，试判断直线CM与⊙G的位置关系，并说明理由． 2018年玉林中考数学模拟试题参考答案 一.填空题： 1.【答案】﹣6 【考点】解二元一次方程组 【解析】【解答】解：|x+y|+|y﹣3|=0， ∴x+y=0，y﹣3=0，解得y=3，x=﹣3． ∴x﹣y=﹣3﹣3=﹣6． 故答案为：﹣6． 【分析】此题考查的是非负数的性质，几个非负数之和为0，则每一个数都为0，建立方程组  ，求出方程组的解，即可求出x-y的值。 2.【答案】x≥﹣3且x≠﹣1 【考点】分式有意义的条件，二次根式有意义的条件，函数自变量的取值范围 【解析】【解答】解：由题意，得 x+3≥0且x+1≠0， 解得x≥﹣3且x≠﹣1， 故答案为：x≥﹣3且x≠﹣1． 【分析】观察此函数含自变量的式子是分式，且分子中含有二次根式。根据分母≠0，且被开方数≥0，建立不等式组求解即可。 3.【答案】 【考点】概率公式 【解析】【解答】解：∵一只口袋中放着8只红球和16只黑球，这两种球除颜色以外没有任何其他区别， ∴从口袋中随机取出一个球，取出这个球是红球的概率为：  = ．故答案为： ．【分析】由题意可知，一共有24种可能，从口袋中随机取出一个球，取出这个球是红球有8种可能，根据概率公式求解即可。 4.【答案】6 【考点】相似三角形的判定与性质，相似三角形的应用 【解析】【解答】解：设甲的影长是x米， ∵BC⊥AC，ED⊥AC， ∴ED∥BC ∴△ADE∽△ACB， ∴  =  ，∵CD=1m，BC=1.8m，DE=1.5m， ∴  =  ，解得：x=6． 所以甲的影长是6米． 【分析】将实际问题转化为数学问题，由已知易证明ED∥BC，从而得到△ADE∽△ACB，再根据相似三角形的性质对应边成比例，建立方程，解方程即可求解。 5.【答案】140° 【考点】圆心角、弧、弦的关系 【解析】【解答】解：设四个扇形的圆心角的度数是2x，4x，5x，7x， 得出方程2x+4x+5x+7x=360， 解得：x=20， 故7×20°=140°． 故答案为：140° 【分析】将一个圆分成四个扇形，可知道四个圆心角的度数之和为360°，根据它们的圆心角的度数比为2：4：5：7，设未知数建立方程，求解即可知道最大圆心角的度数。 6.【答案】﹣  【考点】探索数与式的规律 【解析】【解答】解：∵﹣2=﹣  ， ，﹣ ， ，﹣ ，…，∴第11个数据是：﹣  =﹣ ．故答案为：﹣ ．【分析】观察此组数据可知，所有数据的分母是连续的正整数，第奇数个是负数，分子是连续正整数的平方加1，根据此规律就可以求出第11个数。 二.解答题： 7.【答案】解：原式=  +  + ﹣1﹣3=2 ﹣  【考点】实数的运算，负整数指数幂，特殊角的三角函数值 【解析】【分析】此题是一道综合计算题，在解答此题时注意：|1﹣ |=-1，（ ）﹣1 ． =3。 8.【答案】（1）证明：∵E、F分别是BC、AC的中点， ∴FE=  AB，∵F是AC的中点，∠ADC=90°， ∴FD= AC，∵AB=AC， ∴FE=FD； （2）解：∵E、F分别是BC、AC的中点， ∴FE∥AB， ∴∠EFC=∠BAC=24°， ∵F是AC的中点，∠ADC=90°， ∴FD=AF． ∴∠ADF=∠DAF=24°， ∴∠DFC=48°， ∴∠EFD=72°， ∵FE=FD， ∴∠FED=∠EDF=54°． 【考点】三角形的外角性质，等腰三角形的性质，直角三角形斜边上的中线，三角形中位线定理 【解析】【分析】（1）由已知易证FD是△ABC的中位线和△Rt△ACD斜边上的中线，根据三角形中位线定理及直角三角形斜边上的中线等于斜边的一半，易证得FE=FD。 （2）由已知条件得出FE∥AB，求出∠EFC的度数，根据直角三角形斜边上的中线等于斜边的一半，就可以求出∠ADF=∠DAF，再根据三角形的外角等于不相邻的两内角之和，求出∠DFC的度数，利用（1）的结论，就可以求出∠EDF的度数。 9.【答案】（1）解：画树状图法如下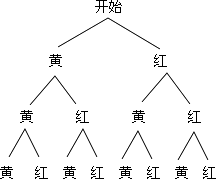：  所有可能为：（黄，黄，黄），（黄，黄，红），（黄，红，黄），（黄，红，红），（红，黄，黄）， （红，黄，红），（红，红，黄），（红，红，红） （2）解：从树状图看出，所有可能出现的结果共有8种， 恰好“两块黄色、一块红色”的结果有3种， 所以这个事件的概率是  ． 【考点】列表法与树状图法 【解析】【分析】（1）画出树状图即可。 （2）根据（1）中所画出的树状图求出所有可能的情况数，以及恰好“两块黄色、一块红色恰好”的情况数，然后根据概率公式就可以求出结果。 10.【答案】解：连接OE，并反向延长交AD于点F，连接OA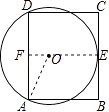，  ∵BC是切线， ∴OE⊥BC， ∴∠OEC=90°， ∵四边形ABCD是矩形， ∴∠C=∠D=90°， ∴四边形CDFE是矩形， ∴EF=CD=AB=8，OF⊥AD， ∴AF= AD= ×12=6，设⊙O的半径为x，则OE=EF﹣OE=8﹣x， 在Rt△OAF中，OF2+AF2=OA2 ， 则（8﹣x）2+36=x2 ， 解得：x=6.25， ∴⊙O的半径为：6.25． 【考点】菱形的判定与性质，垂径定理，切线的性质 【解析】【分析】由已知条件⊙O与BC边相切于点E，连接OE，并反向延长交AD于点F，连接OA。易得到四边形CDFE是矩形，得出OF⊥AD，根据垂径定理求出AF的长，就将求圆的半径转化到Rt△AOF中求解。 11.【答案】（1）解：根据题意得：  ，解得：  （2）解：设李叔家六月份最多可用电x度， 根据题意得：200×0.61+200×0.66+0.92（x﹣400）≤300， 解得：x≤450． 答：李叔家六月份最多可用电450度． 【考点】二元一次方程组的应用，一元一次不等式的应用 【解析】【分析】（1）观察表格，了解收费标准。抓住已知条件找出等量关系：四月份用电286度，缴纳电费=178.76元；五月份用电316度，缴纳电费=198.56元，建立方程组，解方程即可。 （2此小题的不等关系是：李叔计划六月份电费支出≤300元。根据电费的收费标准设未知数，列不等式，即可求解。 12.【答案】解：如图，过B作BE⊥CD交CD延长线于E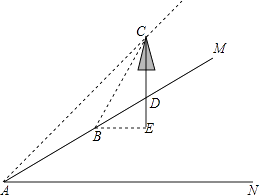，  ∵∠CAN=45°，∠MAN=30°， ∴∠CAB=15° ∵∠CBE=60°，∠DBE=30°， ∴∠CBD=30°， ∵∠CBD=∠CAB+∠ACB， ∴∠CAB=∠ACB=15°， ∴AB=BC=20， 在Rt△BCE中，∠CBE=60°，BC=20， ∴CE=BCsin∠CBE=20×  BE=BCcos∠CBE=20×0.5=10，在Rt△DBE中，∠DBE=30°，BE=10， ∴DE=BEtan∠DBE=10×  ，∴CD=CE﹣DE=  ≈11.5，答：这棵大树CD的高度大约为11.5米． 【考点】特殊角的三角函数值，解直角三角形的应用-仰角俯角问题 【解析】【分析】由在B处，测得树顶端点C的仰角为60°，添加辅助线。过B作BE⊥CD交CD延长线于E，构造直角三角形。先证明△ABC是等腰三角形，然后运用解直角三角形的相关知识，在Rt△BCE、Rt△DBE中分别求出CE、DE的长，即可出树高CD 13.【答案】（1）解：∵抛物线m：y=﹣0.25（x+h）2+k的顶点为M（3，6.25）， ∴m的解析式为y=﹣  （x﹣3）2+  =﹣ （x﹣8）（x+2），∴A（﹣2，0），B（8，0）， ∵将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为D， ∴D的坐标为（13，﹣6.25）， ∴抛物线n的解析式为y= （x﹣13）2﹣ ，即y= x2﹣  x+36（2）解：∵点E与点A关于点B成中心对称， ∴E（18，0）． 设直线DE的解析式为y=kx+b， 则 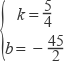 ，解得  ，∴y=  x﹣  ，∵P点的坐标为（x，y），13＜x＜18， ∴S△PEF= PF•OF= x•（﹣y）=﹣ xy=﹣ x（ x﹣ ）=﹣  x2+  x，即S=﹣ x2+ x（13＜x＜18），∴当x=  =9时，S有最大值，但13＜x＜18，所以△PEF的面积S没有最大值；（3）解：直线CM与⊙G相切，理由如下： ∵抛物线m的解析式为y=﹣ （x﹣3）2+ =﹣ （x﹣8）（x+2），∴令x=0，得y=4， ∴C（0，4）． ∵抛物线m的对称轴与x轴的交点为G， ∴G（3，0）， ∵OC=4，OG=3，连结CG， ∴CG=  =5，∵AB=10， ∴⊙G的半径是5， ∴点C在⊙G上． 过M作y轴的垂线，垂足为N，连结CM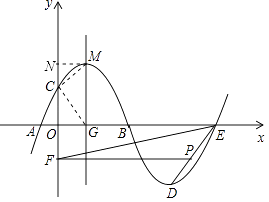，  则CM2=CN2+MN2=（ ﹣4）2+32=  ，又CG2+CM2=52+ =  =（ ）2=GM2 ， ∴CG⊥CM， ∴直线CM与⊙G相切． 【考点】待定系数法求一次函数解析式，二次函数的最值，待定系数法求二次函数解析式，旋转的性质，与二次函数有关的动态几何问题 【解析】【分析】（1）先根据已知条件求出抛物线m的函数解析式。及它与x轴的两交点坐标，再根据旋转的性质，求出旋转后的抛物线的顶点D坐标，即可求出旋转后的抛物线的解析式。 （2）抓住已知过点P作y轴的垂线，可知PF⊥y轴，s= PF•OF，只需用含x的代数式分别表示出PF、OF即可。就要求出直线DE的函数解析式，求出PF、OF的长，就可以表示出s与x的函数关系式，求出此函数的顶点坐标即可。注意x取值范围是13＜x＜18。（3）要判断直线CM与⊙G的位置关系，先要证明点C在⊙G上，根据抛物线m的函数解析式求出点C的坐标，再求出CG的长，可知点C在⊙G上。添加辅助线，连接CG、MC、过点M作y轴的垂线，垂足为N。运用勾股定理分别求出CM2、CG2、GM2 ， 再运用勾股定理的逆定理判断△CMG是否是直角三角形，即可证得直线CM与⊙G相切。 (责任编辑：admin) |