|
☆☆☆ 点击下载试题 ☆☆☆ 由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看! 第Ⅰ 卷(选择题)
一、选择题(本大题共10小题,每小题4分,满分40分) 1.(4分)﹣2017的倒数是( ) A. 2.(4分)地球的表面积约为510000000km2,将510000000用科学记数法表示为( ) A.0.51×109 B.5.1×108 C.5.1×109 D.51×107 3.(4分)下列运算正确的是( ) A.x+y=xy B.2x2﹣x2=1 C.2x•3x=6x D.x2÷x=x 4.(4分)九年级(1)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为:4,6,8,16,16这组数据的中位数、众数分别为( ) A.8,16 B.16,16 C.8,8 D.10,16 5.(4分)下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( ) A. 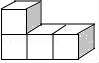 B. B.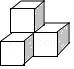 C. C. D. D. 6.(4分)某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( ) A.x(x+1)=1035 B.x(x﹣1)=1035×2 C.x(x﹣1)=1035 D.2x(x+1)=1035 7.(4分)方程组 A.m> 8.(4分)如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( ) 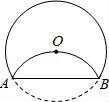 A.2 9.(4分)如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG等于( ) 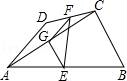 A.47° B.46° C.11.5° D.23° 10.(4分)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形, 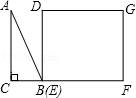 A. 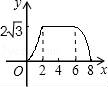 B. B. C. C.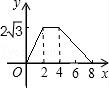 D. D.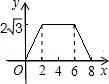 第Ⅱ 卷(非选择题)
二、填空题(本大题共4小题,每小题5分,满分20分) 11.(5分)分解因式:ba2+b+2ab= . 12.(5分)如图,一个圆作滚动运动,它从A位置开始,滚过与它相同的其他六个圆的上部,到达B位置.则该圆共滚过 圈. 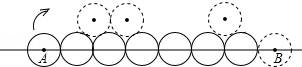 13.(5分)数轴上﹣1所对应的点为A,将A点右移4个单位长度再向左平移6个单位长度,则此时A点距原点的距离为 个单位长度. 14.(5分)如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= 
三、(本大题共2小题,每小题8分,满分16分) 15.(8分)计算:(tan60°)﹣1× 16.(8分)已知x2+x﹣6=0,求
四、解答题(本大题共2小题,每小题8分,满分16分) 17.(8分)两位数相乘:19×11=209,18×12=216,25×25=625,34×36=1224,47×43=2021,… (1)认真观察,分析上述各式中两因数的个位数、十位数分别有什么联系,找出因数与积之间的规律,并用字母表示出来. (2)验证你得到的规律. 18.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2) (1)画出△ABC关于点B成中心对称的图形△A1BC1; (2)以原点O为位似中心,位似比为1:2,在y轴的左侧画出△ABC放大后的图形△A2B2C2,并直接写出C2的坐标. 
五、解答题(本大题共2小题,每小题10分,满分20分) 19.(10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是α,然后在水平地面上向建筑物前进了m米,此时自B处测得建筑物顶部的仰角是β.已知测角仪的高度是n米,请你计算出该建筑物的高度. 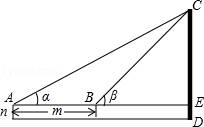 20.(10分)如图,一次函数y=k1x+b与反比例函数y= (1)求一次函数与反比例函数的解析式; (2)根据所给条件,请直接写出不等式k1x+b> (3)若P(p,y1),Q(﹣2,y2)是函数y= 
六、解答题(本大题满分12分) 21.(12分)某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员. (1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率; (2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
七、解答题(本大题满分12分) 22.(12分)如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB. (1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由; (2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长. 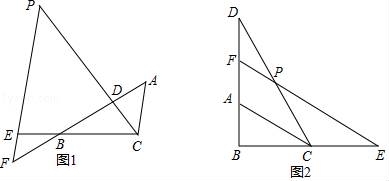
八、(本大题满分14分) 23.(14分)已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示); (2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式; (3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围. 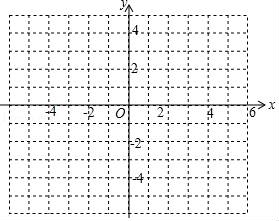 一、选择题(本大题共10小题,每小题4分,满分40分) 1.(4分)﹣2017的倒数是( ) A. 【解答】解:﹣2017的倒数是﹣ 故选:B. 2.(4分)地球的表面积约为510000000km2,将510000000用科学记数法表示为( ) A.0.51×109 B.5.1×108 C.5.1×109 D.51×107 【解答】解:510000000=5.1×108, 故选:B. 3.(4分)下列运算正确的是( ) A.x+y=xy B.2x2﹣x2=1 C.2x•3x=6x D.x2÷x=x 【解答】解:A、x和y不是同类项,不能合并,故本选项错误; B、2x2﹣x2=x2,原式计算错误,故本选项错误; C、2x•3x=6x2,原式计算错误,故本选项错误; D、x2÷x=x,原式计算正确,故本选项正确; 故选:D. 4.(4分)九年级(1)班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为:4,6,8,16,16这组数据的中位数、众数分别为( ) A.8,16 B.16,16 C.8,8 D.10,16 【解答】解:这组数据的中位数为:8, 众数为:16. 故选:A. 5.(4分)下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( ) A. 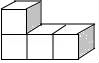 B. B.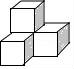 C. C.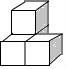 D. D.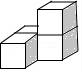 【解答】解:A、左视图是两个正方形,俯视图是三个正方形,不符合题意; B、左视图与俯视图不同,不符合题意; C、左视图与俯视图相同,符合题意; D左视图与俯视图不同,不符合题意, 故选:C. 6.(4分)某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( ) A.x(x+1)=1035 B.x(x﹣1)=1035×2 C.x(x﹣1)=1035 D.2x(x+1)=1035 【解答】解:∵全班有x名同学, ∴每名同学要送出(x﹣1)张; 又∵是互送照片, ∴总共送的张数应该是x(x﹣1)=1035. 故选:C. 7.(4分)方程组 A.m> 【解答】解: 由①得x= ∵x>y,即 故选:D. 8.(4分)如图,将半径为4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )  A.2 【解答】解:如图所示, 连接AO,过O作OD⊥AB,交 ∵ ∴OE=DE, ∵⊙O的半径为4, ∴OE= ∵OD⊥AB, ∴AE= 在Rt△AOE中, AE= ∴AB=2AE=4 故选:B. 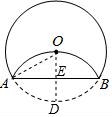 9.(4分)如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点,若∠DAC=20°,∠ACB=66°,则∠FEG等于( ) 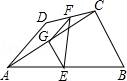 A.47° B.46° C.11.5° D.23° 【解答】解:∵AD=BC,E,F,G分别是AB,CD,AC的中点, ∴GF是△ACD的中位线,GE是△ACB的中位线, 又∵AD=BC, ∴GF=GE,∠FGC=∠DAC=20°,∠AGE=∠ACB=66°, ∴∠FGE=∠FGC+∠EGC=20°+(180°﹣66°)=134°, ∴∠FEG= 故选:D.  10.(4分)如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形, 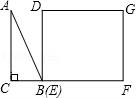 A. 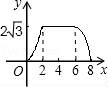 B. B.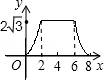 C. C.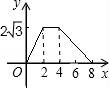 D. D.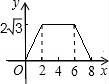 【解答】解:已知∠C=90°,BC=2cm,∠A=30°, ∴AB=4, 由勾股定理得:AC=2 ∵四边形DEFG为矩形,∠C=90, ∴DE=GF=2 ∴AC∥DE, 此题有三种情况:(1)当0<x<2时,AB交DE于H, 如图 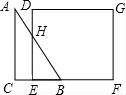 ∵DE∥AC, ∴ 即 解得:EH= 所以y= ∵x y之间是二次函数, 所以所选答案C错误,答案D错误, ∵a= (2)当2≤x≤6时,如图, 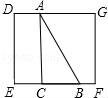 此时y= (3)当6<x≤8时,如图,设△ABC的面积是s1,△FNB的面积是s2, 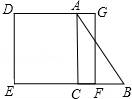 BF=x﹣6,与(1)类同,同法可求FN= ∴y=s1﹣s2, = =﹣ ∵﹣ ∴开口向下, 所以答案A正确,答案B错误, 故选:A. 二、填空题(本大题共4小题,每小题5分,满分20分) 11.(5分)分解因式:ba2+b+2ab= b(a+1)2 . 【解答】解:原式=b(a2+2a+1)=b(a+1)2. 故答案为:b(a+1)2 12.(5分)如图,一个圆作滚动运动,它从A位置开始,滚过与它相同的其他六个圆的上部,到达B位置.则该圆共滚过  【解答】解:观察图1中,当⊙A旋转到⊙A′位置时,∠COD=90°,这个圆已经旋转180°, 即得出结论:⊙A旋转的度数是∠COD的两倍. 第一段和最后一段圆心角为120度.中间一共是4段6圆心角0度的弧,120°×2+60°×4=480度, 480°×2=960°,960°÷360°= 故答案是 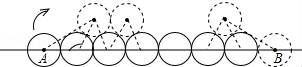 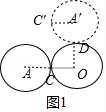 13.(5分)数轴上﹣1所对应的点为A,将A点右移4个单位长度再向左平移6个单位长度,则此时A点距原点的距离为 3 个单位长度. 【解答】解:根据题意:数轴上﹣1所对应的点为A, 将A点右移4个单位长度再向左平移6个单位长度,得到点的坐标为﹣1+4﹣6=﹣3, 故此时A点距原点的距离为3个单位长度. 14.(5分)如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP= 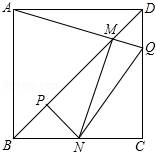 【解答】解:如图1所示: 作AU⊥NQ于U,连接AN,AC, ∵∠AMN=∠ABC=90°, ∴A,B,N,M四点共圆, ∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°, ∴∠ANM=∠NAM=45°, ∴AM=MN,故①正确. 由同角的余角相等知,∠HAM=∠PMN, 在△AHM和△MPN中, 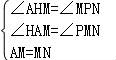 , ,∴△AHM≌△MPN(AAS), ∴MP=AH= ∵∠BAN+∠QAD=∠NAQ=45°, ∴△ADQ绕点A顺时针旋转90度至△ABR,使AD和AB重合,连接AN, 则∠RAQ=90°,△ABR≌△ADQ, ∴AR=AQ,∠RAN=90°﹣45°=45°=∠NAM, 在△△AQN和△ANR中, 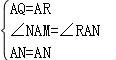 , ,∴△AQN≌△ANR(SAS), ∴NR=NQ, 则BN=NU,DQ=UQ, ∴点U在NQ上,有BN+DQ=QU+UN=NQ,故③正确. 如图2所示,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点, ∴四边形SMWB是正方形, ∴MS=MW=BS=BW,∠SMW=90°, ∴∠AMS=∠NMW, 在△AMS和△NMW中, 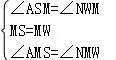 , ,∴△AMS≌△NMW(ASA), ∴AS=NW, ∴AB+BN=SB+BW=2BW, ∵BW:BM=1: ∴ 故答案为:①②③④. 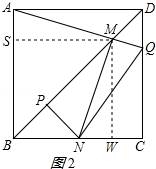 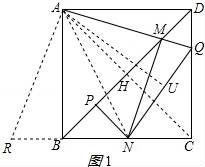 三、(本大题共2小题,每小题8分,满分16分) 15.(8分)计算:(tan60°)﹣1× 【解答】解:原式=( = =1. 16.(8分)已知x2+x﹣6=0,求 【解答】解:x=2或x=﹣3; 原式=( = = = 当x=2时,原式中分母为零,所以x=2舍去; 当x=﹣3时,原式= 四、解答题(本大题共2小题,每小题8分,满分16分) 17.(8分)两位数相乘:19×11=209,18×12=216,25×25=625,34×36=1224,47×43=2021,… (1)认真观察,分析上述各式中两因数的个位数、十位数分别有什么联系,找出因数与积之间的规律,并用字母表示出来. (2)验证你得到的规律. 【解答】解:(1)上述等式的规律是: 两因数的十位数相等,个位数相加等于10,而积后两位是两因数个位数相乘、前两位是十位数乘以(十位数+1); 如果用m表示十位数,n表示个位数的话,则 第一个因数为10m+n,第二个因数为10m+(10﹣n),积为100m(m+1)+n(10﹣n); 表示出来为:(10m+n)[10m+(10﹣n)]=100m(m+1)+n(10﹣n); (2)∵左边=(10m+n)(10m﹣n+10) =(10m+n)[10(m+1)﹣n] =100m(m+1)﹣10mn+10n(m+1)﹣n2 =100m(m+1)﹣10mn+10mn+10n﹣n2 =100m(m+1)+n(10﹣n)=右边 ∴(10m+n)[10m+(10﹣n)]=100m(m+1)+n(10﹣n) 成立. 18.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2) (1)画出△ABC关于点B成中心对称的图形△A1BC1; (2)以原点O为位似中心,位似比为1:2,在y轴的左侧画出△ABC放大后的图形△A2B2C2,并直接写出C2的坐标. 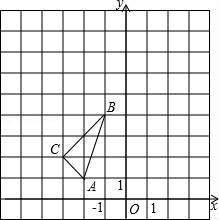 【解答】解:(1)△A1BC1即为所求; (2)△A2B2C2即为所求,C2的坐标为(﹣6,4). 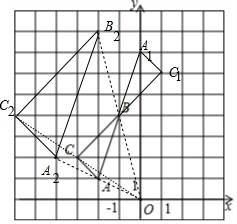 五、解答题(本大题共2小题,每小题10分,满分20分) 19.(10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是α,然后在水平地面上向建筑物前进了m米,此时自B处测得建筑物顶部的仰角是β.已知测角仪的高度是n米,请你计算出该建筑物的高度. 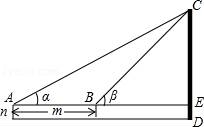 【解答】解:由题意得:BE= ∵AE﹣BE=AB=m米, ∴ ∴CE= ∵DE=n米, ∴CD= ∴该建筑物的高度为:( 20.(10分)如图,一次函数y=k1x+b与反比例函数y= (1)求一次函数与反比例函数的解析式; (2)根据所给条件,请直接写出不等式k1x+b> (3)若P(p,y1),Q(﹣2,y2)是函数y= 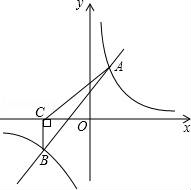 【解答】解:(1)把A(2,m),B(n,﹣2)代入y= 即m=﹣n, 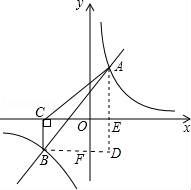 则A(2,﹣n), 过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D, ∵A(2,﹣n),B(n,﹣2), ∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2, ∵S△ABC= ∴ 即A(2,3),B(﹣3,﹣2), 把A(2,3)代入y= 即反比例函数的解析式是y= 把A(2,3),B(﹣3,﹣2)代入y=k1x+b得: 解得:k1=1,b=1, 即一次函数的解析式是y=x+1; (2)∵A(2,3),B(﹣3,﹣2), ∴不等式k1x+b> (3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是P≤﹣2, 当点P在第一象限时,要使y1≥y2,实数p的取值范围是P>0, 即P的取值范围是p≤﹣2或p>0. 六、解答题(本大题满分12分) 21.(12分)某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员. (1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率; (2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率. 【解答】解:(1)∵共有三根细绳,且抽出每根细绳的可能性相同, ∴甲嘉宾从中任意选择一根细绳拉出,恰好抽出细绳AA1的概率是= (2)画树状图: 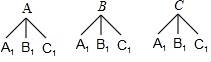 共有9种等可能的结果数,其中甲、乙两位嘉宾能分为同队的结果数为3种情况, 则甲、乙两位嘉宾能分为同队的概率是 七、解答题(本大题满分12分) 22.(12分)如图1,△ABC中,点D在线段AB上,点E在线段CB延长线上,且BE=CD,EP∥AC交直线CD于点P,交直线AB于点F,∠ADP=∠ACB. (1)图1中是否存在与AC相等的线段?若存在,请找出,并加以证明,若不存在,说明理由; (2)若将“点D在线段AB上,点E在线段CB延长线上”改为“点D在线段BA延长线上,点E在线段BC延长线上”,其他条件不变(如图2).当∠ABC=90°,∠BAC=60°,AB=2时,求线段PE的长. 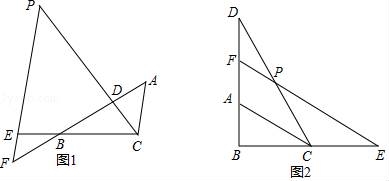 【解答】解:(1)AC=BF.证明如下: 如图1,∵∠ADP=∠ACD+∠A,∠ACB=∠ACD+∠BCD,∠ADP=∠ACB, ∴∠BCD=∠A, 又∵∠CBD=∠ABC, ∴△CBD∽△ABC, ∴ ∵FE∥AC, ∴ 由①②可得, ∵BE=CD, ∴BF=AC; (2)如图2,∵∠ABC=90°,∠BAC=60°, ∴∠ACB=30°=∠ADP, ∴∠BCD=60°,∠ACD=60°﹣30°=30°, ∵PE∥AC, ∴∠E=∠ACB=30°,∠CPE=∠ACD=30°, ∴CP=CE, ∵BE=CD, ∴BC=DP, ∵∠ABC=90°,∠D=30°, ∴BC= ∴DP= 又∵PF∥AC, ∴F是AD的中点, ∴FP是△ADC的中位线, ∴FP= ∵∠ABC=90°,∠ACB=30°, ∴AB= ∴FP=AB=2, ∵DP=CP=BC,CP=CE, ∴BC=CE,即C为BE的中点, 又∵EF∥AC, ∴A为FB的中点, ∴AC是△BEF的中位线, ∴EF=2AC=4AB=8, ∴PE=EF﹣FP=8﹣2=6. 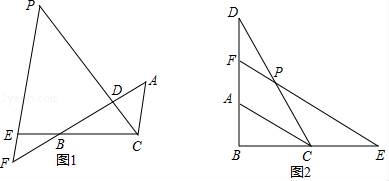 八、(本大题满分14分) 23.(14分)已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示); (2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式; (3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.  【解答】解:(1)∵抛物线y=ax2+ax+b有一个公共点M(1,0), ∴a+a+b=0,即b=﹣2a, ∴y=ax2+ax+b=ax2+ax﹣2a=a(x+ ∴抛物线顶点D的坐标为(﹣ (2)∵直线y=2x+m经过点M(1,0), ∴0=2×1+m,解得m=﹣2, ∴y=2x﹣2, 则 得ax2+(a﹣2)x﹣2a+2=0, ∴(x﹣1)(ax+2a﹣2)=0, 解得x=1或x= ∴N点坐标为( ∵a<b,即a<﹣2a, ∴a<0, 如图1,设抛物线对称轴交直线于点E, ∵抛物线对称轴为x=﹣ ∴E(﹣ ∵M(1,0),N( 设△DMN的面积为S, ∴S=S△DEN+S△DEM= (3)当a=﹣1时, 抛物线的解析式为:y=﹣x2﹣x+2=﹣(x﹣ 有 ﹣x2﹣x+2=﹣2x, 解得:x1=2,x2=﹣1, ∴G(﹣1,2), ∵点G、H关于原点对称, ∴H(1,﹣2), 设直线GH平移后的解析式为:y=﹣2x+t, ﹣x2﹣x+2=﹣2x+t, x2﹣x﹣2+t=0, △=1﹣4(t﹣2)=0, t= (责任编辑:admin) |
