2018年合肥中考数学压轴试题【精选word版含答案解析】_中考网-中考真题答案下载-中考试题库-中考成绩查询-知识点学习方法与技巧补课解题技巧学习计划表总结-中考查分网-中考网-中考资源网-中学学科网

2018年合肥中考数学压轴试题【精选word版含答案解析】
    由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！
    考生注意:本卷共八大题,计23小题,满分150分,考试时间120
    一、选择题(本题共10小题,每题4分,共40分.每小题有四个答,其中有且只有个答案是正确的,请把正确答案的代号,写在题后的括号内,答对的得4分,答错、不答或答案超过一个的一律得0分)
    1.2018的相反数是
    A.-2018   B.2018    C

    2.如图,a∥b,含30°角的三角板的直角顶点在直线b上,一个锐角的顶点在直线a上,
    若∠1=20°,则∠2的度数是
    A.20°   B.40°     C.50°   D.60°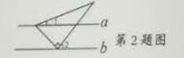
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\W{6YPE{`CV)~9OT9~CNCREX.png$
    3.2017年11月8日-10日,美国总统特朗普对我国进行国事访向,访问期间,中美两国企业签约项目总金额达2500亿美元,这里“2500亿”用科学记数法表示为
    A.2.5×103     B.2.5×1011      C.0.25×1012    D2500×108
    4.如图是由四个大小相同的正方体组成的几何体,它的主视图是
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\A5`HDTUU%7R_KP305CFW5L9.png$
    5.估计

-2的值应该在
A.-1-0之间 B.0-1之间 C.1-2之间 D.2-3之间
6.一元一次不等式组

的解集在数轴上表示正确的是
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\$)BI%DXP%C2L]P7UWUQ[%XR.png$
    17.如图是某班学生篮球运球成绩频数分布直方图,根据图中的信息,这组数据的中位数
    与众数是
    A.10人、20人   B. 13人、14人
    C.14分、14分 D.135分、14分
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\SC(RX77PG%HYQYD$%0EF{W8.png$
    8.如图,一次函数另=-x与二次函数为=ax2+bx+c的图象相交于点M,N,则关于x
    的一元二次方程ax2+(b+1)x+c=0的根的情况是
    A.有两个不相等的实数根    B.有两个相等的实数
    C.没有实数根              D.以上结论都正确
    9.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线AD的延长线交于点E,若点D是弧AC的中点,且∠ABC=70°,则∠AEC等于
    A.80°    B.75°      C.70°     D.65°
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\SLLY8NI08%[97]2J34G1)L4.png$
    10.如图,矩形ABCD中,AB=4,BC=2,把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处,则CD的最小值是
    A.2   B.

二、填空题(本题有4小题,每小题5分,共20分)
11.计算:

=
    12.因式分解:a3-16ab2=
    13.如图,点A,B,C都在⊙O上,∠ACB=60°,⊙O的直径是6,则劣弧AB的长是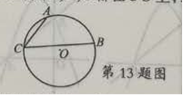
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\}_OF12U7N_~OFVG[5FRV}2Q.png$
    14.在△ABC中,AB=6cm,点P在AB上,且∠ACP=∠B,若点P是AB的三等分点，则AC的长是
               .
    三、(本题有2题,每题8分,共16分)
    15.先化简,再求值:

，其中x=-4
    16.清朝数学家梅文鼎的著作《方程论》中有这样一道题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,
    每亩场地折实田多少?
    译文为:假如有山田3亩,场地6亩,其产粮相当于实田4.7亩;又山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?请你解答
    四、(本题有2题,每题8分,共16分)
    17.已知:如图,一次函数y1=x+2与反比例函数y2=

(x>0)的图象交于点A(a,5)
    (1)确定反比例函数的表达式;
    (2)结合图象,直接写出x为何值时,y1 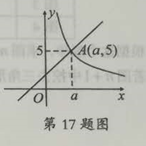    $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\$3ZJUG4SG~`2GZA@T@Y~6KJ.png$
    18.在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
    (1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到
    △A2B2C2;
    (2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\%7]DL}`UNH1A3S2ZEDQ9)_A.png$
    五、(本题有2题,每题10分,共20分)
    19.观察下列图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的
    一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此
    解答下面的问题
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\[_KMH5]6%}Z7@)2S89SD934.png$
    填写下表:

图形	挖去三角形的个数
图形1	1
图形2	1+3
图形3	1+3+9
图形4

    (2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
    (3)若图n+1中挖去三角形的个数为wn+1,求wn+1-Wn
    20.如图,在一座小山上建有一座铁塔AD,小明站在C处测得小山顶A的仰角为30°,
    铁塔顶端的D的仰角为45°,若铁塔AD的高度是100m,试求小山的铅直高度AB(精确到0.1m)(参考数据: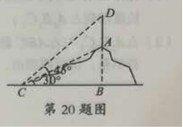

=1.414.

=1.732)
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\Z@B56M_M2PK`YLBTFQ6I8_R.png$
    六、(本题共2分)
    2.小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
    (1)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;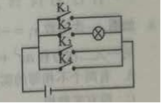
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\OIOPVUQ@L(C{47NX0~2I)A0.png$
    (2)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求同日时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\004FSL~SX@Z[HTU0{~]1{FR.png$
    七、(本题共12分)
    22已知:如图,抛物线y=-x2+bx+C经过点B(0,3)和点A(3,0)
    ()求该抛物线的函数表达式和直线AB的函数表达式;
    (2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\)I(B8DCFQ5C]AO{VSDZWKAO.png$
    八.（本题共14分）
    23.如图，正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),Qp与BC交于E, QP延长线与AD交于点F,连接CQ
    (1)①求证:AP=CQ
    ②求证:PA=AF·AD;
    (2)若AP:PC=1:3,求tan∠CBQ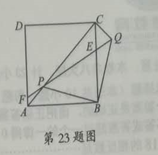
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\MTZ_8TOQDQCB9S316~FAI9Y.png$

2018年合肥中考数学压轴试题参考答案及解析
选择题(本题共10小题,每题4分,共40分.每小题有四个答案,其中有且只有个答案是正确的,请把正确答案的代号,写在题后的括号内)

题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	B	D	A	C	D	A	B	C

    9.B提示:连接OC,∵CE是⊙O的切线,∴∠OCE=900,∵AB是⊙O的直径,
    ∠ACB=90°∴∠BAC=90°-70°=20°∴OA=OC∴∠OAC=∠OCA=20°
    ∵四边形ABCD内接于⊙O,∴∠EDC=∠ABC=70°,∵点D是弧AC的中点,
    ∴∠DAC=∠DCA=

∠EDC=35°
    ∴∠ECD=90°-20°-35°=35°,
    ∴∠AEC=180°-70°-35°=75°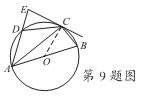
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\F3W3`TCTS%`1QS3BL8_3(ND.png$
    10.C 提示:根据题意,点D’在以点A为圆心,AD为半径且在矩形ABCD内部的圆
    弧上,连接AC交圆弧于点D’,由勾股定理得AC=

,所以CD’
的最小值为

    二、填空题(本题有4小题,每小题5分,共20分)
    11.4
    12.a(a+4b)(a-4b)
    13.

14.

解析:由∠ACP=∠B,∠A=∠A,可得△ACP∽△ABC.

    即AC2=AP·AB.
    分两种情况:
    AP=

AB=2cm,AC2=2×6=12,
AC=

cm;
AP=

AB=4cm,AC2=4×6=24,
AC=

(填对又一个得3分,两个5分)
三、(本题有2题,每题8分,共16分)
15.解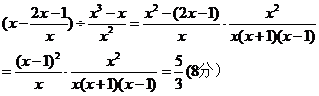

16.解:设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩
可列方程组为

（5分）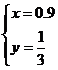
解得

.答:每亩山田相当于实田0.9亩,每亩场地相当于实田

亩.(8分)
    四、(本题有2题,每题8分,共16分)
    17.解
    (1)∵点A(a,5)在一次函数y1=x+2的图象上
    ∴5=a+2,∴a=3,点A坐标为(3,5)
    ∵点A(3,5)在反比例函数

的图象上,∴5=

∴

反比例函数的表达式为y2=

(x>0);(5分)
    (2)由图象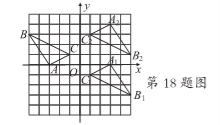可知,当0    18.解
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\7$FH1TV@[45JW8SMPTNRPMG.png$
    (1)如图所示,(5分)
    (2)是,对称中心的坐标是(0,2).(8分)
    五、(本题有2题,每题10分,共20分)
    19.解
    (1)图4挖去三角形的个数为33+32+3+1;(或40)(3分)
    (2)wn=3n-1+3n-2+…+32+3+1;(6分)
    (3)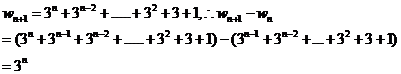

.(10分)
20.解:设AB=x(m),在Rt△ABC中
∵tan30°=

BC=

(3分)
在Rt△BCD中,∵tan45°=

(6分)
∵AD+AB=BD,∴100+x=

x,
    解得x≈136.6(m),(9分)
    答:小山的铅直高度AB约为136.6m.(10分)
    六、(本题共12分
    21.解
    (1)一共有四个开关按键,只有闭合开关按键K2,灯泡才会发光,所以P(灯泡发光)=

    (4分)
    (2)用树状图分析如下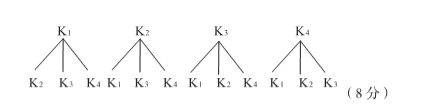
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\PVUP1K%RNPEK~FR1SZQG$BR.png$
    一共有12种不同的情况,其中有6种情况下灯泡能发光,所以P(灯泡发光)

(12分)
    七、(本题共12分)
    (1)∵抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0),

解得

抛物线的函数表达式是y=-x2+2x+3;(2分)
设直线AB:y=kx+m,根据题意得

解得

    ,直线AB的函数表达式是y=-x+3;(4分)
    （2）如图,设直线l的横坐标为a,则点M的坐标为(a,-a2+2a+3),
    点N的坐标是(a,-a+3),又点M,N在第一象限, ∴|MN|=-a2+2a+3-(-a+3)=-a2+3a
    (7分)
    又|MN|=-a2+3a=-(a2-3a+

当a=

时,|MN|有最大值,最大值为

,
即点M与点N之间的距离有最大值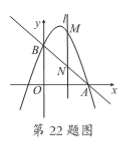

,(10分)
此时点M坐标为(

，

)点N的坐标为

(12分)
     $C:\Users\Administrator\Documents\Tencent Files\532281604\FileRecv\MobileFile\Image\)A2QJE{E1EOYES6$[P(K)2G.png$
    八、(本题共14分)
    23.解
    (1)①∴正方形ABCD,∴AB=CB,∠ABC=90°,∴∠ABP+∠PBC=90°,
    ∵△BPQ是等腰直角三角形,∴BP=BQ,∠PBQ=90°,∴∠PBC+∠CBQ=90°
    ∴∠ABP=∠CBQ,∴△ABP≌△CBQ,∴AP=CQ;(4分)
    ②∵正方形ABCD,∴∠DAC=∠BAC=∠ACB=45°,
    ∵∠PQB=45°,∠CEP=∠QEB,∴∠CBQ=∠CPQ,由①得△ABP≌△CBQ,∠ABP=∠CBQ
    ∵∠CPQ=∠APF,∴∠APF=∠ABP,∴△APF∽△ABP,