|
☆☆☆ 点击下载试题 ☆☆☆ 2018年济南市中考数学模拟测试题【免费版】 由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看! 第I卷(选择题 共60分) 一.选择题(本大题共15个小题,每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.下列立体图形中,俯视图是正方形的是( ) A、 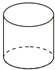 B、 B、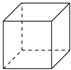 C、 C、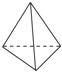 D、 D、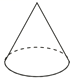 2.将抛物线y=x2先向左平移2个单位,再向 A.y=(x+2)2+2 B.y=(x+2)2﹣2 C.y=(x﹣2)2+2 D.y=(x﹣2)2﹣2[:Z,xx,k.Com] 3.我市药品监察部门为了响应国家解决老百姓看病贵的号召,某药品原价每盒28元,经过连续两次降价,现在售价每盒16元,设该药品平均每次降价的百分率是x,由题意,所列方程正确的是( ) A.28(1﹣2x)=16 B.16(1﹣2x)=28 C.28(1﹣x)2=16 D.16(1﹣x)2=28 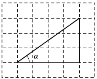 4.反比例函数y=3x的图象在( ) 4.反比例函数y=3x的图象在( )A.第一,三象限 B.第二,四象限 C.第一,二象限 D.第三,四象限 5.三角形在正方形网格纸中的位置如图所示,则sinα的值是( ) A. 6.如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为( ) 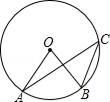 A.35° B.55° C.145° D.70° 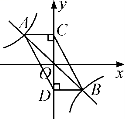 7.如图,函数 7.如图,函数A.2 B.4 C.6 D.8 8.已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( ) A.(﹣3,7) B.(﹣1,7) C.(﹣4,10) D.(0,10) 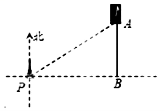 9.如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2 海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )2 9.如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2 海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )2A.2 海里 B.2sin55°海里 C.2cos55°海里 D.2tan55°海里 10.在x2□2xy□y2的空格□中,分别填上“+”或“﹣”,在所得的代数式中,能构成完全平方式的概率是( ) A.1 B. 11.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )  A.4cm B.6cm C.8cm D.2cm[:] 12.关于二次函数y=ax2+bx+c的图象有下列命题: ①当c=0时,函数的图象经过原点; ②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根; ③函数图象最高点的纵坐标是 ④当b=0时,函数的图象关于y轴对称. 其中正确命题的个数是( ) A.1个 B.2个 C.3个 D.4个 第Ⅱ卷(非选择题 共90分) 二、填空题 13.关于x的方程2x2﹣ax+1=0一个根是1,则它的另一个根为 . 14.若 15.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= .  16.已知一个直角三角形的两条直角边的长恰好是方程x2﹣ 17.已知实数x,y满足x2+3x+y﹣3=0,则x+y的最大值为 . 18.在一个暗盒中放有若干个白色球和2 19.如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF =3,则平行四边形ABCD的面积是____________ . [:.Com]  第19题图 第20题图 20.在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线 三、解答题(本大题共7个小题.共66分.解答应写出文字说明、证明过程或演算步骤.) 21.(每小题4分,共8分) (1)计算: (2)在直角三角形ABC中,已知∠C=90°,∠A=60°,BC=3, 22.(本小题8分)某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币. 求:(1)取出纸币的总额是30元的概率; (2)取出纸币的总额可购买一件55元的商品的概率. 23.(本小题8分)如图,某校教学楼 (参考数据:  24.(本小题9分) 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为 A(﹣1,1),B(﹣3,1),C(﹣1,4). (1)画出△ABC关于y轴对称的△A1B1C1;[ (2)将△ABC绕着点B顺时针旋转9  25.(7分)如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°. (1)求∠ABC的度数; (2)求证:AE是⊙O的切线; (3)当BC=4时,求劣弧   26.(本小题9分)如图,已知一次函数 26.(本小题9分)如图,已知一次函数(1)求反比例函数 (2)连结OA,OC,求△AOC的面积. (3)直接写出一次函数值大于反比例函数值的自变量x的 27.(本小题12分)等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小亮拿着30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转. (1)如图1,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP; (2)操作:将三角板绕点P旋转到图2情形时,三角板的两边分别交BA的延长线、边AC于点E、F. ①探究1:△BPE与△CFP还相似吗? ②探究2:连结EF,△BPE与△PFE是否相似?请说明理由; ③设EF=m,△EPF的面积为S,试用m的代数式表示S.  图1 28.(本小题12分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2 (1)求二次函数y=ax2+bx+c的表达式; (2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积; (3)若点M在抛物线上,点N在其对称轴上,使得  (责任编辑:admin) |
