|
☆☆☆ 点击下载试题 ☆☆☆ 2018福州中考数学模拟联考真题【精编Word版免费下载】 由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ (考试时间:120分钟,满分:150分) 友情提示:所有答案都必须写在答题卷上,答在本试卷上无效 一、选择题(共10小题,每题4分,满分40分) 1.下列实数中的无理数是 A.  B.π C.0 D. 2.下面的几何体中,主视图为圆的是  A B C D 3.下列运算正确的是 A.  B. C. D. 4.将一把直尺与一块三角板如图放置,若∠1=55°,则∠2的度数是 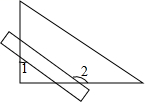 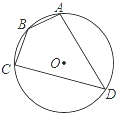 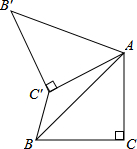 第4题 第7题 第10题 A.145° B.135° C.120 D.115° 5.关于x的一元二次方程  有两个不相等的实数根,则q的取值范围是A.q＞4 B.q＜4 C.q≥4 D.q≤4 6.李华根据演讲比赛中九位评委所给的分数制作了如下表格:
如果要去掉一个最高分和一个最低分,则表中数一定不发生变化的是 A平均数 B.众数 C.中位数 D.方差 7.如图,四边形ABCD是半径为2的⊙O的内接四边形,∠B=135°,则弧AC的长是 A.  B. C.2π D.π8.已知命题“关于x的不等式组  的解集为无解”,说明这个命题是假命题的反例是A.k=3 B.k=-2 C.k=-1 D.k=0 9.已知:不论n为何值,点P(n,4n-5)都在直线  上,若Q(a,b)是直线 上的点则4a-b的值是A.-5 B.-1 C.4 D.5 10.如图,已知△ABC中,∠C=90°，AC=BC=  ,将△ABC绕点A顺时针方向旋转60°到 的位置,连接 ,则的长是A.  B. C. D. 二、填空题(共6小题,每题4分,满分24分) 11.计算:  __________.12.不透明的布袋里有2个黄球、3个红球、4个白球,它们除颜色外其它都相同,那么从布袋中任意摸出一球恰好为红球的概率是_________. 13.如图,为测量出湖边不可直接到达的A、B间的距高,测量人员选取一定点O,使点A、O、C和B、O、D分别在同一直线上,且OB=3OD,OA=30C,量得CD=120米,则AB=_______米. 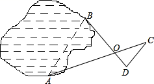 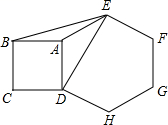 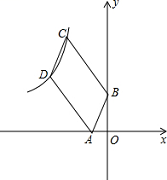 第13题 第15题 第16题 14.已知二次函数  中,函数y与自变量x的部分对应值如下表:
则当y＜10时,x的取值范国是_____________. 15.如图,以正六边形 ADHGFE的一边AD为边向外作正方形ABCD,则∠BED=______. 16.如图,在 平行四边形ABCD中,BC=2AB.A、B两点的坐标分别是(-2,0),(0,4)，C、D两点在反比例函数  (k＜0)的图象上,则k等于________.三、解答题(共9小题,满分86分) 17.(8分)先化简,再求值:  其中 18.(8分)如图,点A、F、C、E在直线  上,AB=D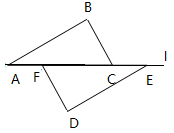E,BC=DF,AF=CE.求证:∠B=∠D  19.(8分)求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。 20.(8分)某商店欲购进一批跳绳,若购进A种跳绳8根和B种跳绳7根,则共需361元；若购进A种跳绳4根和B种跳绳3根,则共需163元。 (1)求A、B两种跳绳的单价各是多少? (2)若该商店准备购进这两种绳共140根,且A种跳绳的数量不少于跳绳总数量的  .若每根A种、B种跳绳的售价分别为27元、33元.问:该商店应如何进货才可获取最大利润,并求出最大利润。 21.(8分)某校为组织代表队参加市“拜炎帝、诵经典”吟诵大亮,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分) A组:75≤x＜80；B组：80≤x＜85；C组:85≤x＜90；D组90≤x＜95；E组:95≤x＜100 并给制出如下两幅不完整的统计图.请根据图中信息,解答下列问题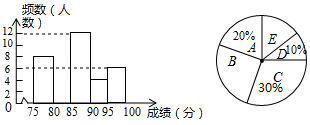：  (1)参加初赛的选手共有____名，扇形统计图中,E组对应的圆心角是_______； (2)现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画 树状图的方法,求恰好选中一名男生和一名女生的概率。 22.(10分)如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线。 (1)作一个⊙O使它经过A、D两点,且圆心O在AB边上(不写作法，保留直线BC与⊙O的位置关系），并说明理由； (2)若AC=5，BC=12求⊙O的半径。  23.(10分)小明在学习直角三角形的三角函数时发现： 如图1,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别是a、b、c， ∵  ∴  ，小明猜想,在锐角三角形中也有相同的结论。(1)如图2,在锐角三角形ABC中,∠A、∠B、∠C所对的边分别是a、b、c，请你运用直角三角形的三角函数的有关知调验证 ；(2)请你运用(1)中的结论完成下题:如图3,在南海某海域一货轮在B处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以80海里/小时的速度按北偏东30°的方向航行,两小时后到达C处,此时又测得灯塔A在货轮的北偏西75°的方向上,求此时货轮与灯塔A的距离。  24.(12分)如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN，延长QN交直线CD于点M. (1)当BQ=1时,求DM的长； (2)过点D作DP⊥CQ于点E,交直线BC于点P,直线QN与直线DP交于点F.当  时,求BQ的长. 25.(14分)已知:点A(a,b)在抛物线  上,一次函数 的图象 经过A.(1)当a=3时,求6m+2n-1的值； (2)若直线  与抛物线只有一个公共点.①求m关于a的函数关系式； ②如果直线  与抛物线的对称轴相交于点B,点P在对称轴上。当BA=PB时,求点P的坐标.(责任编辑：admin) |