|
☆☆☆ 点击下载试题 ☆☆☆ 2018南京中考数学模拟压轴试题【Word版可下载含答案】 由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看! 一、选择题 1.2017上半年,四川货物贸易进出口总值为2 098.7亿元,较去年同期增长59.5%,远高于同期全国19.6%的整体进出口增幅.在“一带一路”倡议下,四川同期对以色列、埃及、罗马尼亚、伊拉克进出口均实现数倍增长.将2098.7亿元用科学记数法表示是( ) A.2.098 7×103 B.2.098 7×1010 C.2.098 7×1011 D.2.098 7×1012
A.  B. B. C. C. D. D. 3.在下列图形中,既是轴对称图形又是中心对称图形的是( )     A B C D 4.下列各式计算正确的是( ) A.(-3x3)2=9x6 B.(a-b)2=a2-b2 C.a3•a2=a6 D.x2+x2=x4 5.某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )A.5 B.6 C.7 D.8 6.如图,在⊙O中,弦AB的长为10,圆周角∠ACB=45°,则这个圆的直径AD为( ) A. 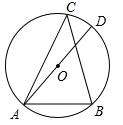 6 6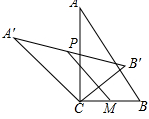 8 87.对于二次函数y=-x2+2x+1的图象与性质,下列说法正确的是( ) A.对称轴是直线x=1,最小值是1 B.对称轴是直线x=1,最大值是1 C.对称轴是直线x=1,最小值是2 D.对称轴是直线x=1,最大值是2 8.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( ) A.4 B.3 C.2 D.1 9.已知点A与点B关于x轴对称,A的坐标是(2,-3),那么经过点B的反比例函数的解析式是( )A. 10.辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整2h后提速行驶至乙地.设行驶时间为x( h),货车的路程为y1( km),小轿车的路程为y2( km ),图中的线段OA与折线OBCD分别表示y1,y2与x之间的函数关系.则以下说法中正确的有( ) ①甲乙两地相距420km;②m=5 ; ③线段CD所在直线的函数表达式: A.1个 B.2个 C.3个 D.4个 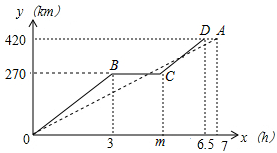 二、填空题 如图,直线AB∥CD,∠BAF=120°,∠E为直角,则cos∠C等于 计算: 13.函数 14.因式分解:-3x2+27= 15. 圆心角为60°,且半径为12的扇形的面积等于 16. 一个不透明布袋里共有5个球(只有颜色不同),其中3个是黑球,2个是白球,从中随机摸出一个球,记下颜色后放回、搅匀,再随机摸出一个球,则两次摸出的球是一黑一白的概率是 17.如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.则灯杆AB的长度是 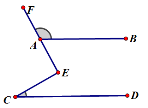 11 11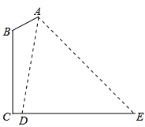 17 17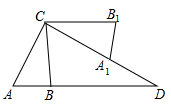 18 1818.如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 19.AC、BD为菱形ABCD的对角线,AB=4,∠ABC=∠ACD,点E在直线BC上,若AE=BD,则CE是 20..如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG= 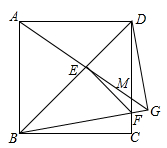 20 20三、解答题 21化简求值: 22.图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上. (1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长; (2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上. 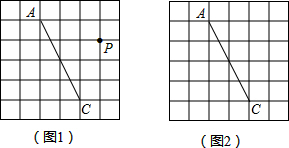 23.某校为了推进学校均衡发展,计划再购进一批图书,丰富学生的课外阅读.为了解学生对课外阅读的需求情况,学校对学生所喜爱的读物:A.文学,B.艺术,C.科普,D.生活,E.其他,进行了随机抽样调查(规定每名学生只能选其中一类读物),并将调查结果绘制成以下不完整的统计图表. 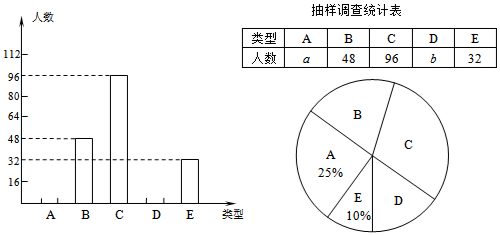 (1)a= ,b= ,请补全条形统计图; (2)如果全校有2500名学生,请你估计全校有多少名学生喜爱科普读物; (3)学校从喜爱科普读物的学生中选拔出2名男生和3名女生,并从中随机抽取2名学生参加科普知识竞赛,请你用树状图或列表法求出恰好抽到一名男生和一名女生的概率. 24.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF. (1)求证:四边形EFGH是菱形; (2)若EF=4,∠HEF=60°,求EG的长. 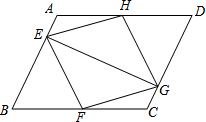  (本题10分)靓丽服装店老板到厂家选期A,B两种型号的服装,A种型号的服装进价比B种型号的服装进价多100元,已知用4500元购进A种型号服装的件数与用3000元购进B种型号服装的件数相同。 (1)求A、B两种型号的服装每件分别为多少元? (2)若A型服装售价每件380元,B型服装售价每件230元,根据市场需求,服装老板决定,购进B型服装的数量要比购进A型服装数量的2倍还多5件,这样服装全部售出后,可使总的获利超过2000元,问至少购进A型型服装多少件? (改编)如图,△ABC内接于⊙O,点D在弧BC上,过点D的切线EF∥BC. (1)如图1,求证:AD平分∠BAC (2)如图2,点H为AD的中点,连接OA,OH,求证:∠AOH=∠ABD; (3)在(2)的条件下,如图3,连接CH.若∠ACH=∠BCH,AB=12,AC=8,求⊙O的半径长 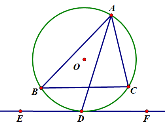 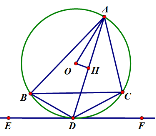 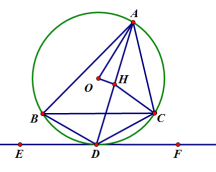
2018南京中考数学模拟压轴试题      (责任编辑:admin) |